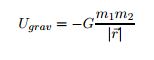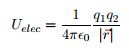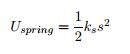The Energy Principle
claimed by Sunil Mutyala
The basis of the energy principle can be described with the statement, "energy can neither be created nor destroyed."
The energy principle is used to describe changes in energy on a system. These energies can take numerous different forms including Kinetic Energy, Potential Energy, Chemical Energy, Rest Energy, and Thermal Energy. The energy principle is a broad equation that can be used to describe the changes in the different types of energy and any work that acts on a system or the transfer of heat into a system. There are many different types of energy, some of which include Kinetic Energy, Potential Energy, Chemical Energy, Rest Energy, Thermal Energy, etc.
The Main Idea
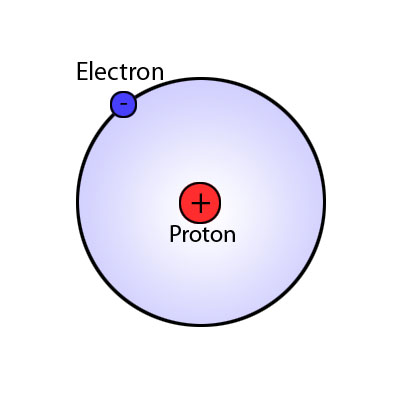
There are many ways to use the energy principle; most of the problems you will encounter will have no work acting on the system and no transfer of heat, thus Esys,initial = Esys,final. Other problems will involve only work acting on the system and no heat. It's important to identify what your system is before making any assumptions about its energy and whether there is any transfer of heat or any work acting on it. It's also useful to note that all objects have rest energy and a object has kinetic energy if it is moving; but, since rest energy is only changed when there is a change in mass of the object, it can usually be disregarded in any calculations. There are also different types of potential energy: Spring Potential Energy, Gravitational Potential Energy, Electric Potential Energy, and Gravitational Potential Energy near the surface of the Earth. Potentially Energy is only included if there is more than one object in your choice of system. For example, a system consisting of one proton and one electron would have Electric Potential Energy. But, a system of an asteroid and Earth would have Gravitational Potential Energy.
For any multi-particle system, you have to take into account the potential energy between each of the objects. It's also key to note that potential energy is zero at very large distances.
Mathematical Models
NOTE: These are a lot of equations, but don't get overwhelmed. You simply have to pick and choose which ones are necessary for the problem given; examples are shown below. For in-depth explanations on each type of energy, look at the associated pages on the Main Page or click on the links in the 'See also' section below.
The Energy Principle
EQ 1: [math]\displaystyle{ {∆E} = {Q + W} }[/math] where [math]\displaystyle{ {Q} }[/math] is heat and [math]\displaystyle{ {W} }[/math] is the amount of work acting on the system.
EQ 2: [math]\displaystyle{ {∆E} = {∆K + ∆E_{Rest} + ∆U + ∆E_{Thermal}} }[/math] - the different types of energy that can be associated with a given particle in a system. Not all have to be present.
EQ 3: [math]\displaystyle{ E_{Rest}=mc^2 }[/math] - Rest Energy, where m is the mass and c is the speed of light.
EQ 4: [math]\displaystyle{ K=\frac{1}{2}mv² }[/math] - Kinetic Energy, where m is the mass and v is the velocity (for speeds less than the speed of light).
EQ 5: [math]\displaystyle{ ∆E_{Thermal} = mC∆T }[/math] - Thermal energy, were m is the mass, C is the specific heat of water (4.2 J/g/K), and T is temperature.
Potential Energy Equations:
A Computational Model
This is a good visualization of kinetic, potential, and total energy.
Examples
Simple
A 1.3 kg book is pushed off a ledge and falls 4.22 m to the ground. What is its kinetic energy the instant that it hits the ground?
Middling
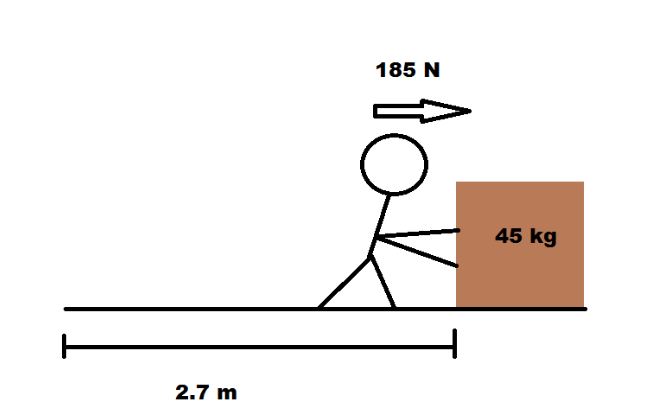
A 45 kg box moves along with a speed of 3.2 m/s. Someone comes up from behind and pushes it for 2.7 m while exerting a force of 185 N. What is the final speed of the box?
Difficult
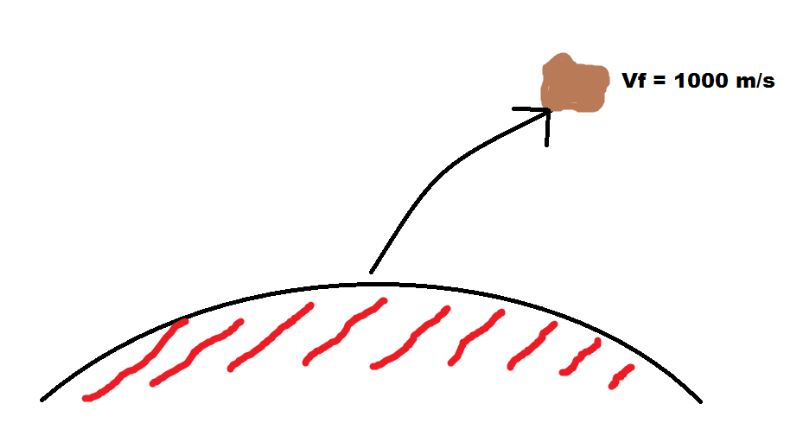
The radius of Mars (from the center to just above the atmosphere) is 3220 km, and its mass is 2 ✕ 10^32 kg. An object is launched straight up from just above the atmosphere of Mars. What initial speed is needed so that when the object is far from Mars its final speed is 1000 m/s?
Connectedness
The Energy Principle can be used for a variety of situations; the fact that it can tell us something about the work acting on a system with only knowing about what energies are present (and vice versa) is what makes this such a fundamental principle. The energy principle is also used to describe the conservation of energy, which is something I find pretty interesting. Energy doesn't just disappear, it's simply converted into a different form. This topic has a huge connection to my major, Biology, because chemical energy (obtained from food) is necessary for a healthy and active body.
History
The concept of energy and its connection to the amount of work performed goes way back to the age of steam engines; physicists and engineers came up with this notion to describe how mechanically and thermally efficient their machines were. In the 1850's, people like William Thomson and William Rankine began to come up with terms like 'kinetic energy' and 'potential energy.' After the 1920's, this study of science became to be known as thermodynamics, the science of energy transformations. This led to the laws of thermodynamics, one of which relates to the conservation of energy.
See also
Potential Energy
Rest Mass Energy
Kinetic Energy
Work
Thermal Energy
Gravitational Potential Energy
Conservation of Energy
Spring Potential Energy
Further reading
Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 6
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/conser.html#coneng
http://hyperphysics.phy-astr.gsu.edu/hbase/enecon.html
References
http://www.texample.net/tikz/examples/earth-orbit/
https://en.wikipedia.org/wiki/Conservation_of_energy
https://en.wikipedia.org/wiki/History_of_energy