Potential Difference Path Independence, claimed by Aditya Mohile

Potential difference is a scalar quantity that measures the difference of electric potential between 2 points. The path taken from one point to another does not affect the potential difference therefore potential difference is said to be path independent.

The Main Idea

The potential difference between two points does not depend on the path taken to get from one point to another because the difference between the locations of the two points remain the same regardless of the path taken to get from one to another.

A Mathematical Model

[math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{l} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]

The potential difference, [math]\displaystyle{ \Delta V_{AB} }[/math], is the integral of the electrical field from point A to point B. This integral, however, is the dot product of [math]\displaystyle{ \vec{E} }[/math] and [math]\displaystyle{ d\vec{l} }[/math] which is equal to the sum of the negative electric field multiplied by the difference of the x,y and z components of the 2 points, as see from the equation above. This proves that the path taken from point A to point B does not matter, only the difference in the positions of points A and B are important in calculating the potential difference.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Problem: Locations A, B, and C are in a region of uniform electric field, as shown in the diagram above. Location A is at < -0.6, 0, 0> m. Location B is at < 0.4, 0, 0>. Location C is at < 0.4, -0.3, 0>m. In the region the electric field = < -750, 400, 0> N/C. Calculate the potential difference between A and C traveling from A to B then to C. Calculate the potential difference traveling from A to C directly.

Step 1

Calculate the displacement vector from A to B.

[math]\displaystyle{ \Delta l = \lt 0.4, 0, 0\gt - \lt -0.6, 0, 0\gt = \lt 1, 0, 0\gt }[/math]

Step 2

Calculate the potential difference between A and B.

[math]\displaystyle{ \Delta V_{AB} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]

[math]\displaystyle{ \Delta V_{AB} = -(-750*1 + 400*0 + 0*0) = 750V }[/math]

Step 3

Calculate the displacement vector from B to C.

[math]\displaystyle{ \Delta l = \lt 0.4, -0.3, 0\gt - \lt 0.4, 0, 0\gt = \lt 0, -0.3, 0\gt }[/math]

Step 4

Calculate the potential difference between B and C.

[math]\displaystyle{ \Delta V_{BC} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]

[math]\displaystyle{ \Delta V_{BC} = -(-750*0 + 400*-0.3 + 0*0) = 120V }[/math]

Step 5

Add [math]\displaystyle{ \Delta V_{AB} }[/math] to [math]\displaystyle{ \Delta V_{BC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]

[math]\displaystyle{ \Delta V_{AC} = \Delta V_{AB} + \Delta V_{BC} = 750 + 120 = 870V }[/math]

Now you have to calculate the potential difference from A to C directly.

Step 1

Calculate the displacement vector from A to C.

[math]\displaystyle{ \Delta l = \lt 0.4, -0.3, 0\gt - \lt -0.6, 0, 0\gt = \lt 1, -0.3, 0\gt }[/math]

Step 2

Calculate the potential difference between A and C.

[math]\displaystyle{ \Delta V_{AB} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]

[math]\displaystyle{ \Delta V_{AB} = -(-750*1 + 400*-0.3 + 0*0) = 750 + 120 = 870V }[/math]

As you can see, potential difference from A to C directly is the same as the potential difference from A to B then to C.

Middling

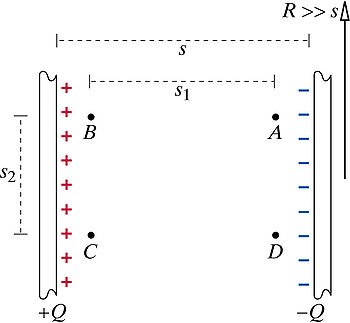
Problem: A capacitor consists of two charged disks of radius 4.7 m separated by a distance s = 2 mm (see the figure). The magnitude of the charge on each disk is 56 µC. Consider points A, B, C, and D inside the capacitor, as shown in the diagram. The distance s1 = 1.5 mm, and the distance s2 = 0.6 mm. (Assume the +x axis is to the right, the +y axis is up, and the +z axis is out.) Find the potential difference between B and D, traveling through A. Find the potential difference from B to D directly. Step 1

Calculate the electric field inside the capacitor.

[math]\displaystyle{ \vec E_{cap} = \frac{Q/A}{\epsilon_{0}} }[/math]

[math]\displaystyle{ \vec E_{cap} = \frac{(56*10^{-6})/(\pi*4.7^{2})}{8.85*10^{-12}} = \lt 91179.912, 0, 0\gt }[/math]

The electric field only has an x-component because the field travels from the positively charged plate to the negatively charged plate, traveling in the +x direction.

Step 2

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

Matter & Interactions volume II by Ruth W. Chabay and Bruce A. Sherwood.