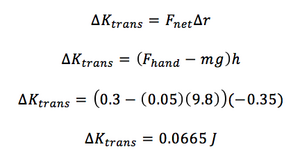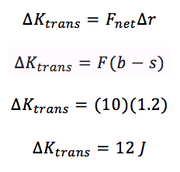Point Particle Systems

The Main Idea

The point particle method of measuring energy change simplifies the system of interest down to a single point or focuses on its center of mass. Instead of looking at the entire system and its individual components, the system is looked at as a single point, with everything else in the surroundings. Thus, the only energy change focused on is the change in kinetic energy, particularly translational kinetic energy. Translational kinetic energy is the energy that comes from an object moving from one location to another, because the only thing that is focused on is the "single particle " system. The extended system, or real system, of the object which includes all energy transfers can later be looked at after looking at the system as a point particle.

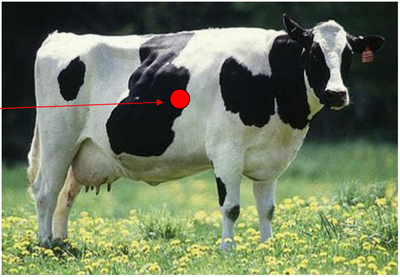Center of Mass of a Cow as a Point

A Mathematical Model

Translational kinetic energy is equal to 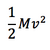, where M is the total mass of the system and v is the velocity of the center of mass.

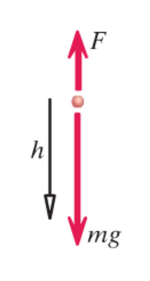
The change in translational kinetic energy is equal to , where F is the net force acting on the object and delta r is the change in position of the object center of mass.

This can also relate back to the idea that translational kinetic energy, delta K is equal to Work in a point particle system. This is why the change in translational energy can be written as the net force times the change in distance of the center of mass.

Another explanation of this is that in the point particle system, total change in energy is equal to the total change in kinetic energy. Because of the energy principle, , where delta E is change in total energy and W is work, the change in translational kinetic energy is thus also equal to work, which is equal to as well.

Examples

Jumper Model

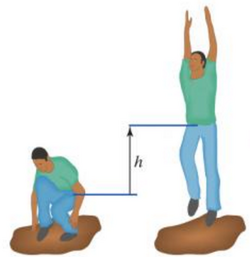
A person jumps straight up in the air from a crouching position. Their center of mass moves h, or 2 m. Their total mass, m is equal to 60 kg. Find the velocity of the center of mass of the jumper. When the jumper jumps, the normal force of the ground is equal to 2x the force of gravity.

Imagine the jumper's center of mass as a point, and it moves up 2 m.

Remember, and . We need to find Fnet. The only forces acting on the jumper are the gravitational force of the Earth and the normal force. Therefore, Fnet = Fn-Fg. Fg = Mg, therefore Fn = 2Mg.

Steps:

When worked out, the v = 6.26 m/s.

The final translational kinetic energy can be used for further calculations if one was to calculate the total change in energy of the real system, including perhaps the thermal energy of the body when jumping increasing, or the rotational kinetic energy of the arms moving.

---

Another example that the point particle system can be applied to is someone hanging motion-less and then jumping down into a crouch position.

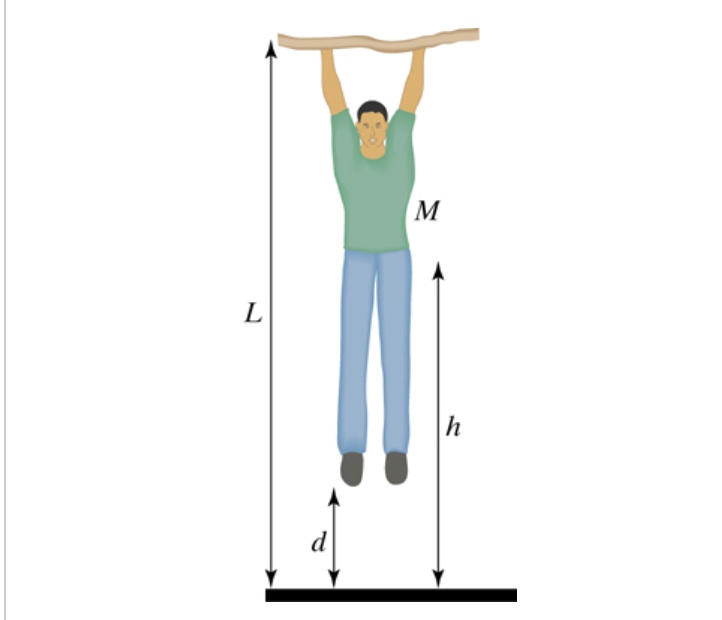
Yo-Yo Example

You pull up on a string the distance d, 0.2 m, with a force, F, 0.3 N. The yo-yo falls a distance h, 0.35 m. The mass of the yo-yo, m, is 0.05 kg. What is the change in translational kinetic energy?

For this example, the Fnet is equal to the force of your hand and the gravitational force of the earth. Delta r is equal to the movement of the yo-yo down, h.

Steps:

This information could be used to solve for the extended system, which would include the work done by your hand and the earth, as well as rotational kinetic energy.

Spring in a Box Example

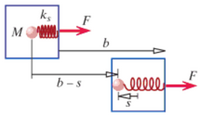
Suppose a thin box contains a ball of clay with the mass M, 2 kg, connected to a relaxed spring, with a stiffness ks, 1.2. The masses of the box and the spring are negligible. It is initally at rest, and then a constant force of F, or 10 N. The box moves a distance b, 1.5 m, and the spring stretches a distance s, 0.3 m, so that the clay sticks to the box. What is the translational kinetic energy of the box?

For the point particle system, the center of mass is the clay because the other masses are negligible. Therefore, delta r is equal to b-s, or 1.2 m. The only force acting on is F in the +x direction.

Steps:

This information could then be used for the extended system. In this example, the extended system would also include the work done by the force F, the potential energy of the spring,as well as any other internal energies.

Connectedness

1. How is this topic connected to something that you are interested in?

I think it is interesting how physicists have simplified the process of finding changes of energy in a system in order to make approximations and calculate more complicated changes in energy. For me, it really helped me to understand exactly what translational kinetic energy is and how it applies to the entire system.

1. How is it connected to your major?

My major is industrial engineering, and although I do not think this topic applies directly to my major, it applies to simplifying and making a more efficient and easy way to calculate the changes of energy in a system. Finding the most efficient way to do something is one of the main goals of industrial engineering, and so in that way, I really enjoy this method of finding changes in energy.

See also

Further reading

For more help, a helpful page is: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real

A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y

External links

See also Real Systems for further information on using Point Particle Systems to solve for the Real Systems.

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.

Yo-yo Clipart: https://www.clipartbest.com