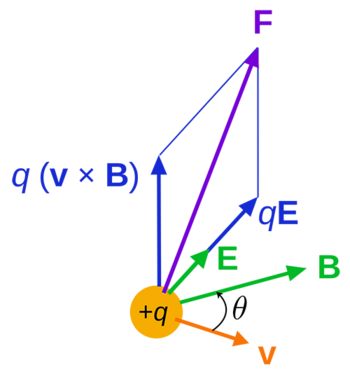
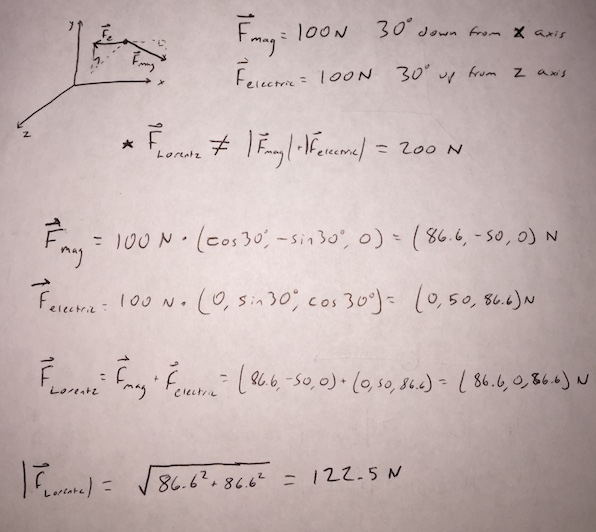Lorentz Force

Claimed by Chris Mickas 11/15/16

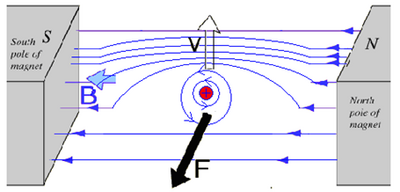
The Main Idea

The Lorentz Force is a name for the sum of the magnetic and electric forces on a particle. The net force on some particles is often primarily determined by the electric and magnetic forces because other forces are negligible. In these cases, the Lorentz Force refers to the net force found by adding the magnetic and electric forces.

A Mathematical Model

[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math] where [math]\displaystyle{ q\vec{E} }[/math] is the electric force and [math]\displaystyle{ q\vec{v} ⨯ \vec{B} }[/math] is the magnetic force.

A Computational Model

Examples

Simple

If the electric force points in the +x direction and the magnetic force points in the –x direction, what direction does the Lorentz force point in?

Solution: More information is needed to know the direction of the force.

Middling

The electric force on a certain particle is <100,-600,300> N and the magnetic force is <-600,400,0> N. Find the Lorentz force.

Solution: Lorentz force = <-500,-200,300> N

Difficult

The magnetic force on a proton is 100 N 30 degrees down from the +x direction. The electric force on the same proton is 100 N 30 degrees up from the +z direction. What is the magnitude of the Lorentz Force on the proton?

Solution: Lorentz force = 122.5 N

Connectedness

I'm very interested in music and sound amplification. Speakers use the Lorentz force of an electromagnet to move a cone that creates sound waves in the air. When current flows through the wires in the electromagnetic in different quantities, the speakers move in unique ways to produce the different sounds that we recognize. Amplifiers for electric guitars and basses work in the same way. As a guitar player, I'm interested by the physics of how electric guitars work.

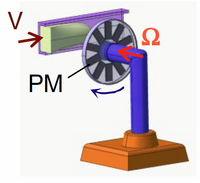
2. One of my areas of interest as a mechanical engineering student is sustainable and renewable energy. Wind turbines and hydropower plants both work by harnessing the kinetic energy of water or wind and using it to induce an electrical current. The turbines rotate and move a permanent magnet that induces a current in an electromagnet placed inside of the magnet, which is shaped like a hollow cylinder. The induced current is then carried via wires to external sources to provide energy.

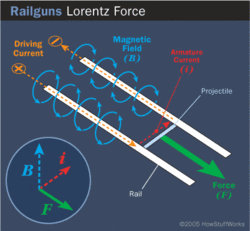
3. Several industries manufacture products that induce current using the Lorentz Force. For example, electric guitars and basses work by magnetizing the strings and relying on the Lorentz force to create a current in pickups that is then transmitted to an amplifier. Pickups are small electromagnet coils surrounding a magnet that are placed beneath the strings. The strings become magnetized because of the magnet inside the pickup. When they are played and vibrate, they induce current in the electromagnet. The Lorentz force causes the strings to exert forces that move mobile charges and induce the current. The current is then increased through a potentiometer and sent to an amplifier through a cable.

History

Early attempts to quantitatively describe the electromagnetic force were made in the mid-18th century. It was proposed that the force on magnetic poles, by Johann Tobias Mayer and others in 1760, and electrically charged objects, by Henry Cavendish in 1762, obeyed an inverse-square law. However, in both cases the experimental proof was neither complete nor conclusive. It was not until 1784 when Charles de Coulomb, using a torsion balance, was able to definitively show through experiment that this was true. Soon after the discovery in 1820 by Hans Christian Ørsted that a magnetic needle is acted on by a voltaic current, Andre Marie Ampere that same year was able to devise through experimentation the formula for the angular dependence of the force between two current elements. In all these descriptions, the force was always given in terms of the properties of the objects involved and the distances between them rather than in terms of electric and magnetic fields.

The modern concept of electric and magnetic fields first arose in the theories of Michael Faraday, particularly his idea of lines of force, later to be given full mathematical description by William Thomson (Lord Kelvin) and James Maxwell. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, in the time of Maxwell it was not evident how his equations related to the forces on moving charged objects. J.J. Thomson was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as [math]\displaystyle{ \vec{F} = q\vec{E} + \frac{q}{2}\vec{v} ⨯ \vec{B} }[/math].

Although some historians suggest that the Lorentz force originated in the works of Maxwell, the first derivation is generally attributed to Oliver Heaviside in 1889. The Lorentz force's namesake is attributed to Hendrik Lorentz, who derived it a few years after Heaviside.

Feynman, Richard Phillips; Leighton, Robert B.; Sands, Matthew L. (2006). The Feynman lectures on physics (3 vol.). Pearson / Addison-Wesley. ISBN 0-8053-9047-2.: volume 2.
Jackson, John David (1999). Classical electrodynamics (3rd ed.). New York, [NY.]: Wiley. ISBN 0-471-30932-X.
Serway, Raymond A.; Jewett, John W., Jr. (2004). Physics for scientists and engineers, with modern physics. Belmont, [CA.]: Thomson Brooks/Cole. ISBN 0-534-40846-X.

Lorentz Force

Contents

The Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

See also

Further reading

External links

References

Navigation menu