Potential Difference Path Independence, claimed by Aditya Mohile
Claimed by Aditya Mohile
Claimed by Zachary Wright (Fall 2016)
Potential difference or Voltage is a scalar quantity that measures the difference of electric potential energy between two points. Potential energy differences depend only on final and initial states and is independent of the path taken to arrive at those states. Likewise, the potential difference between a final and initial state is independent of the path taken to arrive at those states, therefore the potential difference is said to be path independent. The units of measurement for potential difference is joules per coulomb, which is equal to volts.
The Main Idea
The potential difference between two points does not depend on the path taken to get from one point to another because the difference between the locations of the two points remains the same regardless of the path taken to get from one point to another.
A Mathematical Model
- [math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{l} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
The potential difference, [math]\displaystyle{ \Delta V_{AB} }[/math], is the integral of the electrical field from point A to point B. This integral, however, is the dot product of [math]\displaystyle{ \vec{E} }[/math] and [math]\displaystyle{ d\vec{l} }[/math] which is equal to the sum of the negative electric field multiplied by the difference of the x,y and z components of the two points, as see from the equation above. This proves that the path taken from point A to point B does not matter, only the difference in the positions of points A and B are important in calculating the potential difference.
As shown above, the potential difference between points A and B in the electric field E is independent of the path.
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple

Problem: Locations A, B, and C are in a region of uniform electric field, as shown in the diagram above. Location A is at < -0.6, 0, 0> m. Location B is at < 0.4, 0, 0>. Location C is at < 0.4, -0.3, 0>m. In the region the electric field = < -750, 400, 0> N/C. Calculate the potential difference between A and C traveling from A to B then to C. Calculate the potential difference traveling from A to C directly.
Step 1
- Calculate the displacement vector from A to B.
- [math]\displaystyle{ \Delta l = \lt 0.4, 0, 0\gt - \lt -0.6, 0, 0\gt = \lt 1, 0, 0\gt }[/math]
Step 2
- Calculate the potential difference between A and B.
- [math]\displaystyle{ \Delta V_{AB} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AB} = -(-750*1 + 400*0 + 0*0) = 750V }[/math]
Step 3
- Calculate the displacement vector from B to C.
- [math]\displaystyle{ \Delta l = \lt 0.4, -0.3, 0\gt - \lt 0.4, 0, 0\gt = \lt 0, -0.3, 0\gt }[/math]
Step 4
- Calculate the potential difference between B and C.
- [math]\displaystyle{ \Delta V_{BC} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{BC} = -(-750*0 + 400*-0.3 + 0*0) = 120V }[/math]
Step 5
- Add [math]\displaystyle{ \Delta V_{AB} }[/math] to [math]\displaystyle{ \Delta V_{BC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]
- [math]\displaystyle{ \Delta V_{AC} = \Delta V_{AB} + \Delta V_{BC} = 750 + 120 = 870V }[/math]
Now you have to calculate the potential difference from A to C directly.
Step 1
- Calculate the displacement vector from A to C.
- [math]\displaystyle{ \Delta l = \lt 0.4, -0.3, 0\gt - \lt -0.6, 0, 0\gt = \lt 1, -0.3, 0\gt }[/math]
Step 2
- Calculate the potential difference between A and C.
- [math]\displaystyle{ \Delta V_{AB} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AB} = -(-750*1 + 400*-0.3 + 0*0) = 750 + 120 = 870V }[/math]
As you can see, potential difference from A to C directly is the same as the potential difference from A to B then to C.
Middling
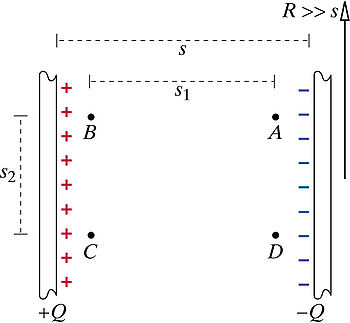
Problem: A capacitor consists of two charged disks of radius 4.7 m separated by a distance s = 2 mm (see the figure). The magnitude of the charge on each disk is 56 µC. Consider points A, B, C, and D inside the capacitor, as shown in the diagram. The distance s1 = 1.5 mm, and the distance s2 = 0.6 mm. (Assume the +x axis is to the right, the +y axis is up, and the +z axis is out.) Find the potential difference between B and D, traveling through A. Find the potential difference from B to D directly. Step 1
- Calculate the electric field inside the capacitor.
- [math]\displaystyle{ \vec E_{cap} = \frac{Q/A}{\epsilon_{0}} }[/math]
- [math]\displaystyle{ \vec E_{cap} = \frac{(56*10^{-6})/(\pi*4.7^{2})}{8.85*10^{-12}} = \lt 91179.912, 0, 0\gt }[/math]
The electric field only has an x-component because the field travels from the positively charged plate to the negatively charged plate, traveling in the +x direction.
Step 2
- Calculate the displacement vector from B to A.
- Set the origin at B.
- [math]\displaystyle{ \Delta l = \lt s_{1}, 0, 0\gt - \lt 0, 0, 0\gt = \lt s_{1}, 0, 0\gt = \lt 0.0015, 0, 0\gt }[/math]
Step 3
- Calculate the potential difference between B and A.
- [math]\displaystyle{ \Delta V_{BA} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{BA} = -(91179.912*0.0015 + 0*0 + 0*0) = -136.770V }[/math]
Step 4
- Calculate the displacement vector from A to D
- [math]\displaystyle{ \Delta l = \lt s_{1}, s_{2}, 0\gt - \lt s_{1}, 0, 0\gt = \lt 0, s_{2}, 0\gt = \lt 0, s_{2}, 0\gt = \lt 0, 0.006, 0\gt }[/math]
Step 5
- Calculate the potential difference between A and D.
- [math]\displaystyle{ \Delta V_{AD} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AD} = -(91179.912*0 + 0*0 + 0*0) = 0V }[/math]
Step 6
- Add [math]\displaystyle{ \Delta V_{BA} }[/math] to [math]\displaystyle{ \Delta V_{AD} }[/math] to get [math]\displaystyle{ \Delta V_{BD} }[/math]
- [math]\displaystyle{ \Delta V_{BD} = \Delta V_{BA} + \Delta V_{AD} = -136.770 + 0 = -136.770V }[/math]
Notice that the voltage is negative since we are going from the positively charged plate (high potential) to the negatively charged plate (low potential) losing potential energy in the process.
Now you have to calculate the potential difference from A to C directly.
Step 1
- Calculate the displacement vector from B to D.
- [math]\displaystyle{ \Delta l = \lt s_{1}, s_{2}, 0\gt - \lt 0, 0, 0\gt = \lt s_{1}, s_{2}, 0\gt = \lt s_{1}, s_{2}, 0\gt = \lt 0.0015, 0.006, 0\gt }[/math]
Step 2
- Calculate the potential difference between B and D.
- [math]\displaystyle{ \Delta V_{AD} = -(E_{x}\Delta x + E_{y}\Delta y + E_{z}\Delta z) }[/math]
- [math]\displaystyle{ \Delta V_{AD} = -(91179.912*0.0015 + 0*0 + 0*0) = -136.770V }[/math]
Notice that potential difference traveling from B to A then D is the same as the potential difference traveling from B to D directly. This exemplifies that the potential difference does not depend on the path taken to get from one point to another.
Difficult
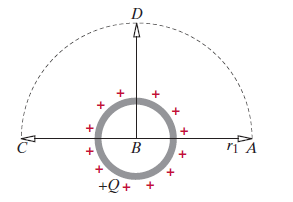
Problem: A uniform spherical shell of charge +Q is centered at point B, as shown in the figure below. Show that ΔV = VC − VA is independent of path by calculating ΔV for each of these two paths (actually do the integrals). (Use the following as necessary: Q, R for the radius of the spherical shell, r1 for the radius of the circular arc A → D → C with B at its center, and ε0.)
Step 1
- Calculate the potential difference from A to C following the path A → B → C.
- First, calculate the potential difference from A to B.
- [math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{l} }[/math]
- In order to calculate the potential difference from A to B, calculate the electric field of the sphere.
- [math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} }[/math]
- Now plug the electric field calculated above into the integral and solve.
- [math]\displaystyle{ \Delta V_{AB} = \int_{A}^{B} \vec{E} \cdot d\vec{r} = \int_{r_{1}}^{R} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{R^{2}} - \frac{Q}{r_{1}^{2}}) }[/math]
- Now calculate the potential difference from B to C.
- Use the electric field of the sphere calculated above to solve the below integral.
- [math]\displaystyle{ \Delta V_{BC} = \int_{B}^{C} \vec{E} \cdot d\vec{l} }[/math]
- [math]\displaystyle{ \Delta V_{BC} = \int_{R}^{r_{1}} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{R^{2}}) }[/math]
- Now add [math]\displaystyle{ \Delta V_{AB} }[/math] to [math]\displaystyle{ \Delta V_{BC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]
- [math]\displaystyle{ \Delta V_{AC} = \Delta V_{AB} + \Delta V_{BC} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{R^{2}} - \frac{Q}{r_{1}^{2}}) + \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{R^{2}}) = 0V }[/math]
Step 2
- Calculate the potential difference from A to C following the path A → D → C.
- First calculate the potential difference from A to D.
- [math]\displaystyle{ \Delta V_{AD} = \int_{A}^{D} \vec{E} \cdot d\vec{l} }[/math]
- Use the same electric field of the sphere calculated in step 1, shown below.
- [math]\displaystyle{ \vec{E}_{sphere} = \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} }[/math]
- Now plug the electric field calculated above into the integral and solve.
- [math]\displaystyle{ \Delta V_{AD} = \int_{A}^{D} \vec{E} \cdot d\vec{r} = \int_{r_{1}}^{r_{1}} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) = 0V }[/math]
- Now calculate the potential difference from D to C.
- Use the electric field of the sphere calculated above to solve the below integral.
- [math]\displaystyle{ \Delta V_{DC} = \int_{D}^{C} \vec{E} \cdot d\vec{l} }[/math]
- [math]\displaystyle{ \Delta V_{DC} = \int_{r_{1}}^{r_{1}} \frac{1}{4\pi\epsilon_{0}}\frac{Q}{r^{2}} \cdot d\vec{r} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) }[/math]
- Now add [math]\displaystyle{ \Delta V_{AD} }[/math] to [math]\displaystyle{ \Delta V_{DC} }[/math] to get [math]\displaystyle{ \Delta V_{AC} }[/math]
- [math]\displaystyle{ \Delta V_{AC} = \Delta V_{AD} + \Delta V_{DC} = \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) + \frac{1}{4\pi\epsilon_{0}}(\frac{Q}{r_{1}^{2}} - \frac{Q}{r_{1}^{2}}) = 0V }[/math]
- Notice that either path taken from A to C results in the same potential difference of 0V.
Connectedness
- How is this topic connected to something that you are interested in?
- I am very interested in electronics and circuitry so knowing that potential difference is path independent definitely helps in determining the voltage between 2 points in a complicated circuit with many paths.
- How is it connected to your major?
- I am an electrical engineering major so this knowledge is very applicable to determining the voltage between 2 points in a circuit that contains many loops or is very complex.
- In Circuits
- Path Independence of potential difference is critical in solving circuit equations. Many values in a circuit can be calculated using these principles and the Kirchoff's Voltage Law.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why. Luigi Galvani, an Italian physicist, discovered something he called "animal electricity" which was two different metals connected in series with a frog leg and each other. However, Alessandro Volta, another Italian physicist, realized that the frog leg was acting as a conductor and a detector of electricity, or an electrolyte. He later replaced the frog leg with brine soaked paper and noticed the same results. Through this, Volta discovered electromotive force relating to a galvanic cell, realizing that the difference between the two electrode potentials caused electricity to flow.
See also
https://en.wikipedia.org/wiki/Voltage
Further reading
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elewor.html#c2
External links
References
Matter & Interactions volume II by Ruth W. Chabay and Bruce A. Sherwood.
