Bohr Model

Sherry Guo (Spring 2017)

This page gives basic information about the Bohr Model and Quantization. It also includes examples using Bohr Model.

Main Idea

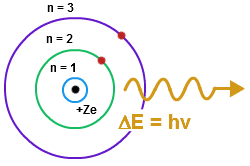
The Bohr model of the atom was proposed by Niels Bohr in 1913, and it was radically different from any other models that previously existed. His model depicted atoms as having negatively charged electrons which orbited as small, positively charged nucleus. Bohr's incorporation of quantum theory was the most groundbreaking part; in this model, electrons can only exist in discrete energy levels, which are quantized. This model is very simplistic and is useful in introducing students to quantum mechanics. Although this model successfully predicts energy levels of the hydrogen atom, it has its shortcomings.

A Mathematical Model

This model gives us the formula for the radius derived from translational angular momentum.

|Ltrans,nucleus| = Nh* where N = 1,2,3

Note: h* is used when is not the actual notation for it.

h* = h/2π = 1.05 * 10^-34 J*s

1) |Ltrans,nucleus| = Nh*,rp = Nh*

2) From curving motion: [math]\displaystyle{ |Fperpendicular| = {\frac{|p| |v|}{r}} = {\frac{e^2}{4π ε0 r^2}} }[/math]

3) Substitute in Bohr's Condition: [math]\displaystyle{ {\frac{N^2 h*^2}{mr^3}} = {\frac{e^2}{4π ε0 r^2}} }[/math]

4) Solve for the Radius [math]\displaystyle{ r = {\frac{4π ε0 h*^2}{me^2}} *N^2 }[/math] where N = 1,2,3

Thus Bohr's Model derives equation for the radius.

Additionally, the formula for energy of hydrogen atom of different levels is also derived from this model.

E = K + Uelectric

1) [math]\displaystyle{ E = {\frac{mv^2}{2}} - {\frac{{\frac{1}{2}}*{\frac{1}{4π ε0}}*{\frac{me^2}{h*}}}{N^2}} }[/math]

2) [math]\displaystyle{ E = {\frac{13.6 eV}{N^2}} }[/math] where N = 1,2,3

A Computational Model

To interact with this glowscript visualization of the Bohr Model, click here. You will also find a graph of Energy (eV), Kinetic Energy, and Potential Energy. This visualization shows how the electrons jump from level to level according to the Bohr Model. There is also an energy vs distance graph shown which varies according to these levels. Notice that the further away the electron is, the more energy it has.

Examples

Simple

How much energy in electron volts is required to ionize a hydrogen atom, if initially the atom is in the state N = 3? Here we can use the formula for the hydrogen atom which is

1) [math]\displaystyle{ E = {\frac{-13.6 eV}{N^2}} }[/math]

2) [math]\displaystyle{ ={\frac{-13.6 eV}{3^2}} }[/math] = -1.51 Joules

Middling

[6]A hydrogen atom is in state N = 3, where N = 1 is the lowest energy state. What is K+U in electron volts for this atomic hydrogen energy state?

1) [math]\displaystyle{ E(3) = {\frac{-13.6 eV}{3^2}} }[/math] = -1.51 Joules

2) [math]\displaystyle{ E(1) = {\frac{-13.6 eV}{1^2}} }[/math] = -13.6 Joules

3) K+U = energy of photon = [math]\displaystyle{ E(1) - E(3) = {\frac{-13.6 eV}{3^2}} - {\frac{-13.6 eV}{1^2}} }[/math] = 12.09 Joules

To the right is the graph of E as the hydrogen atom goes from N = 3 to N = 1.

Difficult

Hydrogen has been detected transitioning from the 101^st to the 100^th energy levels. What is the wavelength of the radiation? Where in the electromagnetic spectrum is this emission?

To solve this problem, we first need to use formulas derived from Bohr Model of hydrogen atom. It is [math]\displaystyle{ E = {\frac{-13.6 eV}{N^2}} }[/math]

Then solve for the wavelength using formula from Electromagnetic Wave Theory.

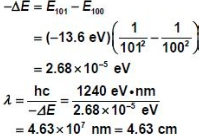
This wavelength falls in the microwave portion of the electromagnetic spectrum.

Connectedness

This topic is quite interesting as it is the initial introduction to quantum physics, which I find particularly intriguing. Although, this model has had shortcomings, it is one of the most successful models of its time. It has many features that are used in the actual model for quantum physics. This model also involves coding to show the visualization, which is how it somewhat related to Computer Science. Additionally, there are quite a few applications of the Bohr's Model. Bohr's discovery of the quantum leap is, in many ways, the most shining example of the consequences which Bohr's model of the atom has had for modern society. Bohr's notion that atoms emit light quanta with very specific energies is behind many of the technologies on which we depend our daily lives. Laser technology, which is becoming very popular in today's world, depends entirely on principles behind Bohr's model of atom because laser light is produced by quantum leaps. The quantum leaps between the specific energy levels show that light has specific frequency and wavelength which measures time and length precisely. However, due to shortcomings in Bohr's Model, we can't completely utilize these calculations, but the framework is used.

History

Ernest Rutherford proposed that the basic structure of an atom is a cloud of electrons which surround a small nucleus. With his experiments, he developed a model that depicted an atom like a solar system, with electrons orbiting around the nucleus. However, his proposal was flawed, as it suggested all atoms are unstable and can emit energy that isn't quantized. [8]

Niels Bohr was able to explain the emission spectra of hydrogen by improving on the Rutherford model of the atom. Bohr’s model improved the classical atomic models of physicists J. J. Thomson and Ernest Rutherford by incorporating quantum theory. While working on his doctoral dissertation at Copenhagen University, Bohr studied physicist Max Planck’s quantum theory of radiation. Then after graduating, Bohr worked in England with Thomson and subsequently with Rutherford to come up with this model. During this time, Bohr developed his model of atomic structure. Initially, Rutherford's planetary model predicted a continuous spectrum of light from hydrogen. However, Bohr corrected for this by proposing that the translational angular momentum of the electron can be quantized. Although this model is not entirely correct, as it only applies to systems where two charged particles orbit each other, it still has many features that are very applicable to physics today.

Shortcomings of the Bohr Model

The Bohr Model is an important predecessor to the current quantum mechanical models of the atom. However, there are some characteristics of the Bohr model that are not entirely correct. The actual quantization rules in a hydrogen atom are much more complex than those assumed in the Bohr Model. The translational angular momentum in ground state (N = 1), is zero, not h, and for the next higher state of N = 2, the z component of translational angular momentum can either be zero or h. Other issues with the Bohr Model include that it violates the Heisenberg Uncertainty Principle because it considers electrons to have both a known radius and orbit. It also makes poor predictions regarding spectra of larger atoms, and does not predict the relative intensities of spectral lines.

[1] [2] [3] [4] [5] [6] [7] [8]

Bohr Model

Contents

Main Idea

A Mathematical Model

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

History

Shortcomings of the Bohr Model

See also

Further reading

External links

References

Navigation menu