Gauss's Flux Theorem

Claimed by Marian Mitchell (SPRING 2017)

This is a page about Gauss's Flux Theorem. A work in progress by Jeff Patz

The Main Idea

Gauss's Flux Theorem is a way of relating charge distribution inside of a closed surface to its resulting electric field. Analyzing the direction and magnitude of the electric field present on a closed surface helps in understanding the total sum of the charge on the inside of the closed surface. The mathematical model (as shown below) used to related electric field and charge distribution displays that there is a proportional relationship between the amount of electric field passing through a surface and the amount of charge inside of the surface. This application of Gauss's Flux Theorem can be applied to a surface with any shape and size. Since Gauss's Law uses the superposition principle in order to find the sum of all of the charges inside of a closed surface, charges present on the outside of the surface contribute no net flux and produce no electric field on the surface of the object.

A Mathematical Model

In words, the electric flux of a closed surface is equal to the total charge enclosed in the closed surface over the constant epsilon naught. The electric flux of a closed surface is also equal to the surface integral of the electric field evaluated over the closed surface.

[math]\displaystyle{ \Phi_E = \frac{\Sigma q}{\varepsilon_0} = \oint_C E\bullet \hat{n} dA }[/math]

Where E is the electric field, dA is the infinitesimal area in the direction of the electric field, [math]\displaystyle{ \hat{n} }[/math] is the unit normal vector, sigma q is the sum of the charges inside the closed surface, and the dot denotes a dot product.

For the special case of a constant electric field, the electric flux is equal to the electric field over the closed surface multiplied by the area and the cosine of the angle between the two vectors.

[math]\displaystyle{ \Phi_E = EAcos(\theta) }[/math]

Where E is the electric field, A is area of the surface, and [math]\displaystyle{ \theta }[/math] is the angle between the E and A

A Computational Model

Gauss's Flux Theorem is able to be visualized by observing the direction and angle of an electric field traveling through a given surface.

Examples

Easy

One Surface and Uniform Electric Field

A disk of radius 5 centimeters is in an area of uniform electric field with magnitude 400 Volts/Meter. The angle between the electric field and the disk is 35 degrees.

Using the simplified version of Gauss's Law because the electric field is uniform: [math]\displaystyle{ \Phi_E = EAcos(\theta) }[/math], fill out the known values, which in the case is all values needed.

[math]\displaystyle{ \Phi_E = (400)(\pi0.05^2)cos(35) }[/math]

[math]\displaystyle{ \Phi_E = 2.573 }[/math] Volt Meters

Middling

Multiple Surfaces and Uniform Electric field

An equilateral prism lies on top of a rectangular prism with dimensions l = 5cm, w = 7cm, h = 19cm, and is in an area of uniform electric field with magnitude 560 Volts/Meter perpendicular to the long sides of the rectangular prism.

Using the simplified version of Gauss's Law because the electric field is uniform: [math]\displaystyle{ \Phi_E = EAcos(\theta) }[/math]

First of all it is important to note that there are four surfaces that contribute to the net electric flux. two of the two long sides of the equilateral prism and two of the long sides of the rectangular prism. We know the angles between E and A because the top prism is an equilateral triangle, so all the side angles are 60 degrees. With this equation we can write:

[math]\displaystyle{ \Phi_E = E[(w*h)cos(120) + (w*h)cos(60) + (w*h)cos(180) + (w*h)cos(0)] }[/math]

[math]\displaystyle{ \Phi_E = 0 }[/math]

Difficult

Non-Uniform Electric Field

A solid sphere of radius R has a charge +Q uniformly distributed throughout. Find the Electric field at locations r1<R, r2>R.

For this problem we can utilize the equality of [math]\displaystyle{ \frac{Q}{\varepsilon_0} = \oint_C E\bullet dA }[/math]

For r1<R, we know the line integral of dA is just the circumference of the gaussian surface we took, a sphere of radius r1.

[math]\displaystyle{ \frac{Q}{\varepsilon_0} = E\bullet 4\pi r_1^2 }[/math]

Since we're taking a portion of the sphere we need to find the portion of the charge that is inside of the Gaussian surface. This is as easy as a ratio of volumes.

[math]\displaystyle{ q = \frac{3Q}{4\pi r_1^3}*\frac{4\pi R^3}{3} }[/math]

[math]\displaystyle{ q = Q\frac{r_1^3}{R^3} }[/math]

[math]\displaystyle{ E = Q\frac{r_1}{4\pi R^3} }[/math]

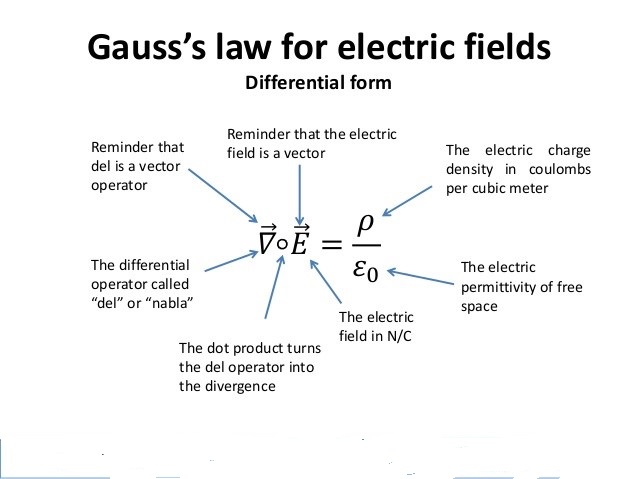
Differential Form

Unless charges are motionless or moving very slowly compared to the speed of light, there is a flaw in an attempt to calculate electric field at some location by using coulomb's law. The problem is relativistic retardation. The electric field depends on where fast moving particles were at some time in the past, not where they are now. Therefore, Coulomb's law is not consistent with the theory of special relativity. Gauss's law is consistent with relativity.

Divergence

The property of electric field called the"divergence" can relate the charges at the same location and time.

If there is a positive charge inside a small volume, the electric field directions "diverge", the net electric flux is positive, and div(E) is positive. If there is negative charge inside the tiny volume, the electric field directions converge ("antidiverge"), the net electric flux i negative, and div(E) is negative.

Divergence is Relativistically Correct

This is called a local relationship between charge and field, because the charge and the divergence property are evaluated at the same location and time, rather than at different locations and times. This avoids the problems of relativistic retardation and forma=s the basis for what is called a local field theory that is consistent with special relativity

Connectedness

Most of the applications of Gauss's Law are finding the electrical fields of different shapes. It can be observed that using Gauss's Law can assist in finding the derivation of the electric field for objects such as a sphere, sheet of charge, and cylinder. This use of Gauss's Law is especially useful in the field of Physics due to its aid in simplifying the calculations (as opposed to using Coulomb's Law) in finding the total charge inside a closed surface. Furthermore, the use of electric flux in Gauss's Flux Theorem assists in studying and understanding Faraday's Law and its applications to objects such as electrical generators, transformers, and inductors.

History

Gauss's Law was formulated by Fredreich Gauss in 1835 as a different way to derive Coulomb's Law, and remains as one of Maxwell's equations, the four equations that make up classical electrodynamics.