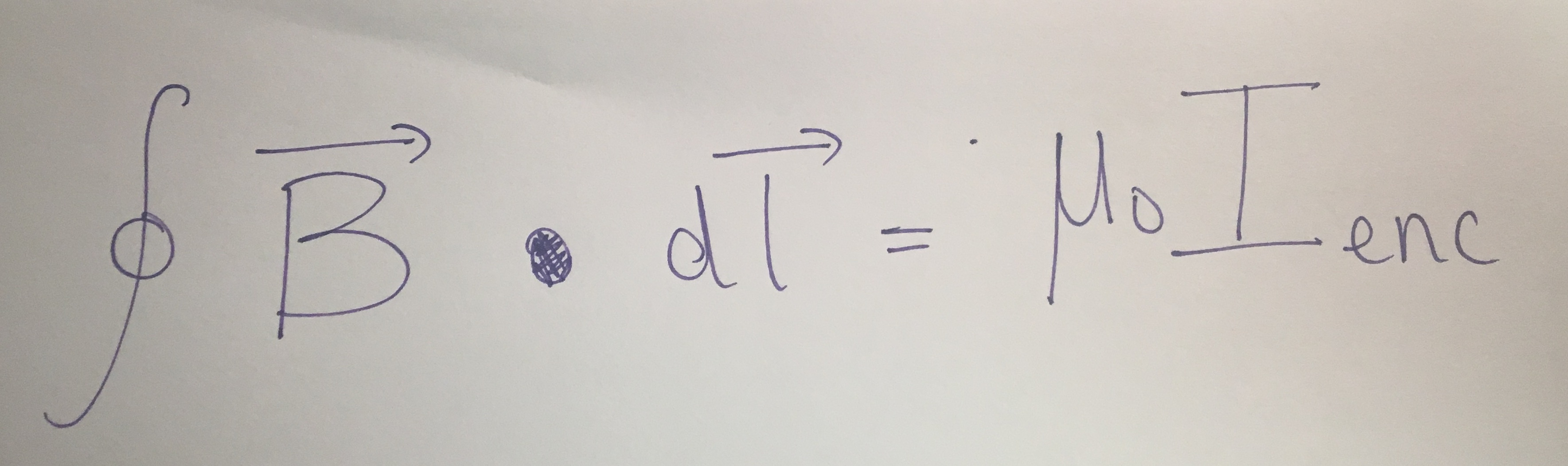Magnetic Field of a Long Thick Wire Using Ampere's Law
Claimed by Oluwasanmi Toyobo (Spring 2017)
The Main Idea
This page will explain and show how to use Ampere's Law to find the magnetic field of a long thick wire. It is much easier to calculate the magnetic field using Ampere's Law as opposed to Biot-Savart Law.
Mathematical Model for Ampere's Law
Ampere's Law is a quantitative relationship between the pattern of the magnetic field along a closed path and the amount of constant current passing through that path. It's important to remember that the equation for Ampere's Law applies to any kind of loop that has a constant current flowing through it. Ampere's Law is shown below:
We will see how one can use Ampere's Law to calculate the magnetic field of a long thick wire in examples below.
Examples
Simple
What is the magnetic field at a point 0.03 m away from a wire that has a current of 7 amperes?
Solution: [math]\displaystyle{ I=7 }[/math] and [math]\displaystyle{ r=0.03 }[/math]. So inserting this into the formula gives [math]\displaystyle{ {B = \frac{μ_0(7)}{2π(0.03)}} }[/math]. This results in 4.67e-5 T
Middling
A long straight wire suspended in the air carries a conventional current of 7.4 amperes in the -x direction as shown (the wire runs along the x-axis). At a particular instant an electron at location < 0, -0.004, 0 > m has velocity < -3.5 e5, -4.2 e5, 0 > m/s. What is the magnetic field due to the wire at the location of the electron?
Solution: [math]\displaystyle{ {B = \frac{μ_0(7.4)}{2π(0.004)}} }[/math] and use right hand rule. The answer is < 0, 0, 3.7e-4 > T.
Hard
Using the same values as in the middling problem calculate the magnetic force on the electron due to the wire.
Solution: The formula for magnetic force is [math]\displaystyle{ qv×B }[/math]. So by using the value for B computed above and calculating the cross product between B and qv we find that this equals < 2.49e-17, -2.07e-17, 0 > N. Don't forget that because this is the force on an electron q is negative.
History
In 1826, it was Hans Christian Oersted who had discovered the connection between magnetism and electricity when he found that the needle of a compass he was holding was deflected when he moved it close to a current carrying wire during one of his lectures. It was this discovery that prompted Andre-Marie Ampere to start his own research. Ampere was conducting experiments to learn more about the magnetic fields created by currents. Ampere found that when he placed two wires next to each other with current running in the same direction, the wires were attracted to each other and when the current was running in opposite directions, the wires repelled each other! Experiments like this and more gave way to the creation of Ampere's Law that helps people calculate the strength of magnetic fields and currents in particular situations.
See also
See the page on Ampere's Law for a more in depth look at the law itself: Ampere's Law
For more applications of Ampere's Law see: Magnetic Field of a Toroid Using Ampere's Law and Magnetic Field of Coaxial Cable Using Ampere's Law
Further reading
Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley.
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html
https://en.wikibooks.org/wiki/Electrodynamics/Ampere%27s_Law
References
Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley. page 887.