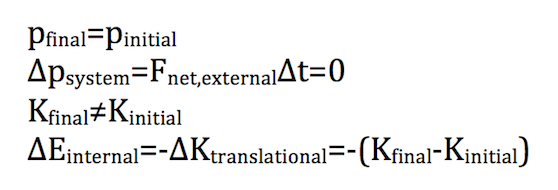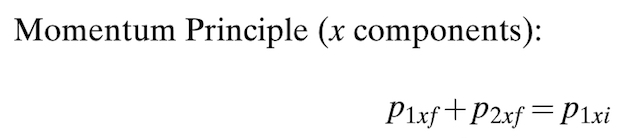Inelastic Collisions

Created by Csorensen6

Edited/Claimed by Vansh Kareer, Spring 2017

This topic covers the concept of inelastic collisions and the results of the collisions on the bodies involved. Included are the methods that can be applied to solve problems related to these types of collisions, along with worked examples.

General Concept

Inelastic collisions are collisions during which the momentum of the interacting bodies is conserved, but the kinetic energy is not. This change in kinetic energy from initial to final states is what differentiates inelastic collisions from elastic collisions. Generally, the forces involved in an inelastic collisions are so large relative to external forces that those external forces can be ignored. Consequently, given that ΔPsystem = Fnet,ext*ΔT, if we approximate Fnet,ext as zero, then ΔPsystem = 0, and Pi = Pf.

Because the final kinetic energy differs from the initial kinetic energy, inelastic collisions witness a change in the internal energy of the objects involved in the collision. A change in internal energy often manifests itself in the form of deformation, rotation, heat, vibration, explosions, or energy state excitation. In these collisions, the change in internal energy is equal to the negative change in kinetic energy. Based on these characteristics, and applying the momentum principle, a few basic equations can be set to outline an inelastic collision.

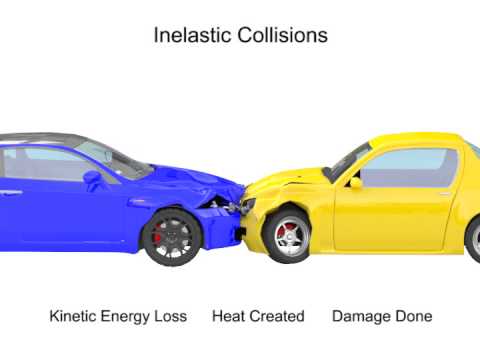
The picture below illustrates some characteristics of a typical, inelastic collision: a car crash.

In the car crash depicted above, there is a loss of kinetic energy, which is converted into internal energy in the form of produced heat and metal deformation of the two colliding cars. This is in accordance with the relation ΔEinternal = -ΔKtrans=-0.5*mass*(Δvelocity)^2.

Types of Inelastic Collisions

Maximally Inelastic Collisions

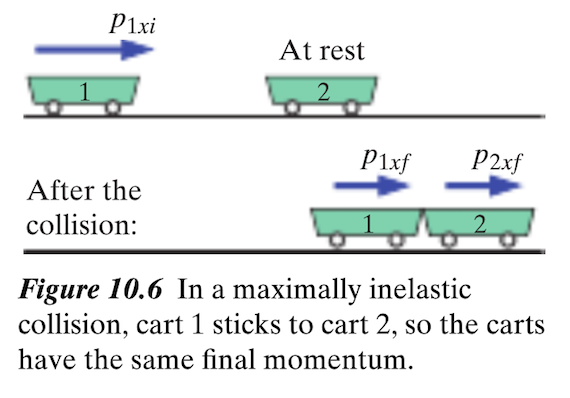
One of the most commonly-seen situations is the maximally inelastic collision, also known as the perfectly inelastic collision, in which two objects collide and then remain connected for the duration of the observable interaction. This does not indicate an end to movement, as momentum must be conserved by the end of the interaction. See problem 1 for an example. More information about such problems can be found in the page about maximally inelastic collisions.

Explosions

In these types of problems, an object bursts apart, and some of its internal energy is converted into kinetic energy. As a result, ΔK is actually positive and ΔEint is actually negative, in that internal energy is used up in the course of the explosion and causes an increase in the speed of the particles involved. This can be seen in the relation Ki < Kf, wherein the change in internal energy of the lends itself to the increase in kinetic energy from Ki to Kf, which directly correlates to an increase in particle speed in the explosion's aftermath.

Typical Inelastic Collisions

In these types, two or more objects collide but do not stick together, but as a result of their collision, one or both begin to rotate, vibrate, deform, heat up, etc. In these problems, there is a positive ΔEint and a negative ΔK, and Ki > Kf. Most real-world collisions are typically inelastic, albeit to varying degrees. An example of a typically inelastic collision is a car crash.

Typical Process for Solving

In such problems, it is often necessary to apply both the momentum principle and the energy principle.

The steps for solving inelastic collision problems are often as follows:

1) Draw a picture of the initial and final states.

2) Given that collisions involve extremely large forces acting over short time intervals, it is accurate to say that Fnet,ext = 0, because the external forces are typically much, much smaller than the internal forces involved in the collision.

3) Knowing that Fnet,ext = 0, this means that momentum is conserved and that Pf = Pi. This comes from the momentum principle, in that ΔPsystem = Fnet,ext*ΔT, and if Fnet,ext is zero, then the right side of that equation is also zero.

4) Next, knowing that Pf = Pi, you can solve for any unknown velocities of the objects involved via the momentum principle.

5) Having determined the velocity of each object, you can then determine the initial and final kinetic energies of the system using K = (1/2)*m*|v|^2 for each object.

6) Next, you can find the change in kinetic energy, or ΔK, and this will be equal to the negative change in the internal energy (whether it be heat, rotation, etc.) gained by the objects in the course of the collision. In other words ΔEint = -ΔK.

Examples

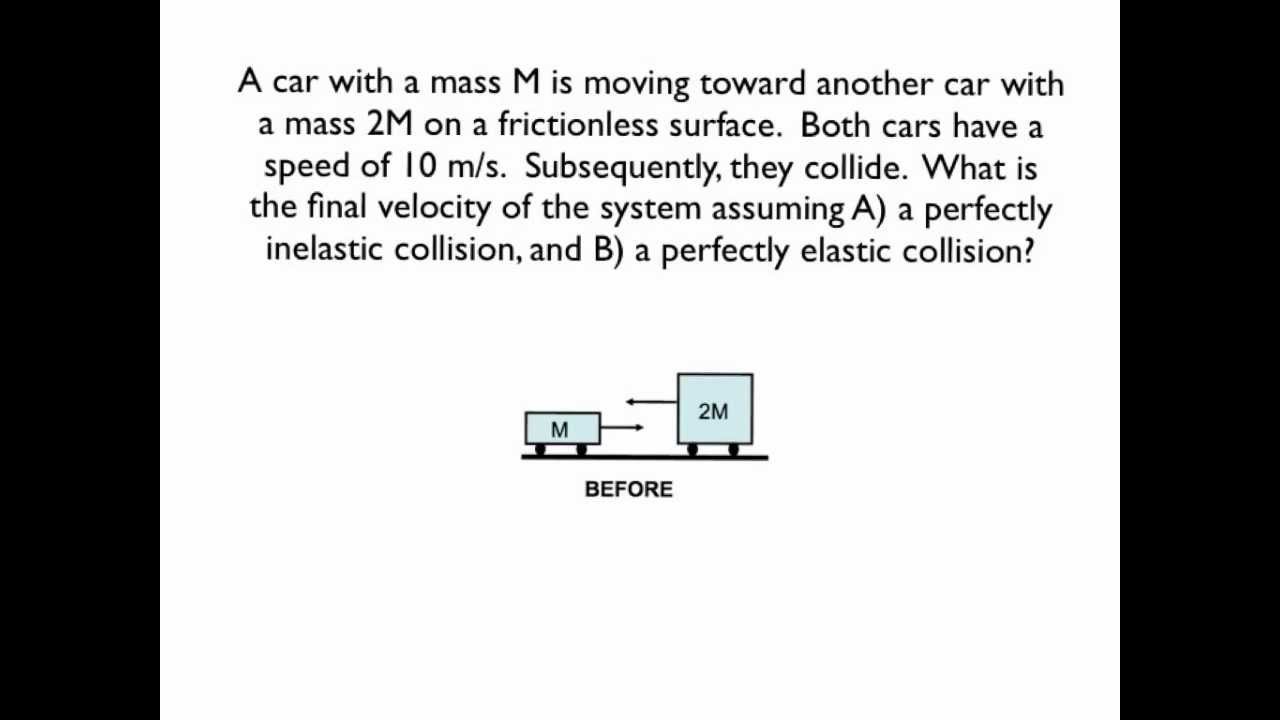
Simple

Just do part A.

a)

  ΔP = Pf - Pi = Fnet,ext*ΔT = 0       
  Pi = Pf

  2M <-10,0,0> + M<10,0,0> = (2M + M)*vf
  <-10M,0,0> = 3M * vf

  vf = <-3.33, 0, 0> m/s

Middling

There are two hockey pucks traveling across the surface of a frozen pond. The first puck has a mass of 0.15 kg and is moving with a velocity of <2.5, 3.4, 0> m/s. The second puck has a mass of 0.13 kg and is moving with a velocity of <-3.1, 1.7, 0> m/s. After colliding, the first puck then has a velocity of <-1.9, 3.0, 0> m/s. (Reference the image below).

a) What is the velocity of the second puck after the collision?

b) What is the initial kinetic energy?

c) What is the final kinetic energy?

d) What is the change of the internal energy of the two pucks?

Answer

a)

  ΔP = Pf - Pi = Fnet,ext*ΔT = 0       
  Pi = Pf

  0.15kg<2.5, 3.4, 0> m/s + 0.13kg<-3.1, 1.7, 0> m/s = 0.15kg<-1.9, 3.0, 0> m/s + 0.13kg*v
  <-0.028, 0.731, 0> kg*m/s = <-0.285, 0.45, 0> kg*m/s + 0.13kg*v
  <0.257,0.281,0> kg*m/s = 0.13kg*v

  v = <1.977, 2.162, 0> m/s

b)

  K = (1/2)*m*|v|^2     
  |v| = (vx^2 + vy^2 + vz^2)^(1/2)      
  |v|^2 = vx^2 + vy^2 + vz^2
     
  Ki = (1/2)*0.15kg*((2.5 m/s)^2 + (3.4 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((-3.1 m/s)^2 + (1.7 m/s)^2 + (0 m/s)^2)
  Ki = 1.336 J + 0.813 J

  Ki = 2.149 J

c)

  K = (1/2)*m*|v|^2     
  |v| = (vx^2 + vy^2 + vz^2)^(1/2)      
  |v|^2 = vx^2 + vy^2 + vz^2

  Kf = (1/2)*0.15kg*((-1.9 m/s)^2 + (3.0 m/s)^2 + (0 m/s)^2) + (1/2)*0.13kg*((1.977 m/s)^2 + (2.162 m/s)^2 + (0 m/s)^2)
  Kf = 0.946 J + 0.558 J

  Kf = 1.504 J

d)

  ΔE = Q + W = ΔK + ΔEinternal + ΔU + ΔErest
  ΔE = ΔK + ΔEinternal = 0 = Kf - Ki + ΔEinternal

  1.504 J - 2.149 J + ΔEinternal = 0
  -0.645J + ΔEinternal = 0

  ΔEinternal = 0.645 J

Difficult

A lit firework of mass 15 kg is launched into the sky with an initial velocity of <10,17,0> m/s. Eventually, its fuse burns up and the firework explodes, bursting into four parts. One piece has a mass of 3 kg and a velocity of <8,7,0> m/s. Another has a mass of 4 kg and a velocity of <15,0,0> m/s. The third has a mass of 3.5 kg and a velocity of <12,-5,0> m/s.

Reference the picture below.

a) What is the mass of the fourth piece?

b) What is the momentum and velocity of that piece?

c) What is the change in internal energy?

d) Justify the sign of the answer found in part c).

Answer

a)

  m1 = m2 + m3 + m4 + m5
  15 kg = 3 kg + 4 kg + 3.5 kg + m5
  15 kg = 10.5 kg + m5
  
  m5 = 4.5 kg

b)

  ΔP = Pf - Pi = Fnet,ext*ΔT = 0       
  Pi = Pf
  
  15 kg <10,17,0> m/s = 3 kg <8,7,0> m/s + 4 kg <15,0,0> m/s + 3.5 kg <12,-5,0> m/s + p5
  <150,255,0> kg*m/s = <24,21,0> kg*m/s + <60,0,0> kg*m/s + <42,-17.5,0> kg*m/s + p5
  <150,225,0> kg*m/s = <126,3.5,0> kg*m/s + p5
  
  p5 = <24,251.5,0> kg*m/s

  p = mv
  p5 = m5v5
  <24,251.5,0> kg*m/s = 4.5kg*v5
  
  v5 = <5.33,55.89,0> m/s

c)

  ΔE = Q + W = ΔK + ΔEinternal + ΔU + ΔErest = 0
  ΔE = ΔK + ΔEinternal = 0 = Kf - Ki + ΔEinternal
  ΔEinternal = Ki - Kf

  ΔEinternal = (1/2)(15)(10^2 + 17^2 + 0^2) - (1/2)(3)(8^2 + 7^2 + 0^2) - (1/2)(4)(15^2 + 0^2 + 0^2) - (1/2)(3.5)(12^2 + (-5)^ + 0^2) - (1/2)(4.5)(5.33^2 + 55.89^2 + 0^2)
  ΔEinternal = 2971.5 - 169.5 - 450 - 295.75 - 7092
 
  ΔEinternal = -5036 J

d)

  The final kinetic energy is greater than the initial kinetic energy, and this is because, by exploding, some of the internal energy stored in the firework was released and then harnessed as kinetic energy. 
  Consequently, the change in internal energy is negative.

Connectedness

The science of collisions and the study of momentum are especially prominent when it comes to the sport of football, and particularly in regards to concussions, or traumatic brain injuries sustained due to hard blows to the head. Significant research within the biomedical field is being conducted into how to reduce concussion frequency and severity, and this often entails specifically designing helmets to minimize the impact of high-speed, hard-hitting tackles. This research has come to greater prominence with the relatively-recent discovery of the role football plays in the acquisition of CTE, a degenerative disease which slowly causes the loss of cognitive function, similar to dementia, and which is especially prominent among football players and other athletes who suffer repeated head trauma.

References

Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print