Momentum Principle
This page discusses the Momentum Principle and examples of how it is used.
Claimed by Brandon Kang for Spring 2017
Claimed by hyk96610
Claimed by dansher3 (Daniel Ansher) for Fall 2016
The Main Idea
The Momentum Principle is the first fundamental principle of mechanics and describes the relationship between the change in momentum of a system and the total amount of interaction (or total amount of force) within the surroundings. In terms of the system and surroundings, both can be set in any way necessary, where the system may just include a person or the entire Earth. The Momentum Principle can be used in nearly all situations, and it is typically advised to start a problem by first writing out the Momentum Principle and then branching out (by rearranging or substituting values) in order to solve a problem. Overall, the momentum principle assumes that the final momentum is dependent on the initial momentum, the force applied, and the duration in which the force is applied.
Momentum, in general, is a property and by nature is consisted of velocity and mass and is consequently directly proportional to the magnitude of the mass and velocity of any particular object. This in turn determines the required amount of force and time required to stop it. This section focuses on linear momentum as opposed to angular momentum (which is when an object is rotational in motion).
A Mathematical Model
The Momentum Principle is defined as [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system}= \vec{F}_{net} }[/math] (or [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]). As a result, the momentum principle can alternatively be written as [math]\displaystyle{ \vec{p}_{f}=\vec{p}_{i}+\vec{F}_{net}* {∆t} }[/math].
[math]\displaystyle{ \vec{p} }[/math] is the momentum of the system. In the equation, momentum (measured in [math]\displaystyle{ kg*{\frac{m}{s}} }[/math] ) is expressed as the "change in momentum" ([math]\displaystyle{ ∆\vec{p} = \vec{p}_{final} - \vec{p}_{initial} }[/math]), which includes both the magnitude and direction of the momentum. Therefore, momentum is a vector quantity.
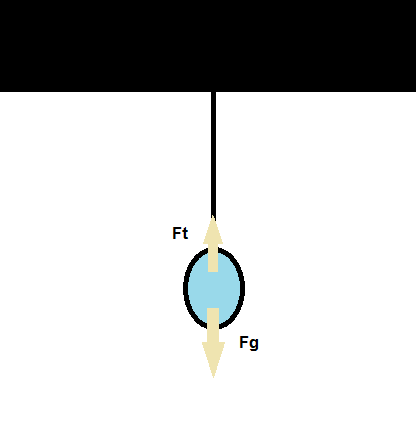
[math]\displaystyle{ \vec{F}_{net} }[/math] is the net force from the surroundings. Force (measured in Newtons, or N) includes the interactions between system and the surroundings, like the gravitational force exerted by the Earth on us or the force that a compressed spring exerts on a mass. Because momentum is defined as a vector, in the Momentum Principle, the force includes both the magnitude and direction. Also, it is important to note that the Momentum Principle calls for the net force, which is the sum of all the different forces from the surroundings, like adding both the force of gravity and the force of the spring together to calculate the net force. Because of this, it is even more crucial to pay attention to the direction of the forces as a positive or negative sign error could cause an error in the calculated net force. Therefore, a free body diagram of the system and the forces acting on the system is a helpful way to determine the various forces acting on the system. For example, a free body diagram of a very simplistic model of a ball held by a string is demonstrated below in order to analyze the forces acting on the ball.
Therefore, in the above example, the net force acting on the ball is 0. We can conclude this through the momentum principle such that initial and final momentum are equal due to the ball not moving. Therefore, [math]\displaystyle{ ∆\vec{p}=0 }[/math], and thus [math]\displaystyle{ \vec{F}_{net} = 0 }[/math]. Because the net force is equal to zero, this means that the force due to tension is equal in magnitude and opposite in direction to the force due to gravity.
[math]\displaystyle{ t }[/math] is the time (measured in seconds, or s). Specifically, the Momentum Principle calls for the "change in time" ([math]\displaystyle{ ∆\vec{t} = \vec{t}_{final} - \vec{t}_{initial} }[/math]), or in other words, the duration of the interaction is needed. Overall, if a force is applied to a system over a greater duration, the change in momentum is greater, as the momentum principle, [math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math], also demonstrates that the change in momentum is directly proportional to the duration of the applied force.
The Momentum Principle can be further manipulated to find the change in velocity of the system. This is represented by the formula: [math]\displaystyle{ \vec{v}_{f}=\vec{v}_{i}+{\frac{\vec{F}_{net}}{m}}*{∆t} }[/math].
[math]\displaystyle{ \vec{v}_{f} }[/math] is the final velocity of the system, and [math]\displaystyle{ \vec{v}_{i} }[/math] is the initial velocity of the system. The difference between the two can be shortened to [math]\displaystyle{ \vec{{∆v}} }[/math], and represents the change in velocity of the system.
[math]\displaystyle{ \vec{F}_{net} }[/math] is the net force acting on the system.
[math]\displaystyle{ m }[/math] is the mass of the system.
[math]\displaystyle{ {∆t} }[/math] is the change in time of the system in which it is acted on by the force.
This manipulation of the momentum principle is very useful when it comes to updating the position of the system because it gives you the change in velocity over the observed time interval.
A Computational Model
Click on the link to see the Momentum Principle through VPython!
Make sure to press "Run" to see the principle in action!
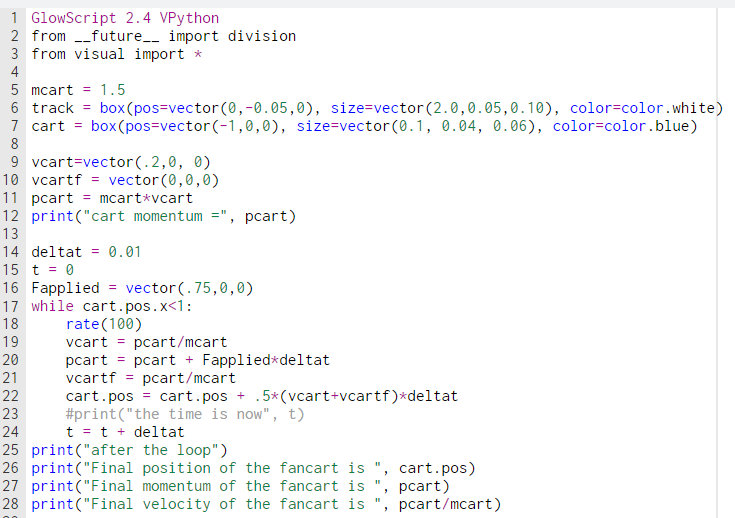
Below is another demonstration of the Momentum Principle that involves a fan cart traveling on a track with an applied force.
Breaking Down the Code
In the next example, we will analyze the code to observe how the fan cart moves and gains momentum.
In lines 5-10, we initialize the values of the mass, velocity, and momentum of the fan cart, which is crucial and necessary for the code to not error when it enters the iteration, as these values must be defined. Line 14 defines the [math]\displaystyle{ {∆t} }[/math], which should be a small value to avoid inaccurate measurements of the final position, momentum, and velocity. Allowing [math]\displaystyle{ {∆t} }[/math] to be a large number would lead to inaccurate estimations of the change in momentum, and the momentum principle utilizes the derivative of momentum with respect to time, thus smaller measurements of [math]\displaystyle{ {∆t} }[/math] should be used. Lines 15-16 initialize the values of the constant, applied force. Although this force is constant, it will increase the momentum of the fan cart through each iteration since the force applied is in the same direction as the momentum.
Entering the iteration, the momentum of the cart is updated with the Momentum Principle. We must keep track of initial and final values of velocity before and after the Momentum Principle is utilized, as we use the average velocity defined as the numerical average of the initial and final values of velocity due to a constant force acting on the system. Therefore, the final velocity is updated after the Momentum update. The iteration continues until the cart has reached the end of the track, which is defined only on the x axis, and the final values of the momentum, position, and velocity are printed.
Examples
Simple
Two external forces <40,-70,0>N and <20,10,0>N, act on a system. What is the net force acting on the system?
Answer: <60,-60,0>N
Explanation:
The net force is just synonymous for the overall force acting on the system. In this case, this is the sum of the forces given in the problem above.
[math]\displaystyle{ \vec{F}_{net} = \vec{F}_{1} + \vec{F}_{2} }[/math]
[math]\displaystyle{ \vec{F}_{net} }[/math] = <40,-70,0)N + <20,10,0>N = <60,-60,0>N
Middling
A hockey puck is sliding along the ice with nearly constant momentum <10,0,5>kg*m/s when it is suddenly struck by a hockey stick with a force <0,0,2000>N that lasts for only 3 milliseconds (3e-3s). What is the new (vector) momentum of the puck?
Answer: <10,0,11>kg*m/s
Explanation:
In this example, we are manipulating the momentum principle in order to calculate the new momentum at a given time. This is also called the update momentum formula.
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} - \vec{p}_{initial} }[/math] = [math]\displaystyle{ \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} }[/math] - <10,0,5>kg*m/s = <0,0,2000>N * (3e-3)s
[math]\displaystyle{ \vec{p}_{final} }[/math] = <10,0,11>kg*m/s
Difficult
In outer space a rock of mass 5kg is acted on by a constant net force <29,-15,40>N during a 4s time interval. At the end of this time interval the rock has a velocity of <114,94,112>m/s. What is the rock's velocity at the beginning of the time interval?
Answer: <90.8,106,80>m/s
Explanation:
This example is similar to the first example. Only now, instead of manipulating variables to solve for momentum, we must manipulate the variables to solve for velocity, specifically initial velocity. Velocity can be connected to the momentum principle since momentum is just mass multiplied by velocity.
[math]\displaystyle{ ∆\vec{p} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p}_{final} - \vec{p}_{initial} = \vec{F}_{net} * {∆t} }[/math]
[math]\displaystyle{ \vec{p} = m * \vec{v} }[/math]
[math]\displaystyle{ m\vec{v}_{final} - m\vec{v}_{initial} = \vec{F}_{net} * {∆t} }[/math]
(5kg * <114,94,112>m/s) - (5kg * [math]\displaystyle{ \vec{v}_{initial} }[/math]) = <29,-15,40>N * 4s
[math]\displaystyle{ \vec{v}_{initial} }[/math] = <90.8,106,80>m/s
Connectedness
Why the Momentum Principle Connects to Your Interests
All over the world and at every point in time, interactions are continuously occurring, and I thought it was interesting to see how the Momentum Principle was the most fundamental principle that is used in starting to the analyze the different interactions. This fundamental idea allows us to examine how items collide, interact with each other, and most importantly, allow us to gain knowledge about how our everyday lives work as a whole.
How the Momentum Principle Connects to Your Major
Computer Science
While the momentum principle is often related to the tangible physical world, there are applications or tools when building software applications that apply to computer science. For example, if I was a software engineer trying to create Roller Coaster Tycoon, I would need to virtually calculate the correct and verifiable momentums for the roller coasters to mimic real world movements. This idea can even be expanded with relation to robotics where computer scientists aim to make hardware movement mimic human movement in the real world. Again, while not directly related, the concept of momentum and this fundamental idea must be learned and incorporated in order to benefit the future of technologies, especially with regard to the computer science realm.
Interesting Industrial Applications
While the Momentum Principle is not directly connected to the applications, it is often used in the process (especially in the beginning) of industrial application. For example, when creating life saving airbags and seat belts for cars, the Momentum Principle is used. The final momentum of a car during an accident would be zero, or would stop, and the initial momentum would be based on the mass and velocity of the car. With the change in momentum fixed, the airbag and seat belt would focus on increasing the time taken for the body's momentum to reach zero (final momentum), which would consequently reduce the force of the collision and protect the body from getting as injured. With the Momentum Principle being applicable in so many areas of my life, I found the concept even more interesting.
History
Although the Momentum Principle is credited as Newton’s second law of motion, it is difficult to just credit Isaac Newton (1643AD – 1727AD) for the development of the principle. As the Momentum Principle is the quantitative and more in-depth representation of Newton’s first law of motion (“An object tends to be at rest or moves in a straight line and a constant speed except to the extent that it interact with other objects”), the development of the first law also serves an important role in the history of the Momentum Principle. Aristotle (384BC – 322BC) initially proposed that objects had the natural tendency to be at rest and that a push (or a force) was absolutely needed to keep the object moving. His proposal was challenged by Galileo (1564AD – 1642AD), who introduced the idea that objects had the natural tendency to travel in a straight line at constant speed unless something (or a force) was interacting with something. Likewise, Descartes (1596AD – 1650AD) also contributed as he proposed three laws of nature in his “Principle of Philosophy,” which actually outlined the later published Newton’s first law of motion. After studying Descartes, Newton adopted Descartes’ principles as his first law of motion, and alongside the famous story of Newton sitting under an apple, Newton was able to create the Momentum Principle, or his second law of motion.
Why is this principle so important to us?
While we have known about the momentum principle for quite a long time now, many (including students) still wonder why the momentum principle is so important and crucial to learn. The reality of the matter is that this fundamental principle applies to many real world applications and can explain movement in the world of science. Whether its examining collisions between objects or impact breaking/building, the principle is a practical and useful way for us to explain how our real physical world works.
See also
As the Momentum Principle is the first of three fundamental principles of mechanics, the next possible topics to examine would be the other fundamental principles, the Energy Principle and the Angular Momentum Principle. Also, although the Momentum Principle is an extremely important concept that usually signals the start of a momentum related problem, the principle branches out into other momentum topics like Impulse and Iterative Prediction, which are used to solve other types of problems.
Further Reading
[1] http://espace.library.uq.edu.au/view/UQ:273253/Pap_290f_postprint.pdf
[2] http://authors.library.caltech.edu/2577/1/TOLpr30c.pdf
External links
[2] https://www.youtube.com/watch?v=ZvPrn3aBQG8
References
[1] Harris, William. "How Netwon's Laws of Motion Works." HowStuffWorks. HowStuffWorks.com, 29 July 2008. Web. 29 Nov. 2015. <http://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion.htm>
[2] Sherwood, Bruce A. "2.1 The Momentum Principle." Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics.
[3] Fenton, Flavio. "Momentum and Second Newton's Law." 26 Aug. 2015. Lecture.