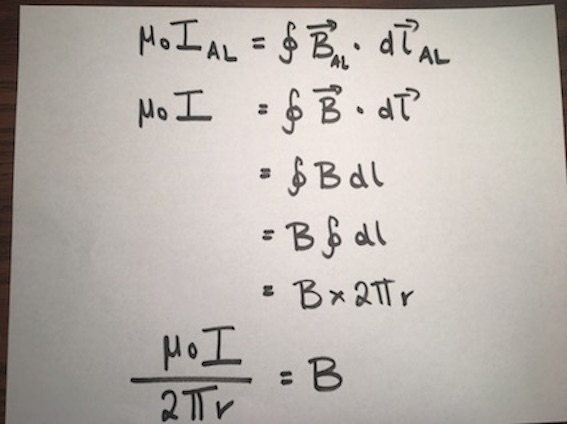Magnetic Field of a Long Thick Wire Using Ampere's Law
Claimed by Oluwasanmi Toyobo (Spring 2017)
The Main Idea
This page will explain and show how to use Ampere's Law to find the magnetic field of a long thick wire at a specified distance. It is much easier to calculate the magnetic field using Ampere's Law as opposed to Biot-Savart Law.
Mathematical Model for Ampere's Law
Ampere's Law is a quantitative relationship between the pattern of the magnetic field along an Amperian loop and the amount of constant current passing through that path. An Amperian loop is essentially a closed loop that can be any size. On this page, the Amperian loop will be circular. Also, It's important to remember that the equation for Ampere's Law only applies to an Amperian loop that has a constant current flowing through it. Ampere's Law is shown below:
The following pictures display how to use Ampere's Law when trying to calculate the magnetic field of a current flowing out of the page at distance r away from the wire.
The diagram above shows a current-carrying wire with its current flowing out of the page. Using the right-hand rule, we can determine the direction of the magnetic field to be as shown. The dotted circle represents the Amperian loop of radius r.
The workings below, shows how Ampere's Law is used to calculate the magnetic field of the current-carrying wire at a distance r. Note that on the third line of working, the dot product disappears. This occurs because the direction of the magnetic field is the same as the direction of dl. More specifically, the angle between dl and the magnetic field B is 0. Remember the equation of the dot product is |a| x |b| x cos (theta). So in this case, a = B, b = dl and theta = 0. So if theta = 0 we know that cos (0) = 1. In the next line of working B is pulled out of the closed integral, this occurs because all along the Amperian loop the magnetic field is the same, it does not change in magnitude. In the next line of working, once we added up all the dl 's on the Amperian loop, that will give us the circumference of the Amperian loop. From there we make B the subject of the equation.
We will see how one can use Ampere's Law to calculate the magnetic field of a long thick wire in examples below.
Examples
Simple
A long thick wire has radius r = 0.1 m and a constant current of I = 0.15 A. The Amperian loop within the wire has radius r = 0.03 m. Calculate the magnetic field through the Amperian loop.
Explanation of the solution:
- 1) Write out Ampere's Law. The enc written as a subscript of I is short for enclosed.
- 2) For the current, you only want the current that is enclosed within the loop of radius r, not all of the current enclosed within the loop of radius R. To calculate the desired current, multiply the given current I by a ratio of the Amperian loop's area over the area of long thick wire.
- 3) Substitute the desired current into the equation.
- 4) Remove the dot product on the right hand side of the equation because the direction of the magnetic field on the Amperian loop is the same as the direction of dl
- 5) Pull B out of the closed integral because it is the same all along the Amperian loop.
- 6) Complete the integral to give you the circumference of the Amperian loop and make B the subject of the equation.
- 7) Substitute in the values to give you 9e-8 T
Middling
A long straight wire suspended in the air carries a conventional current of 7.4 amperes in the -x direction as shown (the wire runs along the x-axis). At a particular instant an electron at location < 0, -0.004, 0 > m has velocity < -3.5 e5, -4.2 e5, 0 > m/s. What is the magnetic field due to the wire at the location of the electron?
Solution: [math]\displaystyle{ {B = \frac{μ_0(7.4)}{2π(0.004)}} }[/math] and use right hand rule. The answer is < 0, 0, 3.7e-4 > T.
Hard
Using the same values as in the middling problem calculate the magnetic force on the electron due to the wire.
Solution: The formula for magnetic force is [math]\displaystyle{ qv×B }[/math]. So by using the value for B computed above and calculating the cross product between B and qv we find that this equals < 2.49e-17, -2.07e-17, 0 > N. Don't forget that because this is the force on an electron q is negative.
History
In 1826, it was Hans Christian Oersted who had discovered the connection between magnetism and electricity when he found that the needle of a compass he was holding was deflected when he moved it close to a current carrying wire during one of his lectures. It was this discovery that prompted Andre-Marie Ampere to start his own research. Ampere was conducting experiments to learn more about the magnetic fields created by currents. Ampere found that when he placed two wires next to each other with current running in the same direction, the wires were attracted to each other and when the current was running in opposite directions, the wires repelled each other! Experiments like this and more gave way to the creation of Ampere's Law that helps people calculate the strength of magnetic fields and currents in particular situations.
See also
See the page on Ampere's Law for a more in depth look at the law itself: Ampere's Law
For more applications of Ampere's Law see: Magnetic Field of a Toroid Using Ampere's Law and Magnetic Field of Coaxial Cable Using Ampere's Law
Further reading
Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley.
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html
https://en.wikibooks.org/wiki/Electrodynamics/Ampere%27s_Law
References
Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley. page 887.