Vectors
Written by Elizabeth Robelo
Improved by Aparajita Satapathy
Improved by Lichao Tang
Improved by Jimin Yoon
Improved by Sabrina Seibel
Claimed: Sanjana Kumar Fall 2017
Improved by Audrey Suh (Spring 2018)
In physics, a vector is a quantity with a magnitude and a direction.
The Main Idea
A vector is a quantity with a magnitude and a direction. The magnitude of a vector is a scalar quantity which represents the length of the vector but does not have a direction. A vector is represented by an arrow. The orientation of the vector represents its direction. The length of the vector represents its magnitude. When a vector is drawn, the starting point is the tail and the ending point is called the head, or the "tip", of the vector. In physics, a vector always starts at the source and directs to the observation location. In other words, if you are drawing a vector, the tail of the vector will be located at the original location, and the tip of the vector will be located at the observation location. Refer to the image below for a visual representation:

We can also add and subtract vectors. To add two vectors you align them head to tail and make sure that the tails of both vectors coincide with each other. The new added vector is the connecting arrow starting from the tail of one to the head of the other vector.
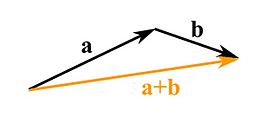
To subtract two vectors reverse the direction of the vector you want to subtract and continue to add them like shown before.
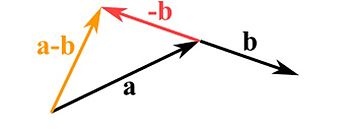
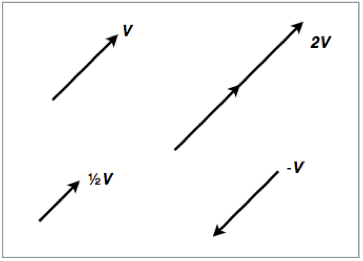
A vector can also be multiplied by a scalar. To multiply a vector by a scalar we can strech, compress or reverse the direction of a vector. If the scalar is between 0 and 1, the vector will be compresseed. If the scalar is greater than 1, the vector will get streched. If the scalar is a negative number, then the vector reverses its direction.
A Mathematical Model
Vectors are given by x, y, and z coordinates. They are written in the form <x, y, z> or (xi + yj - zk). Magnitude: [math]\displaystyle{ |A| = \sqrt{x^2 + y^2 + z^2} }[/math]
Dot Product: Ia·bI = IaI*IbI*cos([math]\displaystyle{ theta }[/math])
[math]\displaystyle{ \mathbf{A}\cdot\mathbf{B}=\sum_{i=1}^n A_iB_i=A_1B_1+A_2B_2+\cdots+A_nB_n }[/math]
Addition of two vectors: <a1, a2, a3> + <b1, b2, b3> = <a1 + b1, a2 + b2, a3 + b3>
Unit Vector: :[math]\displaystyle{ \mathbf{\hat{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|} }[/math]
Cross Product: Ia x bI =IaI*IbI*sin([math]\displaystyle{ theta }[/math])
a x b= <a1, a2, a3> x <b1, b2, b3> = <a2*b3 - a3*b2> i - <a1*b3 - a3*b1> j + <a1*b2 - a2*b1> k
Multiplication between vectors and scalars: c<a1, a2, a3> = <c*a1, c*a2, c*a3>
A Computational Model
VIDLE is an interactive editor for VPython. It is commonly used in Physics to visualize 3D motion and preform repetitive calculations from fundamental principles. Codes on VIDLE contain a sequence of instructions for a computer to follow. File:Vectorcode.jpeg In VIDLE code, arrow objects usually represent vector components. Arrows contain 3 parts: pos, axis, and color. Each part can be manipulated to achieve different results. The pos and axis of arrows are vectors, so you can multiply them by scalar quantities to scale them. Arrows are often used to represent relative position vectors, starting at position A and ending at position B. This is found the commonly use phrase "final minus initial" (B-A). In the above code, the relative position vector is of the tennis ball with respect to the baseball, so the arrow points from the baseball to the tennis ball. 3 arrows (vectors) can be used as components on a coordinate system for a vector. They can represent the position vector in each coordinate direction. You can reference the z component vector using the formula vectorname.z. same goes for y and z.
In Physics 2, you need to know that a vector always starts at a source and points to an observation location you want to get physical quantities(such as electric field, magnetic field, etc.) at. Also, you should be able to calculate the magnitude and direction of the vector in 3D space. Here is an example of a VPython model that computationally calculates such values. (The green arrow represents the position vector that starts from the source, which is a proton(red ball), to the arbitrary observation location.) (Click Run on the upper left corner in order to display the model.)
3D Vector
Examples
Simple
Which of the following statements is correct? (Can be more than one)
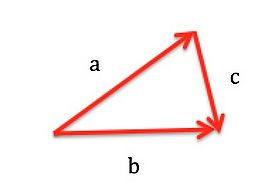
1. [math]\displaystyle{ \overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} }[/math]
2. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{b} - \overrightarrow{c} }[/math]
3. [math]\displaystyle{ \overrightarrow{a} = \overrightarrow{c} + \overrightarrow{b} }[/math]
4. [math]\displaystyle{ \overrightarrow{b} = \overrightarrow{c} + \overrightarrow{a} }[/math]
The answer is option number 2 and option number 4.
Middling
1. What is the magnitude of the vector C = A - B if A = <10, 5, 8> and B = <9, 4, 3>?
First we need to find the vector C: A - B = [math]\displaystyle{ \lt (10-9), (5-4), (8-3)\gt = \lt 1, 1, 5\gt = C }[/math]
[math]\displaystyle{ \sqrt{(1)^2 + 1^2 + 5^2} = 5.196 }[/math]
2. What is the cross product of A = <1,2,3> and B = <9,4,5>?
Use the equation for cross product: a x b= <a1, a2, a3> x <b1, b2, b3> = <a2*b3 - a3*b2> i - <a1*b3 - a3*b1> j + <a1*b2 - a2*b1> k
A x B[math]\displaystyle{ =\lt 2*5 - 3*4, 1*5 - 3*9, 1*4 - 2*9\gt = \lt -2, -22, -14\gt }[/math]
Difficult
What is the unit vector in the direction of the vector <10, 5, 8>? First you have to find the magnitude of the vector given: [math]\displaystyle{ \sqrt{10^2 + (5)^2 + 8^2} = 13.74 }[/math]
Finally divide the vector by its magnitude to get the unit vector:
[math]\displaystyle{ \tfrac{\lt 10, 5, 8\gt }{13.74} }[/math]
= <.727, .364, .582> Notice that the magnitude of the unit vector is equal to 1
Connectedness
1.Vectors will be used in many applications in most calculation based fields when movement and position are involved. Vectors can be two dimensional or three dimensional. Vectors are used to represent forces, fields, and momentum.
2.Vectors has been used in many application problems in engineering majors. In engineering applications, vectors are used to a lot of quantities which have both magnitude and direction. Dividing a magnitude into vector quantities in the x,y, and z directions clarify which components of a vector have quantity. For example, in Biomedical Engineering applications, vectors are used to represent the velocity of a flow to further calculate the flow rate and some other related quantities.
3. Vectors play a huge part in industry. For example, in process flow, vectors play a huge part in most calculations.
History
The discovery and use of vectors can date back to the ancient philosophers, Aristotle and Heron. The theory can also be found in the first article of Newtons Principia Mathematica. In the early 19th century Caspar Wessel, Jean Robert Argand, Carl Friedrich Gauss, and a few more depicted and worked with complex numbers as points on a 2D plane. in 1827, August Ferdinand published a book introducing line segments labelled with letters. he wrote about vectors without the name "vector".
In 1835, Giusto Bellavitis abstracted the basic idea of a vector while establishing the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent (meaning equal length). He found a relationship and created the first set of vectors. Also in 1835 Hamilton founded "quaternions", which were 4D planes and equations with vectors.
William Rowan Hamilton devised the name "vector" as part of his system of quaternions consisting of three dimensional vectors.
Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today.
VPython was released by David Scherer in the year 2000. He came up with the idea after taking a physics class at Carnegie Mellon University. Previous programs only allowed for 2D modeling, so he took it upon himself to make something better. VPython, also known as Visual Python, allows for 3D modeling.
See also
External links
Here is a link on more mathematical computations on vectors: [1]
Here is a link on more computational work with vectors: [2]
Further Reading
Vector Analysis by Josiah Willard Gibbs
Introduction to Matrices and Vectors by Jacob T. Schwartz