Simple Harmonic Motion
Claimed for editing by Elton Leander Pinto 10/29/2018
Simple harmonic motion is an approximation that ignores friction and air resistance. Although this assumption can often not be made in everyday calculations, simple harmonic motion can approximate these otherwise complicated situations, fairly well. Simple harmonic motion can be used to estimate many systems including spring-mass systems and the swinging of a pendulum in certain instances which will be explained in further detail below. This Wiki Page will discuss simple harmonic motion which is discussed in detail in Chapter Four: Contact Interaction.
The Main Idea
Simple harmonic motion is a periodic motion, a motion that is repeated over some time interval. This periodic motion has a restoring force, a force that is always working to return the system to equilibrium position, that is proportional and opposite to displacement. Due to this as the system gets farther from equilibrium position the larger the force is to return it to equilibrium position. When no friction or air resistance is present the system will continue to oscillate as the restoring force decreases as the object gets closer to equilibrium position until the force reaches zero, but at which point the particle continues due to its initial momentum until passes equilibrium position. Then the restoring forces increases in the opposite direction until the momentum is changed enough to change the direction of the particle and the process repeats. A common example of simple harmonic motion is an undamped spring-mass system, or one that does not proceed to rest due to friction or another dissipative force. 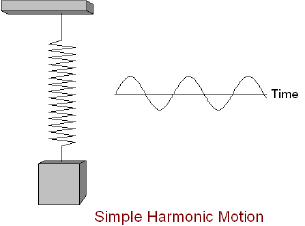
A Mathematical Model
The force of this system can be found using [math]\displaystyle{ \vec{F}={-K_{s}}*s*\vec{Lhat} }[/math] where [math]\displaystyle{ s=L-{L_{o}} }[/math]. This equations stems from Newton's Second Law and Hooke's Law which is a first order linear approximation for forces acting on an elastic system, such as a spring. The solution to this differential equation is [math]\displaystyle{ x=Acos(ωt) }[/math] where [math]\displaystyle{ ω=√({K_{s}}/m) }[/math]. From this equation we can determine that the period for this function, or the time it takes an object to make one complete cycle of motion, to be [math]\displaystyle{ T=2π/ω }[/math].
A Computational Model
Click here to see a spring-mass system displaying simple harmonic motion in vPthyon
Examples
Simple
Problem: A spring has a restoring force of 300 N when it is stretched -.2m. What is the spring's constant [math]\displaystyle{ {K_{s}} }[/math]. in N/m?
Solution:[math]\displaystyle{ F={-K_{s}}*s }[/math]
[math]\displaystyle{ {-K_{s}}=F/s }[/math]
[math]\displaystyle{ {-K_{s}}=300N/-.2m }[/math]
[math]\displaystyle{ {K_{s}}=1500N/m }[/math]
Middling
Problem: What is the oscillation period of a spiring with spring constant 15N/m with a 30 kg mass attached?
Solution: [math]\displaystyle{ T=2π/ω }[/math] or [math]\displaystyle{ T=2π√(m/{K_{s}}) }[/math]
[math]\displaystyle{ {K_{s}}=15N/m) }[/math] and [math]\displaystyle{ m=30kg }[/math]
[math]\displaystyle{ T=2π√(30kg/15N/m) }[/math]
[math]\displaystyle{ T=8.88 seconds }[/math]
Difficult
Problem: A spring with spring constant 18 N/m has mass of 2 kg is attached to it. The mass is then displaced to x = 2 . How much time does it take for the block to travel to the point x = 1?
Solution:
[math]\displaystyle{ x=Acos(ωt) }[/math]
[math]\displaystyle{ x/A=cos(√({K_{s}}/m)t) }[/math]
[math]\displaystyle{ 1/2=cos(√(18N/m/2kg)t) }[/math]
[math]\displaystyle{ cos^{-1}(1/2)=3t }[/math]
[math]\displaystyle{ t=.35seconds }[/math]
Connectedness
One interesting application of simple harmonic motion is its ability to approximate the interatomic vibration of molecules which I find very interesting as an Earth and Atmospheric Science major, trying to better understand our environment and how the molecules it is made up of interact. I have always been very intrigued by the composition and interactions of molecules and this approximations brings me another step closer to understanding how our world works. An interesting industrial application of simple harmonic motion is its approximation of a car running on worn down shock absorbers.
History
Thomas Hooke, an English scientist, created Hooke's Law in 1660 while working on his invention the watch-spring. In the 1660s Hooke gained the title of curator of the Royal Society where he led top experiments for the society. The watch-spring Hooke was working on was one of the first capable of determining longitude at sea by using a spring in simple harmonic motion which has a tendency resist disturbances such as the shakes that could occur while at sea.