Static Friction
claimed by: jfitton3 Short Description of Topic
The Main Idea
Friction is the resistance to motion between two objects. It is proportional to the force that pushes the two surfaces together and the roughness of the surface. Static friction is the friction between two objects that are not moving. Static friction between the two objects will increase to oppose motion until it reaches a certain point in which the objects move. This point of motion is defined by the coefficient of static friction which is generally greater than the coefficient of kinetic friction.
A Mathematical Model
Friction is defined by the formula:
- [math]\displaystyle{ {F}_{friction} = {μ}{F}_{normal} }[/math]
Where [math]\displaystyle{ {μ} }[/math] is the coefficient of friction between the two objects and [math]\displaystyle{ {F}_{normal} }[/math] is the normal force between the two surfaces.
Static friction is the maximum force just before the two objects enter into motion and it is related to the coefficient of static friction. It is defined as follows:
- [math]\displaystyle{ {F}_{max,f} = {μ}_{static}{F}_{normal} }[/math]
Where [math]\displaystyle{ {μ}_{static} }[/math] is the coefficient of static friction and [math]\displaystyle{ {F}_{normal} }[/math] is the normal force between the two surfaces. If the net force exerted on the objects exceeds the F_max the objects start to move. So, the object will begin to move against the direction of the static frictional force if:
- [math]\displaystyle{ {F}_{object} \gt {F}_{max,f} }[/math]
As seen in this diagram, static friction will increase as the applied force to an object increases as well. Eventually, the maximum static frictional force will be reached if the applied force continues to increase. Once this maximum value is reached, the object will begin to move. Then, a kinetic frictional force will begin acting on the object instead which is a relatively constant value regardless the applied force (as long as the object is moving). However, this kinetic frictional force will almost never be greater than the maximum static force because the coefficient of kinetic friction is almost always going to be less than the coefficient of static friction. It wouldn't really make sense if the force required to keep an object moving was greater than the force required to start moving an object from rest.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Basic Example
There is a box on top of a table and is not moving. The box has a mass M and the coefficient of static friction between the box and the table is [math]\displaystyle{ {μ}_{static} }[/math]. What is the frictional force?
The way to solve this problem is to recognize that the box itself is not moving. Therefore, one can deduce that the frictional force has to be static, and the coefficient of static friction can then be used. The static friction force is calculated as follows:
- [math]\displaystyle{ {F}_{friction} = {F}_{N}{μ}_{static} }[/math]
Take notice that [math]\displaystyle{ {F}_{N} }[/math] is equal to [math]\displaystyle{ {F}_{grav} }[/math] which is as follows:
- [math]\displaystyle{ {F}_{grav} = {M}{g} }[/math] where
- [math]\displaystyle{ {g} = {9.81 m/}{s^2} }[/math]
So, the static friction can be simplified to the final equation:
- [math]\displaystyle{ {F}_{friction} = {M}{g}{μ}_{static} }[/math]
This is only a very basic example to show how static friction is calculated.
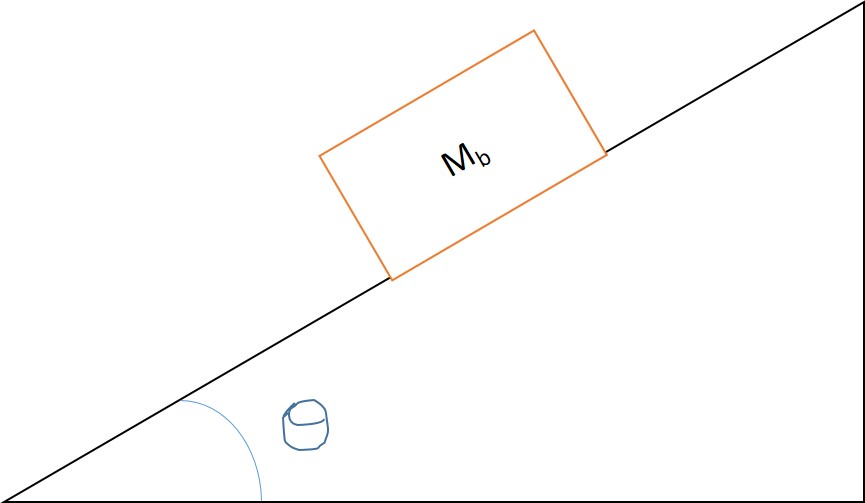
Incline Example
There is a box resting on an incline plane with a mass M_b. The coefficient of static friction between the box and the ramp is μ_s. The box isn’t moving, what is the friction force?
Solution:
To solve the problem the first step required is to identify the free body diagram:
The next step is to calculate the Y component of the F_grav . That will be equal to the F_N .
- [math]\displaystyle{ {F}_{N} = {F}_{grav}{sinθ} }[/math]
- [math]\displaystyle{ With {F}_{grav} = {9.81}{M}_{b} }[/math]
The final step is to utilize the formula for static friction and the calculated F_N:
- [math]\displaystyle{ {F}_{friction} = {F}_{N}{μ}_{s} }[/math]
That solves the problem.
Difficult Example
There is a crate of mass 20 kg sitting on a 40-degree inclined ramp that must be pulled to the top of the ramp to be loaded on a truck for delivery. A worker begins applying a force [math]\displaystyle{ {F}_{T} }[/math] to the crate by pulling on a rope attached to the crate at a 30-degree angle above the incline. If the coefficient of static friction [math]\displaystyle{ {μ}_{s} }[/math] is 0.27, what tension force must the worker apply to the crate in order to begin moving the crate up the ramp?
To begin solving this problem, we must draw a free body diagram in order to easily set up our force equations in order to solve for the tension force. We are going to set the x axis as the hypotenus of the incline and the y axis as the perpendicular to the incline hypotenuse. This should make it easier to break forces up into components. So, the FBD should look something like this:
Now, these forces can be further broken up into x and y components for two separate force equations:
With this new diagram, we can set up the equations for the forces in the x direction and the y direction. We can set both of these equations equal to zero because the crate still isn't moving, so acceleration is zero based on the equation [math]\displaystyle{ {F} = {M}{a} }[/math].
Forces in the x direction:
- [math]\displaystyle{ {F}_{T}{cos(30)} - {F}_{s} - {Mgsin(40)} = {0} }[/math]
Forces in the y direction:
- [math]\displaystyle{ {F}_{N} + {F}_{T}{sin(30)} - {Mgcos(40)} = {0} }[/math]
In order to solve for the applied tension force, we must get [math]\displaystyle{ {F}_{s} }[/math] in terms of known values. Therefore, we must use the coefficient of static friction to solve for this static frictional force in terms of mass, g, coefficient of friction, and the angles given. To do this, we can use the equation of the forces in the y direction to plug in a term for [math]\displaystyle{ {F}_{N} }[/math]:
- [math]\displaystyle{ {F}_{s} = {μ}_{s}({Mgcos(40)} - {F}_{T}{sin(30)}) }[/math]
This can then be plugged back into the equation for the forces in the x direction:
- [math]\displaystyle{ {F}_{T}{cos(30)} - {μ}_{s}({Mgcos(40)} - {F}_{T}{sin(30)}) - {Mgsin(40)} = {0} }[/math]
Then just isolate [math]\displaystyle{ {F}_{T} }[/math] in terms of the values given in the problem:
- [math]\displaystyle{ {F}_{T} = \frac{{μ}_{s}{Mgcos(40) + Mgsin(40)}}{cos(30) + {μ}_{s}{sin(30)}} }[/math]
Just plug in the values and solve for [math]\displaystyle{ {F}_{T} }[/math]:
- [math]\displaystyle{ {F}_{T} = \frac{(0.27)(20)(9.8)cos(40) + (20)(9.8)sin(40)}{cos(30) + (0.27)sin(30)} = {166.36 N} }[/math]
So, the crate must be pulled with a tension force of 166.36 N in order to overcome static friction and begin pulling the crate up the ramp to the truck.
Real Life Application
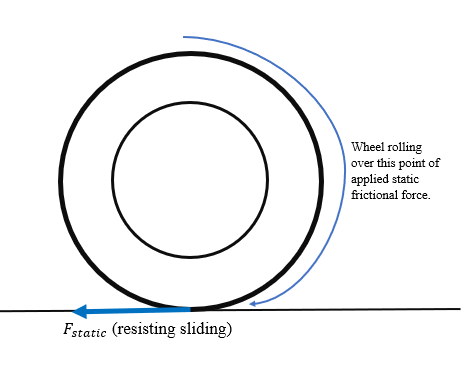
Static friction is a much more important Physics concept than most people think because this static friction plays such a big roll in so many different systems. For example, wheels are able to rotate solely due to static friction because it prevents the wheel from "slipping" with the surface that it makes contact with. The ground applies a static frictional force to the wheel at the point of contact so that the wheel will "roll" over that point without truly spinning.
Static friction can also be seen elsewhere such as walking and running which is achieved through the static friction between our shoe and the ground. The friction itself allows us to push forward using the static friction between our shoe and the ground as a pivot.
Overall, static friction is a relatively basic Physic's concept that plays a big role in our everyday life without us truly noticing. Try keeping your eyes open for different systems of motion and how static friction might play a role on the movement in that system.
Different types of static friction
When getting into world application, static friction can be seen in many different systems as discussed before. To be specific, some of the most common systems of static friction are skin friction for contact between fluids and the skin, internal friction for deformation of bodies, belt friction for pulley systems with belts wrapping around them, fluid friction for viscosity, and even radiation friction for movement of matter.
It is sometimes difficult to recognize the presence of static friction for complex concepts like fluids and motion of matter, but these are all forms of this static friction at a molecular level where atoms come in contact with each other and prevent one another from passing by or moving.
Regardless, static friction almost always converts energy of a system to thermal energy. Since conservation of energy states energy cannot be created nor destroyed, friction can't just "destroy" energy when acting on an object, but instead causes the system to lose energy by converting energy to thermal energy which is then lost to the surroundings. This thermal energy loss can even be calculated by taking the integral of the frictional force over a distance in which the friction acts on an object:
- <math>{E}_{thermal} =
See also
Look below
Further reading
External links
- A couple of animations[3]
References
The book we used in class was a reference utilized in the creation of this page:
Matter and Interactions 4th edition. Full Citation: Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.