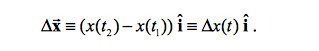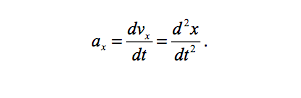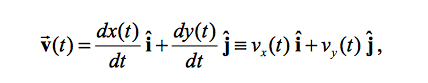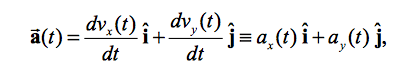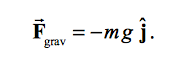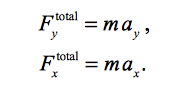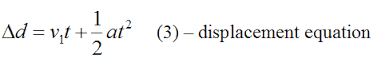Kinematics

This page describes the field of kinematics and presents some of the most important kinematic equations.

The Main Idea

The field of kinematics is the study of motion from a mathematical rather than physical point of view. More specifically, it studies the relationships between time and the position, velocity, and acceleration of particles, without regard for the forces that cause the acceleration. Often, kinematics are used in combination with other branches of physics to predict the motion of an object at different points in time. For example, non-kinematic equations might be used to learn about the magnitude and direction of a force acting on a particle, and about the acceleration that the particle undergoes as a result. Then, kinematic equations might be used to calculate the position of the particle as a function of time based on the acceleration found.

A Mathematical Model

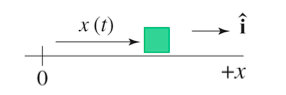
In order to construct a mathematical model of motion, it is important to understand that position can be represented as a vector quantity, having both direction and magnitude. First, let's consider an object moving in one dimension, on per se, the x-axis. The following function (on the left) models the object's position as a function of time, as depicted in the graph pictured to the right.

To construct a function x(t), it is important to understand change in time. Change of time is modeled by the final time observed minus the initial time observed, as seen in the following equation.

Secondly, we need to determine a functions displacement over a period of time. Displacement is described as an objects change in position, as shown in the following equation.

If you divide an object's displacement over a period in time, the result is average velocity, which is also a vector quantity. Instantaneous velocity is a function of time, which models an objects movement relative to a frame of reference, and is the first derivative of displacement with respect to time. Velocity is subject to change over time. This is known as acceleration. Imagine a time when when you were riding in a car, and the driver took off from rest. Acceleration is mathematically modeled as an objects change in velocity over a period of time, or in calculus as the first derivative of velocity with respect to time (instantaneous acceleration).

In multi-dimensions, motion can be described in a similar manner, using the unit vectors i, j, and k.

The multi dimensional acceleration vector a is modeled similarly.

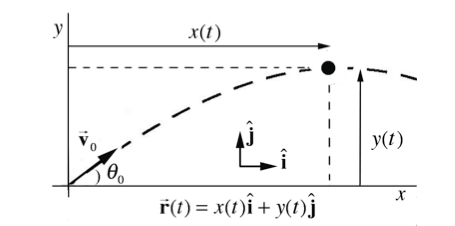
The introductory study of kinematics is often centered around projectile motion problems. Consider the motion of a body that is release at time t = 0 with an initial velocity v at height h above the ground. To analyze problems of this type, choose coordinates with the y-axis in the vertical direction with j pointing upwards and the x-axis in the horizontal direction with i pointing in the direction the object is moving horizontally. Choose the origin to be the point where the object is released. The following figure depicts this coordinate system of the object at time t.

To conclude our study of motion, the fundamental concepts of Force are explored. The only force acting on objects is the gravitation attraction between the object and the earth. The force acts downward with a magnitude of mg, where m is equal to mass, and g is equal to the acceleration of gravity (9.81 m/s^2). Newton's second law states that the net force on an object is a product of the object's mass and its acceleration vector a. The components in the x and y direction can be evaluated individually in this vector equation.

The following equations will be useful in solving problems related to kinematics.

A Strategy for Solving Kinematics Problems

1. Draw a figure of the given situation

2. Identify the principle that applies to the problem

3. Identify the given information and variables

4. Determine the unknown information need to be found from known information.

6. Substitute known values into the necessary equation and follow the mathematical process necessary.

7. Check your answer and indicate appropriate units.

Examples

Easy

An airplane accelerates down a runway at 3.20 m/s2 for 32.8 s until is finally lifts off the ground. Determine the distance traveled before takeoff.

Solution: d=1720 m

Using the following formula

Medium

A person throws a stone at an initial angle θ = 45 from the horizontal with an initial speed of v =20m⋅s-1. The point of release of the stone is at a height d=2m above the ground. You may neglect air resistance. a) How long does it take the stone to reach the highest point of its trajectory? b) What was the maximum vertical displacement of the stone? Ignore air resistance.

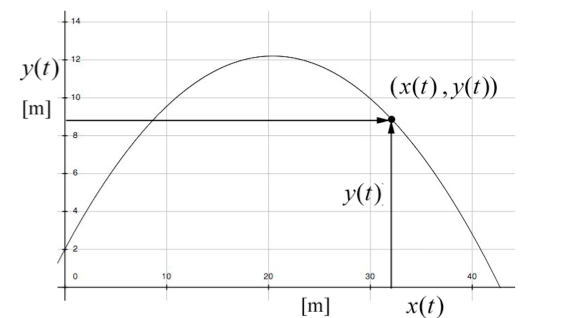
Solution: Choose the origin on the ground directly underneath the point where the stone is released. We choose upwards for the positive y-direction and along the projection of the path of the stone along the ground for the positive x-direction. Set t = 0 the instant the stone is released. At t = 0 the initial conditions are then x0 = 0 and y0 = d . The initial x- and y-components of the velocity are given by Eqs. (5.1.5) and (5.1.6). At time t the stone has coordinates (x(t), y(t)) . These coordinate functions are shown in the following image:

Difficult

A person is standing on a ladder holding a pail. The person releases the pail from rest at a height h1 above the ground. A second person standing a horizontal distance s2 from the pail aims and throws a ball the instant the pail is released in order to hit the pail. The person releases the ball at a height h2 above the ground, with an initial speed v0 , and at an angle θ0 with respect to the horizontal. You may ignore air resistance. a) Find an expression for the angle θ0 that the person aims the ball in order to hit the pail. b) Find an expression for the height above the ground where the collision occurred as a function of the initial speed of the ball v0 , and the quantities h1 , h2 , and s2 .

Connectedness

Kinematics is at the core of all concepts in physics. Understanding the interaction between forces and how these interactions translate to motion, leaves nearly infinite possibilities. There are thousands of real world examples, such as cars, planes, bow and arrows, and essentially everything that moves.

History

Although humans have questioned the nature of motion for thousands of years, Isaac Newton is credited for the advancement of most topics in kinematics. In 1669, Newton was appointed professor of mathematics at Trinity College. In January 1672, he was elected to the Royal Society, a loose organizations of scientists and intellectuals. Shortly thereafter, he presented a paper detailing his discoveries in optics, and developed a rivalry with the scientist Robert Hooke, who harshly criticized Newton's research. This rivalry would percolate throughout the 1670s, as Newton continued to work out the mathematics of gravity, and would again flare up in the mid 1680s when Newton finally published his work, some of which Hooke felt had been stolen from him.

Newton's research was organized into a three-volume book, the Philosophiae Naturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy"), known to posterity as the Principia Mathematica. It set forth Newton's three laws of motion, and proceeded to set forth the theory of gravitation, and back it up with rigorous mathematical proofs. Although the theory had many detractors at first, the scientific community would ultimately embrace it, and the Newtonian world-view would dominate physics until the 20th century.

http://web.mit.edu/8.01t/www/materials/modules/chapter04.pdf

http://www.sparknotes.com/biography/newton/summary.html

http://www.physicsclassroom.com/class/1DKin/Lesson-6/Kinematic-Equations

Kinematics

Contents

The Main Idea

A Mathematical Model

A Strategy for Solving Kinematics Problems

Examples

Easy

Medium

Difficult

Connectedness

History

See also

Further reading

References

Navigation menu