First Law of Thermodynamics
Main Idea
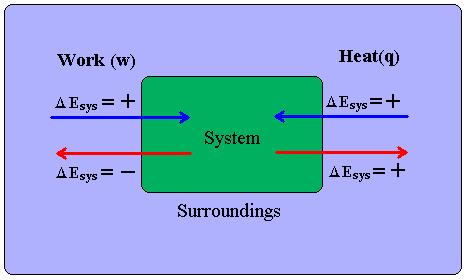
The First Law of Thermodynamics is another way to state Conservation of Energy and The Energy Principle. Hence, if needed, review those topics before diving into The First Law of Thermodynamics. Heat, the transfer of thermal energy, and internal energy, the energy possessed by the constituents of the system, are forms of energy, just like Kinetic Energy and Potential Energy. We can now extend the scope of the Law of Conservation of Mechanical Energy from Work and external potential and kinetic energy to Heat and internal energy. The First Law of Thermodynamics states: although energy comes in various forms, the total quantity of energy stays the same, and the energy disappearing in one form must appear simultaneously in other forms.
Mathematical Model
The First Law of Thermodynamics states:
- The change in internal energy of a system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
- [math]\displaystyle{ \Delta U_{system} = Q + W_{on system} \quad \Delta U_{system} = Q - W_{by system} }[/math]
- [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ W }[/math] are qualitatively energy in transit from the source to the receiver.
- The work done on a system is equal to the negative of the work done by the system:
- [math]\displaystyle{ W_{on system} = -W_{by system} }[/math]
The First Law of Thermodynamics can also be stated in a more general fashion as:
- The change in total energy of the system is equal to the heat added/taken away from the system plus the work done on the system/minus the work done by the system:
- [math]\displaystyle{ \Delta E_{total} = \Delta PE + \Delta KE + \Delta U \quad \Delta E_{total} = Q + W }[/math], where
- [math]\displaystyle{ \Delta PE = }[/math] change in potential energy of the system
- [math]\displaystyle{ \Delta KE = }[/math] change in kinetic energy of the system
- [math]\displaystyle{ \Delta U = }[/math] change in internal energy of the system
- Therefore:
- [math]\displaystyle{ \Delta PE + \Delta KE + \Delta U = Q + W }[/math]
- The quantity [math]\displaystyle{ \Delta PE + \Delta KE }[/math] is usually considered [math]\displaystyle{ 0 }[/math] by The Energy Principle, leading to the previous equation of The First Law of Thermodynamics..
Computational Model
- Insert Computational Model here
Examples
Simple
Middling
Difficult
Connectedness
History
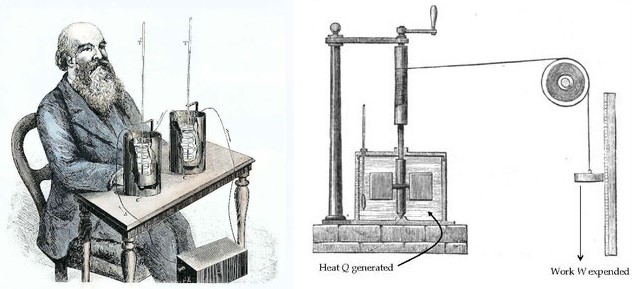
James P. Joule's experiments with Heat and Work made major contributions to the formation of the modern concept of Heat. Joule put certain amounts of mercury, water, and oil into an insulated container and mixed the liquid using a rotating stirrer. He carefully measured how much work was done by the stirrer to the liquid and the change in temperature that the liquid experienced. Joule discovered that for a particular fluid, a fixed amount of Work is required per unit mass in order to raise its Temperature by one degree. Joule established that Heat is a form of energy and that there is a quantitative relationship between Heat and Work.


The science of Thermodynamics originated in the 19th century in order to explain the mechanism of steam engines. The term 'Thermodynamics' means power developed from Heat, and Thermodynamics deals with the relationship between Heat and other forms of energy. One can apply Thermodynamics to a problem, beginning with identifying a body of matter called the system. A system's Thermodynamic state is defined by several macroscopic properties that depend on the fundamental dimensions such as time, temperature, mass, length, etc.
See also
Further reading
External links
References
A Mathematical Model
In the thermodynamics analysis, system is the region in which the process takes place in and the surroundings are everything that the system interacts with. First law is applied to the system and its surroundings, [math]\displaystyle{ ∆ }[/math](Energy of the system) + [math]\displaystyle{ ∆ }[/math](Energy of surroundings) [math]\displaystyle{ = 0 }[/math]
In a closed system, no streams enter nor leave the system and there is no transfer of matter across the boundary of system and its surroundings. All exchange in energy occur as heat and work and total energy change is the net energy transported as heat or work.
[math]\displaystyle{ ∆U = Q+W }[/math] where [math]\displaystyle{ ∆U }[/math] is change in the internal energy , [math]\displaystyle{ Q }[/math] is heat added to the system, and [math]\displaystyle{ W }[/math] is the work done by or done on the system. In other words, change in internal energy is equal to flow of heat into a system plus the work done by or on the system. [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ W }[/math] are energy in transit; they are never stored nor contained in the body. Whereas, potential, kinetic, and internal energy are stored with the matter. While both [math]\displaystyle{ Q }[/math] and [math]\displaystyle{ W }[/math] are path functions, [math]\displaystyle{ ∆U }[/math] is a path-independent state function, which means that it only depends on the current state of the system.
First Law of Thermodynamics may also be written as:
[math]\displaystyle{ E^t }[/math] = Total Energy, [math]\displaystyle{ KE }[/math] = Kinetic Energy, [math]\displaystyle{ PE }[/math]=Potential Energy
[math]\displaystyle{ ∆E^t = ∆KE + ∆PE + ∆U }[/math]
[math]\displaystyle{ ∆E^t = Q + W }[/math]
[math]\displaystyle{ ∆KE + ∆PE + ∆U = Q + W }[/math]
A Computational Model
http://jersey.uoregon.edu/vlab/Thermodynamics/
This virtual experiment gives you visual representation of thermal equilibrium and how it is reached when beginning with different initial conditions.
Examples
Simple
Heat of 5000J is added to a closed system and the internal energy is decreased by 11000J. How much energy is transferred as work?
Solution:
[math]\displaystyle{ ∆U = Q + W }[/math], [math]\displaystyle{ Q= 5000J }[/math], [math]\displaystyle{ ∆U=-11000 J }[/math]
[math]\displaystyle{ -11000J = 5000J + W }[/math]
[math]\displaystyle{ W = -11000J-5000J }[/math]
[math]\displaystyle{ W = -16000J }[/math]
Middling
An egg, initially at rest, is dropped onto a concrete surface and breaks. Treat the egg as the system.
a) What is the sign of [math]\displaystyle{ W }[/math]?
b) What is the sign of [math]\displaystyle{ ∆PE }[/math]?
c) What is [math]\displaystyle{ ∆KE }[/math]?
d) What is [math]\displaystyle{ ∆U }[/math]?
e) What is the sign of [math]\displaystyle{ Q }[/math]?
Solution:
Utilizing [math]\displaystyle{ ∆KE+∆PE+∆U=Q+W }[/math]
a) No work is done on the system + no work is done by the system to the surroundings, thus [math]\displaystyle{ W }[/math] = 0.
b) Egg is falling from a higher surface, which means the elevation is decreased and the sign of [math]\displaystyle{ ∆PE }[/math] is negative (-).
c) Because the egg is at rest for both the initial and final state, [math]\displaystyle{ ∆KE }[/math] = 0.
d) The chemical state of egg does not change (it does not get scrambled), thus [math]\displaystyle{ ∆U }[/math] = 0.
e) From the above equation, the values with zero ([math]\displaystyle{ W }[/math], [math]\displaystyle{ ∆PE }[/math], and [math]\displaystyle{ ∆KE }[/math]) can all be cancelled and [math]\displaystyle{ ∆PE }[/math] would equal [math]\displaystyle{ Q }[/math].
[math]\displaystyle{ ∆PE = Q }[/math]
Because the [math]\displaystyle{ ∆PE }[/math] is negative(-), [math]\displaystyle{ Q }[/math] is also negative.
Difficult
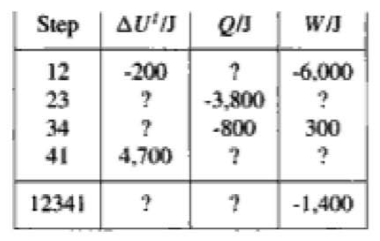
One mole of gas in a closed system undergoes a four-step thermodynamic cycle. Using the below data, determine numerical values for the missing quantities.
Solution:
[math]\displaystyle{ ∆U_t = Q+W }[/math]
step 1 to 2:
[math]\displaystyle{ ∆U_t(12) = -200J, W(12) = -6000J }[/math]
[math]\displaystyle{ Q(12)=∆U_t(12) - W(12) = -200J - (-6000J) = 5800J }[/math]
step 3 to 4:
[math]\displaystyle{ Q(34) = -800J, W(34) = 300J }[/math]
[math]\displaystyle{ ∆U_t(34)= Q(34) + W(34) = -800J + 300J = -500J }[/math]
[math]\displaystyle{ ∆U_t }[/math] is a state function.
That means a [math]\displaystyle{ ∆U_t }[/math] for series of steps that leads back to the initial state must be zero.
The sum of U for all of the steps must be zero.
[math]\displaystyle{ ∆U_t(12341) = 0 }[/math]
[math]\displaystyle{ ∆U_t(41) = 4700J }[/math]
[math]\displaystyle{ ∆U_t(23) = 0 - ∆U_t(12) - ∆U_t(34) - ∆U_t(41) = 0 - (-200J) - (-500J) - 4700J = -4000J }[/math]
Step 2 to 3:
[math]\displaystyle{ ∆U_t(23) = -4000J, Q(23) = -3800J }[/math]
[math]\displaystyle{ W(23) = ∆U_t(23) - Q(23) = -4000J - (-3800J) = -200J }[/math]
[math]\displaystyle{ W(12341) = -1400J }[/math]
[math]\displaystyle{ W(41) = W(12341) - W(12) - W(23) - W(34) = -1400J - (-6000J) - (-200J) - 300J = 4500J }[/math]
Step 4 to 1:
[math]\displaystyle{ ∆U_t(41) = 4700J W(41) = 4500J }[/math]
[math]\displaystyle{ Q(41) = ∆U_t(41) - W(41) = 4700J - 4500J = 200J }[/math]
Connectedness
1. How is this topic connected to something that you are interested in?
- In physics, I've always encountered the subject of "Thermodynamics" with excitement. I always loved to deal with temperatures and mc∆T is the equation that I enjoy utilizing the most. Being able to explain the mechanism of our fingers instantly turning cold as they touch the ice or in reverse, our hands warming up by simply holding a cup of hot cocoa as the flow of heat from a hotter object to colder object is inspring. Plus, there are even specific quantitative relationships that exist between the heat, work, and internal energy and we are enabled to apply them exactly into our daily lives, thus the science of "Thermodynamics" is indeed extremely empowering!
2. How is it connected to your major?
- I major in Chemical Engineering. There are two-semester worth of curriculum dedicated solely to "Thermodynamics" in my major. The fundamental laws of thermodynamics embody mathematical deduction to a network of equations which can be applied in all branches of science and engineering. Chemical engineer provide solutions to wide range of problems and many of them has to do with calculating the heat and work for various physical and chemical processes. Thus, "thermodynamics" is one of the skeletal parts of Chemical Engineering.
3. Is there an interesting industrial application?
- Thermodynamics is relevent in the energy,transportation, petrochemical, and HVAC industries.
See also
Further reading
- Thermodynamics (Dover Book on Physics) by Enrico Fermi
- Engineering Thermodynamics by P. K. Nag
- M. J. Moran and H. N. Shapiro, ‘Fundamentals of Engineering Thermodynamics’, Fourth Edition, Wiley, New York, 2000
- Thermodynamics: An Engineering Approach by Cengel, Ya and Boles, M.A.
- Introduction to Chemical Engineering Thermodynamics, Seventh Edition, by J.M. Smith, H.C. Van Ness, M.M. Abbott
External links
- http://www.scientificamerican.com/article/bring-science-home-reaction-time/
- http://www.physlink.com/Education/AskExperts/ae280.cfm
- http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
- http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
- http://www.wiley.com/college/moran/CL_0471465704_S/thermonet/docs/user/index.html ThermoNet]
- https://www.khanacademy.org/science/physics/thermodynamics/laws-of-thermodynamics/v/first-law-of-thermodynamics-internal-energy Khan Academy: First Law of Thermodynamics
- http://www.ncert.nic.in/html/learning_basket/energy10class/joule's%20experiment.htm
- http://demonstrations.wolfram.com/JoulesExperiment/
- https://www.wolframscience.com/reference/notes/1019b
- http://www.livescience.com/50776-thermodynamics.html
- https://www.youtube.com/watch?v=5yOhSIAIPRE Mechanical Equivalent of Heat
References
- Callen, Herbert B. (1985). Thermodynamics and an Introduction to Thermostatistics. Wiley. p. 5,37.
- http://fineartamerica.com/featured/1-thermodynamics-conceptual-artwork-richard-bizley.html
- http://www.humanthermodynamics.com/Clausius.html
- http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
- http://www.juliantrubin.com/bigten/mechanical_equivalent_of_heat.html
- https://www.grc.nasa.gov/www/k-12/airplane/thermo1.html
- https://www2.estrellamountain.edu/faculty/farabee/biobk/BioBookEner1.html
- http://www2.phy.ilstu.edu/~hmb/phy325/TPCh.7.1(09).pdf
- http://www.shashaiseminar.com/notes/a-level/zimsec/physics/heat-2/
- https://www.asee.org/public/conferences/8/papers/4611/download