Second Law of Thermodynamics and Entropy
Main Idea
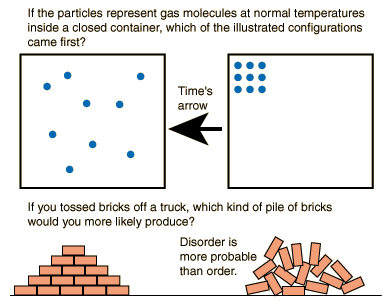
Entropy quantitatively represents the unavailability of a system's Thermal Energy to be converted into mechanical work. The entropy of a system can also be described as the system's level of disorder or randomness. The more entropy a system has, the more random it will be. The Second Law of Thermodynamics states that the entropy of the Universe will always increase over time. The second law also states that the change in the entropy of the Universe will never be negative. Essentially, through the discovery that Heat can not spontaneously flow from a colder body to a hotter body, physicists also discovered that it is impossible to complete any physical process without the loss of some usable energy. As time goes on, randomness can only increase.
Mathematical Model
In Boltzmann's description of entropy, entropy is a way to describe the number of different possible micro-states within a macro-state (specified Temperature, Pressure, Volume, etc.). This leads to the popular idea that greater entropy means greater disorder in a system. Formally, Boltzmann's theory says:
- [math]\displaystyle{ S = -k_{B}\sum_{i} p_{i}\ \text{log}(p_{i}) }[/math], where
- [math]\displaystyle{ S = }[/math] is the entropy of the macro-state
- [math]\displaystyle{ k_{B} = 1.38065 \times 10^{−23} \ \frac{J}{K} }[/math] (Boltzmann's constant)
- [math]\displaystyle{ p_{i} = }[/math] the probability that the micro-state is in the [math]\displaystyle{ i\text{-th} }[/math] micro-state
- [math]\displaystyle{ \sum_{i} = }[/math] the summation over all possible micro-states
However, it is usually assumed that each micro-state is equally probable:
- [math]\displaystyle{ \Omega = }[/math] the number of different, possible micro-states
If each possible micro-state is assumed to be equally probable, then:
- [math]\displaystyle{ S = -k_{B}\sum_{i} p_{i}\ \text{log}(p_{I}) = -k_{B}\sum_{I}^{\Omega} \frac{1}{\Omega} \ \text{log}\left(\frac{1}{\Omega}\right) = -k_{B} \ \text{ln}(\Omega) }[/math]
Also, The Second Law of Thermodynamics states the entropy of an isolated system will always stay the same (if a reversible process occurs) or increase (if an irreversible process occurs), as a system tends towards thermodynamic equilibrium.
- In an idealized closed system, where an infinitesimal change in entropy occurs due to an infinitesimal transfer of Heat, the following is true:
- [math]\displaystyle{ dS = \frac{\delta Q}{T} }[/math], where
- [math]\displaystyle{ dS = }[/math] an infinitesimal change in entropy of the system
- [math]\displaystyle{ \delta Q = }[/math] an infinitesimal transfer of Heat to the or from the system
- [math]\displaystyle{ T = }[/math] the Temperature of the system in equilibrium and the surroundings which supply or receive the Heat
- In a more realistic setting, a closed system could go through an irreversible process. If so, the following is true:
- [math]\displaystyle{ dS \gt \frac{\delta Q}{T_{surr}} }[/math], where
- [math]\displaystyle{ T_{surr} = }[/math] the Temperature of the surroundings
- In general then, for any system in the Universe, including the Universe itself, the following holds true:
- [math]\displaystyle{ dS \ge \frac{\delta Q}{T} }[/math]
Clausius' Theorem states "Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time." In his theorem he describes entropy mathematically as:
- [math]\displaystyle{ \Delta S \ge \int \frac{\delta Q}{T} }[/math]
Note the equality only holds if the process is reversible.
Computational Model
Examples
Simple
- give some values of integrals and ask for realisticness and possibility.
Middling
- give number of different micro-states of a system, ask for entropy
- change number of micro-states, ask for entropy again
- ask for change in entropy, is this possible naturally?
Difficult
Connectedness
How is this topic connected to something that you are interested in?
- For someone who loves to cook as much as I do, entropy plays a surprisingly large role. For example, entropy is the reason that Crystal Light powder dissolves in water. Over time, the particles spread and spread because the more spaced out they are, the more disorderly they are. And as we know, disorder must increase with time.
How is it connected to your major?
- As an Industrial and Systems Engineering major, a lot of the work I do will be designing production plants to be as efficient as they can possibly be. Understanding the concept of entropy and that no physical process can be completed without the loss of energy will help me to be able to account for that energy loss in my plans so that I can minimize the amount of inefficiency that occurs. To understand that disorder is inherently more probable than order can help me be aware of more possible outcomes.
Is there an interesting industrial application?
- The Second Law of Thermodynamics is especially used in any industry making insulated products. Well, it is not "used" so much as it is fought against. Using the specifics of The Second Law of Thermodynamics, companies who make thermoses or lunch boxes or insulation need to understand entropy and The Second Law to learn how to best fight Heat dissipation so that they can keep hot things hot and cold things cold.
History
Contributors in the Development of The Second Law of Thermodynamics:

- Nicholas Léonard Sadi Carnot (1 June 1796 – 24 August 1832)
- Considered to be the father of Thermodynamics
- Major Scientific Contributions:
- Carnot heat engine
- Carnot theorem
- Carnot efficiency
- His research was centered around learning if the work available from a heat source was limited, and whether the efficiency of a heat engine could be improved upon by replacing steam with a different substance

- Rudolf Clausius ( 2 January 1822 – 24 August 1888)
- German Physicist
- Developed the Clausius statement, which states that in general, heat can not flow spontaneously from a low temperature to a high temperature
- Wrote a famous paper titled "On the Moving Force of Heat and the Laws of Heat which May be Deduced Therefrom"
- Pointed out differences between the concept of conservation of energy
- Stated that assumptions about the Caloric theory were incorrect
- Presented the idea of Entropy and named it as such
- Was known for taking a mathematical approach to physics

- William Thompson (26 June 1824 – 17 December 1907)
- Also known as First Baron Kelvin
- Mathematical physicist and engineer
- Formulated the Kelvin Statement, which states that there is no way to convert all of the energy in a given system into work without losing energy
- Developed the vortex theory of the atom
- In addition to his contributions to thermodynamics, he also created the Kelvin scale

- Constantin Carathéodory (13 September 1873 – 2 February 1950)
- German mathematician of Greek origin
- Principle of Caratheodory
- Took on thermodynamics with a mathematical axiomatic foundation
- Created his own version of the Second Law of Thermodynamics by stating that "In the neighborhood of any initial state, there are states which cannot be approached arbitrarily close through adiabatic changes of state."
- Used differential equations and Pfaffian expressions to prove the existence of entropy
See also
Further reading
External links
References
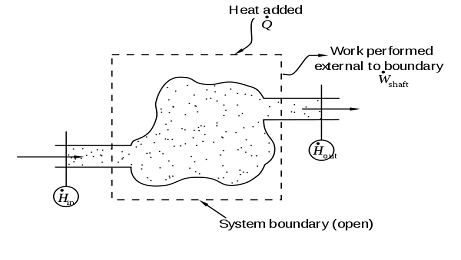
Entropy in Open Systems
The second law of thermodynmaics states the entropy of the universe must be increasing. However, this does not mean that the entropy of a system must necessarily increase. This can be done by manipulating the definition of the system. Consider the following example of an ice cube tray filled with water placed in a freezer.
System 1: ice cube tray
In this system, we find that energy is leaving the system. In fact, it appears that energy is flowing from cold to hot, meaning that the freezer (the surroundings) must be doing negative work on the system. Looking at the equation from the second law of thermal dynamics, we can deduce that ΔQ is negative since energy is leaving the system (negative work is done). This signifies that the change in entropy is negative, as T is always positive (kelvin). With neither the energy principle nor the second law of thermodynamics satisfied, we find that this open system must be expanded in order to satisfy these fundamental principles.
System 2: ice cube tray and freezer
When the freezer is included in the system, the transfer of thermal energy becomes 0. This is due to all the thermal energy flowing from the ice cube tray into the freezer, meaning the ice cube tray loses thermal energy while the freezer gains thermal energy. Thus, since there is no loss of energy to the surroundings (ΔQ = 0), we find that the entropy stays the same. However, the system can once again be expanded to satisfy the second law of thermodynamics. In reality, energy would flow from the surroundings into the freezer. For this case, the freezer is perfectly insulated and no energy or matter can pass into the freezer from the surroundings.
System 3: the universe
Consider the universe as the system. Energy flows to the freezer (despite insulation, the temperature of the freezer will inevitably increase). Therefore, ΔQ is positive. Meaning that the entropy must increase. Consequently, we find that the energy principle is still satisfied, as the energy is transformed, and not created nor destroyed.
From the examples above, the following statement can be deduced: 'If the entropy of one system is decreasing, the entropy of another must be increasing.'
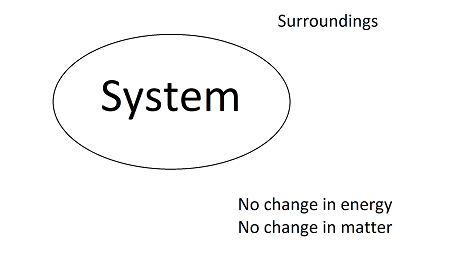
Entropy in Isolated Systems
By definition, entropy in an isolated system can never decrease. An isolated system is defined as a system in which neither energy nor matter can pass to the surroundings. Consider the ice cube tray example from above. When considering just the ice cube tray as the system, it can be noted that just the ice cube tray cannot be an isolated system. This is because energy or matter could easily flow from the surroundings into the ice cube tray, with the surroundings being the freezer. The other two systems, the freezer and the universe, can be considered isolated systems. The change in entropy is either zero or increasing for both systems respectively.
The difference between an open system and an isolated system is that work can be done by the surroundings onto the system in an open system, while the opposite is true for an isolated system. Work, loosely defined, causes a positive or negative change in the energy of the open system. In most cases, energy transforms into a less usable state. Consder a person running for example. Energy begins as chemical energy before transforming into kinetic motion energy until it ultimately dispels as thermal energy. Thermal energy is often the final resting place for other forms of potential and kinetic energy. It is the most disorderly form of energy, and therefore in any isolated system, including the universe in its entirety, the entropy increases over time as more and more energy enters a more disordered form. A system must either be open or isolated.
History
See also
Energy Transfer due to a Temperature Difference