Speed and Velocity
by Matt Schoonover
Speed and Velocity
Speed and velocity are used fairly interchangeably in casual conversation, but when it comes to physics the two can mean vastly different things. Velocity has direction and therefor a vector quantity. Speed is the scalar form of velocity and therefor has no direction.
The most basic equation for velocity is v=d/t. From this comes the average velocity equation of v ⃗_avg=(r ⃗_f-r ⃗_i)/(t_f-t_i ).
The equation for speed is speed=|v ⃗ |=√(〖v_x〗^2+〖v_y〗^2+〖v_z〗^2 ).
A Mathematical Model
In order to find the velocity of an object one must find the change in distance over the change in time. In order to find the speed of an object one must find the magnitude of the velocity. Both are measured in meters per second.
A Computational Model
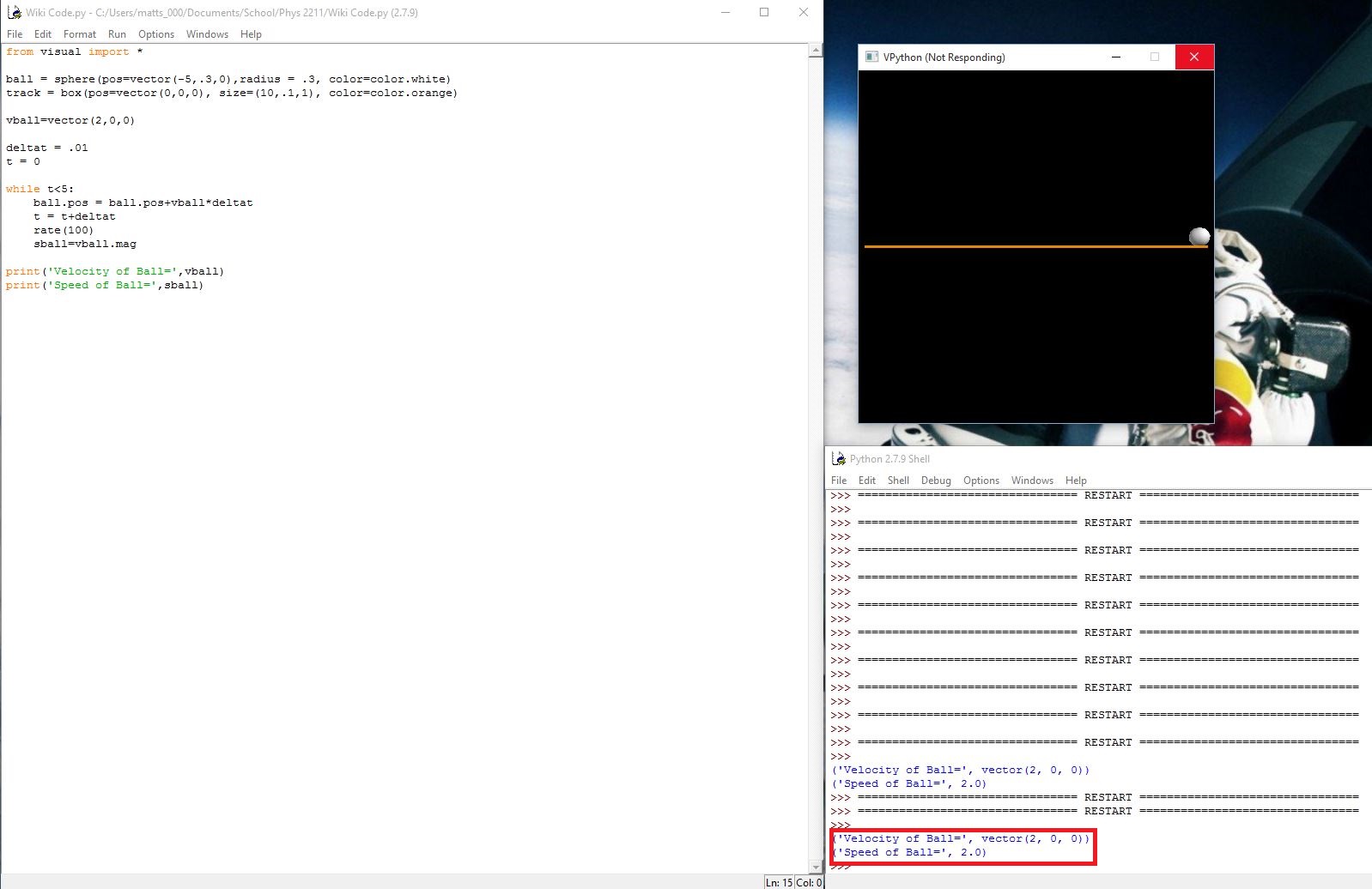
To help demonstrate the difference between the two, I wrote some simple code to model the motion of a ball moving on a track.
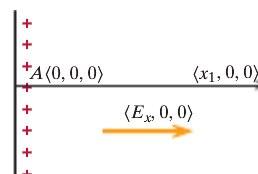
In the first picture, the velocity is only in one direction, so the speed and velocity are the same.
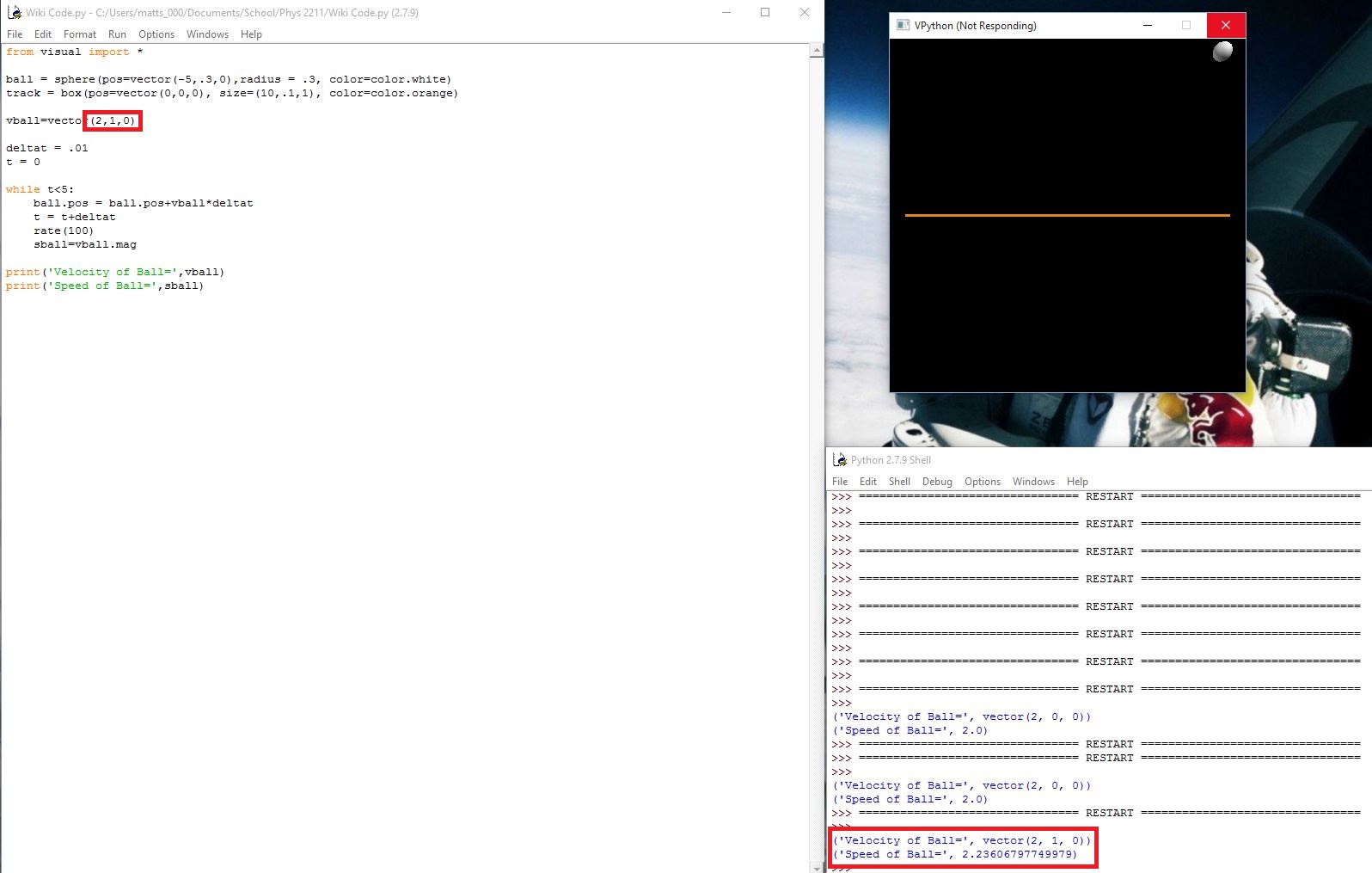
However, in the second picture, the velocity is in the x and y direction, so the speed and velocity are not the same.
Simple Example
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].
Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]
Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.
The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].
The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].
Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page