Curly Electric Fields

Written by Miranda Fyfe

The Curly Electric Field is the non-Coulombic result of a changing current and time-varying magnetic field.

Definition

In the case where current in a solenoid is constant and magnetic force is likewise constant in time, it can be observed that the magnetic and electric forces experienced by some moving charge outside the solenoid are essentially zero.

However, in the situation where current in the solenoid is changing and magnetic force is thereby time-varying, a Curly Electric Field can be observed.

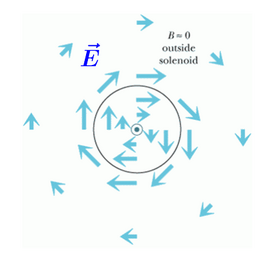
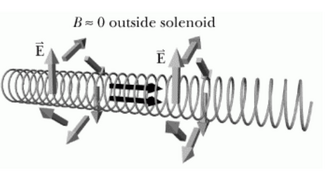
*The **curly electric field** curls around the axis of the solenoid*

*Outside of the solenoid, magnetic field is still virtually zero, but the curly electric field can be observed both inside and outside of the solenoid*

Proportionality

This electric field is proportional to the rate of change of the magnetic field [math]\displaystyle{ ( \frac{\delta B}{\delta t} ) }[/math].

Inside the solenoid

Curly electric field is proportional to distance from the solenoid axis, r.

Outside the solenoid

Curly electric field is proportional to 1/r, with the field decreasing as distance from the axis increases.

The Non-Coulomb Curly Electric Field

Read more about the Non-Coulomb Electric Field

Coulomb Electric Field

Any electric field in accordance with Coulomb's law is said to be a Coulomb electric field.

Coulomb's Law: [math]\displaystyle{ \vec{E} = \frac{1}{4{\pi}{{\epsilon}_0}} \frac{q}{r^2} \hat{r} }[/math]

Non-Coulomb Electric Field

An electric field associated with a time-varying magnetic field, i.e. the curly electric field.

Effect on charges

The curly electric field has a standard effect on charges [math]\displaystyle{ ( \vec{F} = q\vec{E} ) }[/math]

Because the curly electric field deals with non-stationary charges and the magnetic field and current are time-variant, the curly electric field is a Non-Coloumb Electric Field.

Direction of Curly Electric Field

Faraday's Experiment

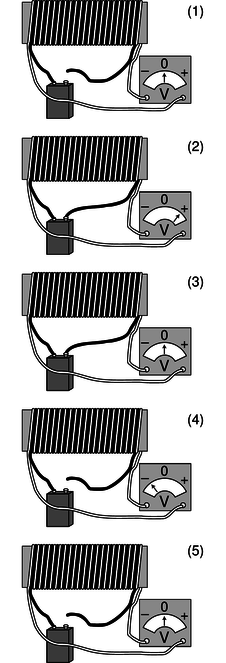
In 1831, Michael Faraday conducted an experiment which proved magnetic fields could be produced by electric currents. The experiment involved connecting a battery to a large coiled wire, and measuring the effects with a voltmeter. Faraday recorded effects both upon first connecting the battery and when initially disconnecting it the later of which was found surprising.

Because an effect could only be gauged when the magnetic field was changing, it was concluded that this effect was proportional to [math]\displaystyle{ ( \frac{\delta B}{\delta t} ) }[/math]

Finding the Direction

Implementing this proportion takes the process a step further; a Right Hand Rule can be utilized to pinpoint the direction of the curly electric field as follows:

Point the thumb of the right hand in the direction of [math]\displaystyle{ ( - \frac{\delta B}{\delta t} ) }[/math] , and curl the fingers in the direction of the curly electric field.

*The right hand rule for finding the direction of curly electric field*

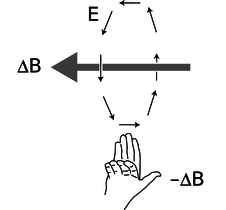
For each of the following four situations, the right hand rule can be used to determine direction of curly electric field.

Magnetic field out of the page and increasing [math]\displaystyle{ \rightarrow }[/math] Clockwise curly electric field
Magnetic field into the page and increasing [math]\displaystyle{ \rightarrow }[/math] Counterclockwise curly electric field
Magnetic field out of the page and decreasing [math]\displaystyle{ \rightarrow }[/math] Counterclockwise curly electric field
Magnetic field into the page and decreasing [math]\displaystyle{ \rightarrow }[/math] Clockwise curly electric field

External Links

References

Matter and Interactions, Vol. 2 by Chabay and Sherwood
http://physwiki.ucdavis.edu/Fundamentals/11._Electromagnetism/11.5_Induced_Electric_Fields
http://www.phy.uct.ac.za/courses/opencontent/phy1004w/1004W%20EM%2022.pdf