Gravitational Potential Energy

This topic covers Gravitational Potential Energy.

Gravitational Potential

Gravitational Potential energy belongs to a pair of objects in a system (for instance a ball+ Earth system, galaxies of stars interacting gravitationally) and is equal to the work done against gravity. This potential energy is the energy associated within the particles inside a system and is not the same as rest or kinetic energies of the individual particles. Traditionally potential energy is represented by the symbol U and this page describes specific examples in which U is equal to the gravitational energy learned about in earlier pages to be approximately mg near the surface of the Earth or [math]\displaystyle{ F = - G \frac{m_1 m_2}{r^2}\ }[/math]
where:

F is the force between the masses;
G is the gravitational constant (6.674×10⁻¹¹ N · (m/kg)²);
m₁ is the first mass;
m₂ is the second mass;
r is the distance between the centers of the masses.

The latter case is distance dependent and can be derived since force is the negative gradient of U. The negative indicates that potential energy decreases as particles get closer together

A Mathematical Model

In a system composed of two objects that are interacting with gravitational potential: [math]\displaystyle{ F = - G \frac{m_1 m_2}{r^2}\ }[/math]
where:

F is the force between the masses;
G is the gravitational constant (6.674×10⁻¹¹ N · (m/kg)²);
m₁ is the first mass;
m₂ is the second mass;
r is the distance between the centers of the masses.

Close to the Surface of the Earth:

[math]\displaystyle{ U = mgh\! }[/math]

where U is the potential energy of the object assuming it is close to the surface of the Earth, m is the mass of the object, g is the acceleration of 9.8, and h is height.

Potential difference is derived to be:

[math]\displaystyle{ \,\Delta U = mg \Delta h.\ }[/math]

[1]

A Computational Model

How do we visualize or predict using this topic?

Graphs are the best mathematical way to represent potential energy. Be low are a few examples of how to draw potential energy graphically.

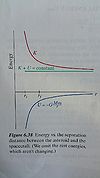
In figure 6.38 to the left, there is a representation of a spacecraft leaving the asteroid. The gravitational potential is negative because the interaction is attractive and by the graph we can see the potential increases with separation.

In the next figure to the right it is important to note as the asteroid gets farther away the kinetic energy will continue to fall and K approaches K+U, but K can not be negative since it involves velocity. When the two objects are far apart U is nearly 0 and K+U is nearly K. This graph is an example of a bound system, with the spacecraft having a smaller initial velocity headed away from the asteroid.

How to Draw Energy graphs

Draw U vs. r for the interaction
At some r where you know K, plot the point
Add that value of K to U so it has the same separation r
Plot K+U at the r value, find K when added to U gives K+U
Sketch K vs. r

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A ball of mass 100 grams is 7m above the ground, initially at rest( Ki=0) When the ball is 4 m above the ground what is the final Kinetic energy? Choose the ball+ Earth system. == First look at the two pictures to the right in order to see the ball+Earth as a system and to see what equations to use. The rest Energy is 0.

[math]\displaystyle{ 0=\Delta K_{(Earth)} + \Delta K_{(ball)} +\Delta U }[/math],

[math]\displaystyle{ 0= 0+(K_{(ball,f)} -0)+ \Delta(mgy) }[/math]

[math]\displaystyle{ 0= K_{(ball,f)} + (0.1 kg)*(9.8 N/M)*(-3 m) }[/math]

[math]\displaystyle{ U_g -2.94J }[/math]

This is used to solve for kinetic energy

[math]\displaystyle{ K_{(ball,f)} = 2.94 J }[/math]

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Ball+Earth system

Middling

In February 2013 a large meteor, whose mass has been estimated to be 1.2x107 kg, fell to Earth near Chelyabinsk, Russia. (This meteor exploded spectacularly at height of about 30 km, doing significant damage to objects on the ground.) Consider a meteor of the same mass falling toward the Earth. Choose the Earth plus the meteor as the system. As the meteor falls from a distance of 1e8 m from the center of the Earth to 1e7 m, what is the change n the kinetic energy of the meteor? Explain the signs of the changes in kinetic and potential energy of the system.

[math]\displaystyle{ U_{(grav)} }[/math] must first be calculated explicitly for each state

[math]\displaystyle{ U_i = G \frac{m_E m_m}{r^2} = -6.7e-11 Nm^2/kg^2 \frac{6e24 kg * 1.2e7 kg m_m}{1e8^2m} }[/math]

[math]\displaystyle{ = -4.82e13J }[/math]

[math]\displaystyle{ U_f = G \frac{m_E m_m}{r^2}= -6.7e-11 Nm^2/kg^2 \frac{6e24 kg * 1.2e7 kg m_m}{1e7^2m} }[/math]

[math]\displaystyle{ = -4.82e14J }[/math]

Both the initial and final values are negative. Seperation decreases so we know that The final potential energy minus the initial is greater than 0. Apply the Energy Principle now to find the final answer.

[math]\displaystyle{ \Delta K_{(meteor)}+(-4.82e14 J - -4.82e13J)=0 }[/math]

[math]\displaystyle{ \Delta K_{(meteor)}=4.34e14J }[/math]

Difficult

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Robot Spacecraft blastoff

A robot spacecraft lands on an asteroid, picks up a sample, and blasts off to return to the Earth; it's total mass is 1500 kg. When it is 200 km from the center of mass of the asteroid, its speed is 5.0 m/s, and the rockets are turned off. At the moment when it has coasted to a distance 500 km from the center of the asteroid, its speed has a decreased to 4.1 m/s. Calculate the mass of the asteroid.

M will be the mass of the asteroid and m will be the mass of the spacecraft.

[math]\displaystyle{ E_{(f)}= E_i + W }[/math]

Mc^2 + K_Mf+ mc^2 + [math]\displaystyle{ K_{(mf)}+ U_{(f)} }[/math]= Mc^2 + K_Mf+ mc^2 + [math]\displaystyle{ K_{(m,i)}+ U_{(i)} + W }[/math]

[math]\displaystyle{ K_{(m,f)}+ U_{(f)}= K_{(m,i)}+ U_{(i)} + 0 }[/math]

[math]\displaystyle{ .5 m v_{(f)}^2 - G \frac{M m}{r_{(f)}}= .5 m v_{(i)}^2 - G \frac{M m}{r_{(i)}} }[/math]

Can factor out the m

[math]\displaystyle{ m (.5 v_{(f)}^2 - G \frac{M }{r_{(f)}})= m(.5 v_{(i)}^2 - G \frac{M }{r_{(i)}} ) }[/math]

[math]\displaystyle{ GM (\frac{1 }{r_{(i)}} -\frac{1 }{r_{(f)}} )= .5 (v_{(i)}^2 -v_{(f)}^2) }[/math]

Connectedness

http://voyager.jpl.nasa.gov/ Nasa uses gravitational energy to get probes to break through the heliosphere as in the voyager mission. Gravitational energy is very important to understand when sending probes to explore planets.
Biochem majors may find this information useful in understanding how chemical potential works.
Actual Application: http://www.forbes.com/sites/startswithabang/2015/11/02/move-over-hubble-gravity-itself-is-the-best-cosmic-telescope-of-all/

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

Newton thought gravitational attraction was caused by mysterious magnetic forces.Einstein rejected this and came up with what we now know as force. Then it was just left to realize that work must be replaced with potential in a system of interacting objects.

References

This section contains the the references you used while writing this page

Media:http://www.physicsclassroom.com/class/circles/Lesson-3/Newton-s-Law-of-Universal-Gravitation Media:http://matterandinteractions.org/

Mathmatical Model and gravity Feild: Media:https://en.wikipedia.org/wiki/Newton's_law_of_universal_gravitation

Gravitational Potential Energy

Contents