Iterative Prediction of Spring-Mass System

Claimed by kgiles7 2015

Edited by Richard Udall June 2019

The spring mass system is one of the classical examples of harmonic motion. The idealized case, where no forces except the spring force are acting upon the system, is the prototypical example of Simple Harmonic Motion. This page will explore less idealized cases, introducing damping, driving, and added gravitational force.

The Main Idea

Added complications bring the spring mass system much closer to a real system than the idealized system we have included before. Since we had to deal with the idealized system using iterative prediction, we will need to deal with this more complex situation using iterative prediction as well. Since our model presented in Fundamentals of Iterative Prediction with Varying Force is fairly general, adding these complications consists of adding new forces, and observing the resultant behaviors. These cases can also be explored analytically using differential equations, but doing so is outside of the scope of this class.

A Mathematical Model

The page Fundamentals of Iterative Prediction with Varying Force lays out the general methods of iterative prediction, but a brief recapitulation is provided here. he Momentum Principle provides a mathematical basis for the repeated calculations needed to predicts the system's future motion. The most useful form of this equation for predicting future motion is referred to as the momentum update form, and can be derived by rearranging the Momentum Principle as shown below:

[math]\displaystyle{ \Delta p = \vec{F}_{net}\Delta t }[/math]

[math]\displaystyle{ \vec{p}_{f} - \vec{p}_{i} = \vec{F}_{net}\Delta t }[/math]

[math]\displaystyle{ \vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}\Delta t }[/math]

Kinematics, expressed in a similarly iterative manner, allows for the determination of the next iteration's position and velocity

[math]\displaystyle{ \vec{v}_{f} = \frac{\vec{p}_f}{m} }[/math]

[math]\displaystyle{ \vec{r}_{f} = \vec{r}_{i} + \vec{v}_{avg}\Delta t }[/math]

Damping

We know from our observations of a pendulum swinging or a spring bobbing that it's periodic motion eventually dies out. This results from dissipative forces present in our environment, such as friction or air resistance. The question of why these are called dissipative will become clear when we learn about Work/Energy, but sufficed to say that they will reduce the amount of motion in the system. A formal derivation of the equations of motion for a damped system will not be considered here, but it is very straightforward to add damping to our computational model. Whenever we calculate the net force on the mass during the iterative process, all we have to do now is add a dissipative force. For air resistance, the standard formula is

[math]\displaystyle{ \vec{F} = -\frac{CAρv^2\hat{v}}{2} }[/math]

More frequently though, when we talk about the damped harmonic oscillator, we will discuss this force  :

[math]\displaystyle{ \vec{F} = -b\vec{v} }[/math]

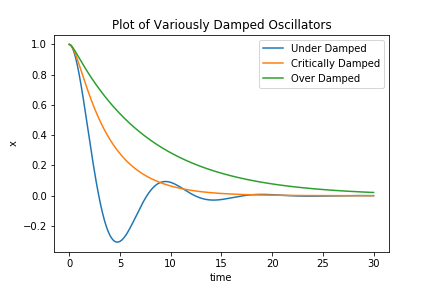
where b is the damping constant. The important difference between the two is that in the latter the force has a linear relationship to [math]\displaystyle{ \vec{v} }[/math]. There are three types of damping, depending on the coefficient, and they are labelled by how quickly the system damps out (reaches equilibrium). If the coefficient is small relative to the mass and spring constant, then the oscillator will be under damped, and still have some oscillatory behavior. If it is large relative to the mass and spring constant, the oscillator will be over damped, meaning that there will be no oscillations, but the system will take longer to arrive at an equilibrium because it has been slowed down by the dissipation. The fastest time of decay is when the system is critically damped, which occurs when [math]\displaystyle{ b^2 = 4mk }[/math]. The figure below illustrates these three possibilities, and is generated using the numpy based code from the Computational Methods section below.

Gravity

Introducing gravity to our model of spring mass systems is fairly straightforward (actually solving for it is somewhat more complicated, and we will only do so with computational methods described below). One simply adds the standard gravitational force [math]\displaystyle{ F = mg }[/math] to the force equations one has already. The most important point is to always remember which way is down: if your spring is hung upside down, then you may have chosen to define the origin at the equilibrium point and [math]\displaystyle{ +x }[/math] as being the downward direction, in which case you must take care to ensure that the sign of gravity corresponds.

A Computational Model

By definition, iterative prediction requires repeated calculations. This is extremely tedious to do by hand, so it is greatly preferable to perform them with a computer. Two programs are presented which perform these calculations.

An implementation of iterative motion for a spring system which feels gravitational force is provided in VPython here. The operative portion of the code is copied in the collapsible below (note, if one wishes to use this code, it will be necessary to include the proper import statements, which may be found at the link).

Expand

VPython Code

   ## constants and data
   g = 9.8
   mball = .5   ## mass of ball
   L0 = 0.3    ## relaxed length of spring
   ks = 50   ## spring constant (in N/m)
   deltat = .001  ## time step
   fscale = .07  ## scale factor for force arrow
   pscale = .4  ## scale factor for position arrow
   t = 0       ## initial time = 0 seconds
   ##########
   ## objects
   ceiling = box(pos=vec(0,0,0), size=vec(0.2,0.01,0.2)) ## origin is at ceiling
   ball = sphere(pos=vec(-.2637,-.1047,-.0429), radius=0.025, color=color.orange) ## note: spring initially compressed
   spring = helix(pos=ceiling.pos, color=color.cyan, thickness=.003, coils=40, radius=0.015)  ## create spring
   spring.axis = ball.pos - ceiling.pos  
   trail = curve(color=ball.color)  ## create trail of ball's position
   fnetarrow = arrow(pos = ball.pos, color = color.blue)  ## create arrow showing vector net force on ball
   parrow = arrow(pos = ball.pos, color = color.green)  ##create arrow showing vecotr momentum of ball
   ##########
   ## initial values
   ball.p = mball*vector  ## calculate initial momentum of ball
   #########
   ## improve the display
   scene.autoscale = 0             ## don't let camera zoom in and out as ball moves
   scene.center = vector(0,-L0,0)   ## move camera down to improve display visibility
   ##########
   ## calculation loop
   while t < 9.02:    ## sets end time for loop
       rate(300)
   ## calculate force on ball by spring
        l = ball.pos - ceiling.pos
        s = l.mag - L0
        lhat = l/l.mag
        fspring = ks * s * -lhat
   ## calculate net force on ball
        fnet = fspring + mball*vector(0, -g, 0)
        fnetarrow.pos = ball.pos
        fnetarrow.axis = fnet * fscale
   ## apply momentum principle
        ball.p = ball.p + fnet*deltat
        parrow.pos = ball.pos
        parrow.axis = ball.p * pscale
   ## update position
        ball.pos = ball.pos + (ball.p/mball)*deltat
   ## update axis of spring
        spring.axis = ball.pos - ceiling.pos
        trail.append(pos=ball.pos)
   ## update time   
        t = t + deltat
   ############
   ## Produce results
   print(ball.pos)
   print(ball.p/mball)

A second implementation using Numpy may be found here.

Examples

Simple Example

vertical spring-mass system

The simplest example of a spring mass system is one that moves in only one-direction.

Consider a massless spring of length 1.0 m with spring constant 40 N/m. If a 10 kg mass is released from rest while the spring is stretched downward to a length of 1.5 m, what is it's position after 0.2 seconds? The mass oscillates vertically, as shown to the right.

Expand

Solution

Step 1: Preliminaries It is first necessary to determine preliminaries. Since this is a one dimensional problem, no vectors are needed, but it is important to properly define our signs. Here we will assume the up is positive, so [math]\displaystyle{ F_g = mg }[/math] with [math]\displaystyle{ g = -9.8 m/s^2 }[/math]. Additionally, we must choose a time step: the time step used for each iteration must be small enough that we can assume a constant velocity over the interval, but not so large that solving the problem becomes incredibly time-consuming. It is appropriate in this situation to take [math]\displaystyle{ 0.1 s }[/math] as our time step.

Step 2: Calculating Initial Values Begin by calculating the object's initial momentum and the sum of the forces acting on it. The initial momentum is simply the product of the initial velocity, which is 0 m/s, as the object is released from rest. The forces acting on the mass are the gravitational force exerted by the Earth and the spring force. The net force may thus be calculated by summing these two forces.

[math]\displaystyle{ {\vec{p}_{i}} = {{m}\cdot\vec{v}_{i}} }[/math]

[math]\displaystyle{ {\vec{p}_{i}} = {{10kg}\cdot{0m/s}} = {0 Ns} }[/math]

[math]\displaystyle{ {\vec{F}_{grav}} = m\vec{g} }[/math]

[math]\displaystyle{ {\vec{F}_{grav}} = {10kg}\cdot(-9.8 m/s^2) = {-9.8 N} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {-kx} }[/math]

[math]\displaystyle{ {\vec{F}_{spring}} = {-40N/m}\cdot((-1.5 m)-(-1.0 m)) = {20 N} }[/math]

Note how the gravitational force is negative (downwards, as expected) and the spring force is positive (upwards, in opposition to gravity, as expected).

[math]\displaystyle{ {\vec{F}_{net}} = {\vec{F}_{grav} +{\vec{F}_{spring}}} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {-9.8N} +{20 N} = {10.2 N} }[/math]

Step 3: Update Momentum (Iteration 1)

Using the momentum update formula, calculate the momentum of the mass at the end of the given time step.

[math]\displaystyle{ \vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}\Delta t }[/math]

[math]\displaystyle{ {\vec{p}_{f} = {0Ns} + {10.2N}\cdot{0.1s} = {1.02Ns}} }[/math]

Step 4: Update Velocity (Iteration 1)

[math]\displaystyle{ {\vec{v}_{f} = \vec{v}_{i} + \frac{\vec{F}_{net}}{m}}\Delta t = \frac{\vec{p}_f}{m} }[/math]

[math]\displaystyle{ \vec{v}_{f} = \frac{1.02N}{1 kg} = {1.02m/s} }[/math]

Step 5: Update Position (Iteration 1)

Using the position update formula, calculate the position of the mass at the end of the given time step. For simplicity's sake, the average velocity used below is the velocity of the mass at the end of the time step. If we wished to increase our accuracy, we would average the initial and final velocities, and if we wished to increase it further we would use more advanced numerical methods (a brief description of which is provided in Fundamentals of Iterative Prediction with Varying Force. However, making this approximation is good enough for our purposes, and cuts down on arithmetic.

[math]\displaystyle{ \vec{r}_f = \vec{r}_i + \vec{v}_{avg} \Delta t }[/math]

[math]\displaystyle{ \vec{r}_{f} = -1.5m + (1.02m/s)\cdot(0.1s) = -1.398m }[/math]

Step 6: Update Time (Iteration 1)

[math]\displaystyle{ \vec{t}_f = \vec{t}_i + \Delta t }[/math]

[math]\displaystyle{ \vec{t}_f = 0s + 0.1s = 0.1s }[/math]

Step 7: Repeat Calculations

Repeat the above calculations using the "Iteration Round 1 Final Values" (calculated above) as the "Iteration Round 2 Initial Values".

Step 8: Update Forces (Iteration 2)

The gravitational force on the mass remains constant, and does not need to be recalculated.

[math]\displaystyle{ \vec{F}_{spring} = -kx }[/math]

[math]\displaystyle{ \vec{F}_{spring} = {-40N/m}\cdot((-1.398m)-(-1.0m)) = 15.92 N }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {\vec{F}_{grav} +{\vec{F}_{spring}}} }[/math]

[math]\displaystyle{ {\vec{F}_{net}} = {-9.8N} +{15.92 N} = {6.12N} }[/math]

Step 9: Update Momentum (Iteration 2)

[math]\displaystyle{ \vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}\Delta t }[/math]

[math]\displaystyle{ \vec{p}_{f} = 1.02Ns + (6.12N)\cdot(0.1s) = (1.632Ns) }[/math]

Step 10: Update Velocity (Iteration 2)

[math]\displaystyle{ \vec{v}_{f} = \vec{v}_{i} + \frac{\vec{F}_{net}}{m} \Delta t = \frac{\vec{p}}{m} }[/math]

[math]\displaystyle{ \vec{v}_{f} = \frac{1.632 N}{1 kg}= 1.632m/s }[/math]

Step 11: Update Position (Iteration 2)

[math]\displaystyle{ \vec{r}_{f} = \vec{r}_{i} + \vec{v}_{avg} \Delta t }[/math]

[math]\displaystyle{ \vec{r}_{f} = -1.398m + (1.632m/s)(0.1s) = -1.2348m }[/math]

Step 12: State Answer

After 0.2 seconds, the mass is at a position of 1.2348 m below the ceiling.

A Note on Iterations: While calculations can be performed manually, as above, it is advisable for more advanced problems that VPython or a similar program be used for such repetitive calculations in order to save time and reduce the likelihood of mathematical errors.

Middling Example

Now let us consider the above scenario and introduce a dissipative force of [math]\displaystyle{ \vec{F}_d = -b\vec{v} }[/math], and set [math]\displaystyle{ b = 1 kg/s }[/math]. What will be the position at a time of [math]\displaystyle{ 0.2 s }[/math] now?

Expand

Solution

We begin by recognizing that, presuming we use the same time steps, the first six steps stay exactly the same. Thus, if you have already done the simple level problem, we can perform only the second iteration. We will thus have initial conditions [math]\displaystyle{ x = -1.398 m }[/math] and [math]\displaystyle{ v = 1.02 m/s }[/math]. Now, let's compute the force, beginning with gravity:

[math]\displaystyle{ \vec{F}_g = m\vec{g} = (1 kg)\cdot(-9.8 m/s^2) = -9.8 N }[/math]

This naturally is unchanged. Next,

[math]\displaystyle{ \vec{F}_s = -(40 N/m)\cdot((-1.398 m)-(1.0 m)) = 15.92 N }[/math]

This too has stayed unchanged from the previous version of the problem, though one should note that for further iterations it will start to vary as well. Finally, we come to the difference:

[math]\displaystyle{ \vec{F}_d = -(1 kg/s)\cdot(1.02 m/s) = -1.02 N }[/math]

Note that here we are using the initial velocity to compute force. This is not strictly accurate, since the velocity is changing over the duration of the timestep, but since the final velocity depends on this force, it grows very complicated to account for this behavior, but achieving a more accurate answer with coarser time steps would require use of these techniques. We will not worry so much about this, however, and simply use this simplification. Thus we have our net force

[math]\displaystyle{ \vec{F}_{net} = -9.8 N + 15.92 N - 1.02 N = 5.1 N }[/math]

We now proceed as normal, computing

[math]\displaystyle{ \vec{p}_f = \vec{p}_i + \vec{F}_{net} \Delta t = 1.02 Ns + (5.1 N)(0.1 s) = 1.53 Ns }[/math]

[math]\displaystyle{ \vec{v}_f = \vec{v}_i + \frac{\vec{F}_{net}}{m} \Delta t = \frac{\vec{p}_f}{m} = 1.53 m/s }[/math]

[math]\displaystyle{ x_f = x_i + v \cdot \Delta t = -1.398 m + (1.53 m/s)(0.1 s) = -1.245 m }[/math]

This is, as expected, a shorter distance traveled than in the case without dissipation, since the system has been slowed down somewhat by the resistance.

Difficult Example

This problem will use a numerical simulation such as those described in the Computational Methods section. The notebook includes the code snippets to work this solution, though it is also helpful to investigate the process of writing one's own code.

We will consider the case of the driven oscillator from a strictly numerical point of view (if you wish to see a more thorough description of the problem, the Feynman Lectures sections 21-24 cover this entire topic in great detail). Consider a system with a mass of [math]\displaystyle{ 4 kg }[/math] attached to a spring with spring constant of [math]\displaystyle{ k = 100 N/m }[/math]. Assume that it is horizontal, such that gravity does not act upon it. Finally, introduce a force of the type [math]\displaystyle{ F = F_0 \cos(\omega_1 t) }[/math].

Now, consider a number of scenarios: note the behavior of the system, and describe in physical terms why this behavior occurs. Your thoughts should be guided by noticing key features such as the maximum amplitude, the time at which the maximum amplitude occurs, the rate at which amplitude changes, and whether there is any "wiggliness" that looks different from a normal oscillator.

1. Set [math]\displaystyle{ b = 0 }[/math], [math]\displaystyle{ F_0 = 1 }[/math], [math]\displaystyle{ x_0 = 0 }[/math], and [math]\displaystyle{ \omega_1 = 5 Hz }[/math]
2. Now, using the same parameters as above, set [math]\displaystyle{ x_0 = 1 }[/math]
3. Using the same parameters from (2), now set [math]\displaystyle{ b = 2 }[/math]
4. Using the same parameters from (3), set [math]\displaystyle{ F_0 = 2 }[/math]
5. Using the same parameters from (4), set [math]\displaystyle{ \omega_1 = 4 Hz }[/math]

Expand

Solution

1. We see that in this scenario, the amplitude is constantly increasing. When using a duration of [math]\displaystyle{ 30 s }[/math] and a time step of [math]\displaystyle{ 0.01 s }[/math] it reaches a maximum of approximately 2 on its last cycle. We see also, as expected, that it maintains the same frequency - the frequency of the driving force - for its duration, and starts from an initial position of 0. It should be noted, somewhat obviously, that were it not for the driving force this system wouldn't have done anything, in contrast to some of the systems we will investigate next.
2. Here we see again that the amplitude is constantly increasing. When using a duration of [math]\displaystyle{ 30 s }[/math] and a time step of [math]\displaystyle{ 0.01 s }[/math] it reaches a maximum of approximately 6 on its last cycle. It maintains the same frequency, a fact which is in fact due to intentional choice of parameters: if you haven't already, calculate the natural frequency [math]\displaystyle{ \omega_0 = \sqrt{k/m} }[/math], and you'll see that it is equal to [math]\displaystyle{ \omega_1 }[/math]. Therefore, since they started in phase, the driving force builds on the natural oscillation, and the amplitude grows substantially faster than in case (1).
3. Now that we have added a damping coefficient, we see something new happen: the system has two stages, one with decreasing amplitude, then one where it is essentially a harmonic oscillator. The first stage is known as the transient: essentially, the damping is bleeding off the initial conditions of the system, until we are left only with the balance between the damping and the forcing.
4. Here we see what we might naturally expect: the amplitude of the stable state has increased, and the duration of the transient has shortened, because the relative size of the initial conditions to the driving force has been decreased.
5. Finally, we look at what happens when the driving frequency is different from the natural frequency. We see that the amplitude of the stable state has in fact decreased. It turns out that we previously were at resonance, which for reasons we won't go into here (see the Feynman Lectures for more detail) was giving us much better response. This is a very important phenomenon, and you are likely to see it a lot in the future, especially if you are going into electrical engineering. We also can see that the transition from the transient to the stable state also has a period of wiggliness in the middle, where the oscillations from the initial frequency interfere with the oscillations from the driving frequency, before eventually the driving frequency takes over.

Connectedness

[A student should expand upon this section, following the Template]

While you may not need to precisely calculate the motion of spring-mass systems on a daily basis, understanding their behavior has led to the invention of many useful items. Among these are mattresses, clocks, and the suspension on cars.

However, the concept of iterative prediction applies to far more than masses on springs, as the concepts of physics apply far beyond textbook problems. By thinking in small enough time increments, the behavior of any system can be understood.

For example, in chemical engineering, entire processes can be broken down into simpler pieces and analyzed. These processes could then be modeled in order to predict future behavior.

History

The history of the spring mass system is essentially that of Hooke's law, as described in the article Simple Harmonic Motion, and repeated in part here. Thomas Hooke, an English scientist, discovered what is now known as Hooke's Law in 1660 while working on the springs of watches. A remarkable physicist, Hooke was also a pioneer in optics, astronomy, and fluid mechanics. He supported a theory of evolution nearly two hundred years before Darwin (although he did not know about the principle of natural selection), devised the inverse square law which Newton adapted, and accurately described air as individual particles separated by large distances. Solutions to the more complicated differential equations that describe the systems we looked at here are attributed to Leonhard Euler, Joseph Lagrange, and Jean D'Alembert, each a very influential mathematician .

See also

• Conservation of Momentum
• Predicting Change in multiple dimensions
• Impulse and Momentum
• Linear Momentum
• Momentum Principle
• Analytical Prediction
• Net Force
• Young's Modulus
• Tension
• Fundamentals of Iterative Prediction with Varying Force
• Simple Harmonic Motion
• Length and Stiffness of an Interatomic Bond

External links

• Interactive Spring-Mass Simulator
• The Feynman Lectures

Further Reading

• Matter and Interactions, 4th Edition

References