Gravitational Potential Energy: Difference between revisions

From Physics Book
Jump to navigation Jump to search
mNo edit summary
(Updated and fleshed out the main idea. Added Mathematical Model and Computational Model. Added A VPython link + various examples)
Line 1: Line 1:
'''Claimed by: Aidan Handa (Fall 2019)'''
'''Claimed by: Aidan Handa (Fall 2019)'''


==The Main Idea==
== Main Idea ==


Gravitational potential energy (U) is the energy stored in an object as a result of its position in a gravitational field and attractive forces from surrounding objects. Most commonly we see the potential energy for objects near the surface of Earth (U = mgh) to be equivalent to the work required to lift an object to a height h with no change in kinetic energy. Since force required to lift the object is weight (mg), the gravitation potential energy is weight times height.
Gravitational Potential Energy (<math>U_{grav}</math>) is the energy stored in an object as a result of its position in a gravitational field and attractive forces from surrounding objects. The general case of gravitational potential energy, when two objects with mass are attracted to each other, depends on the distance between the two and masses of each. The total gravitational energy <math>U_{grav}</math> is inversely proportional to the distance between the two objects with mass. In other words, the closer together together two things are, the greater the magnitude of gravitational potential energy <math>|U_{grav}|</math> will be. Additionally, the total gravitational potential energy <math>U_{grav}</math> is directly proportional to the masses of the objects. When the objects are more massive, the magnitude <math>|U_{grav}|</math> will be greater.


For a more general case, when two objects with mass are attracted to each other by gravity the gravitational potential depends on the distance between the two and masses of each. Kinetic energy is always positive and increases as an object approaches another. Thus, for total energy to be constant, gravitational potential energy must be less than or equal to 0. The gravity of one object does positive work as the other object approaches, which is why as distance r decreases the magnitude of U increases (becomes a larger negative value).  Additionally, the more mass objects have, the greater the potential energy.


===A Mathematical Model===


Gravitational Potential Energy Near Earth's Surface:
An important note is also that gravitational potential energy is negative. This results due to the integration determining gravitational potential energy but an intuitive way to understand this is that the negative sign indicates that when masses approach each other in a gravitational field gravity is doing positive work. If that didn't make sense, remember the idea that kinetic energy is always positive so when <math>K</math> increases if we want to keep <math>E_{total}</math> the same, <math>U_{grav}</math> must be negative.


<math>U = mgh\ </math>


* ''U'' is the gravitational potential energy in Joules (J)
* ''m'' is the mass of the object in kilograms (kg)
* ''g'' gravitational acceleration approximated at 9.8 N/kg
* ''h'' the distance the object is from Earth's surface in meters (m)


Gravitational Potential Energy Between Two Objects:
We commonly use gravitational potential energy when we're trying to determine the work required to life an object with mass <math>m</math> to a height a <math>h</math>. Since the gravitational potential energy for objects near the surface of the Earth (As we will derive in the Mathematical Model section) can be represented as <math>U_{grav} = mgh</math> we can intuitively see that the force due to gravity on an object of mass <math>m</math> would be <math>mg</math> and the height we'd be lifting it to would be <math>h</math>. Since work <math>W = \vec F \cdot \vec d</math> we see a parallel idea between <math>U_{grav}</math> and <math>W</math>.


<math>U = - G \frac{m_1 m_2}{r}\ </math>
* ''F'' is the gravitational potential energy
* ''G'' is the gravitational constant 6.67408×10<sup>-11</sup> m3⋅kg<sup>-1</sup>⋅s<sup>-2</sup>
* ''m''<sub>1</sub> is the first mass;
* ''m''<sub>2</sub> is the second mass;
* ''r'' is the distance between the centers of the masses
<br/>


[https://www.youtube.com/watch?v=zj5Th47UkC8]


===A Computational Model===
Checkout this [https://www.youtube.com/watch?v=z3ujg_CkslI video] for a quick review and explanation.


[http://www.physicsbook.gatech.edu/Energy_Graphs|Drawing Energy Graphs:]
* Draw U vs. r for the interaction
* At some r where you know K, plot the point (r,K)
* Add that value of K to the value U has at the same separation r
* Plot K+U at that r value, find a K when added to U at that r gives K+U
* Given these two points on the K graph, sketch K vs. r




=== Mathematical Model ===


[[File:Photo 2p.jpg|100px|thumb|left|Unbound System]] In figure 6.38 to the left, there is a representation of a spacecraft leaving the asteroid. The gravitational potential is negative because the interaction is attractive and by the graph we can see the potential increases with separation.


-----


===== General Form for Gravitational Potential Energy:  =====


<math>U_{grav} = -G\frac{m_1 m_2}{r}</math>




* <math>U_{grav}</math> is the total gravitational potential energy. Like other energy it is measured in Joules (<math>J</math>).
* <math>m_1</math> is the mass of the first object you are measuring <math>U_{grav}</math> between. The standard unit for mass is kilograms (<math>kg</math>).
* <math>m_2</math> is the mass of the second object you are measuring <math>U_{grav}</math> between. The standard unit for mass is kilograms (<math>kg</math>).
* <math>r</math> is the distance between the center of mass <math>cm</math> of both masses <math>m_1</math> and <math>m_2</math>. (If you don't know how to find center of mass yet, you can probably assume that its the center of whatever mass you're using). The standard unit for distance is meters (<math>m</math>).
* <math>G</math> is the gravitational constant or <math>6.67408 \times 10^-11 \frac{m^3}{kg \times s^2}</math>




[[File:Photo1phys.jpg|100px|thumb|right|Bound System]]  In the next figure to the right it is important to note as the asteroid gets farther away the kinetic energy will continue to fall and K approaches K+U, but K can not be negative since it involves velocity. When the two objects are far apart U is nearly 0 and K+U is nearly K. This graph is an example of a bound system, with the spacecraft having a smaller initial velocity headed away from the asteroid.
-----


We can make some simplifying approximations (similar to what we did with gravitational force) when we are trying to measure gravitational potential energy due to the Earth near the surface of the Earth.


===== Gravitational Potential Energy near the Earth's surface: =====


<math>U_{grav} = mgh</math>




* <math>U_{grav}</math> is the total gravitational potential energy. Like other energy it is measured in Joules (<math>J</math>).
* <math>m</math> is the mass of the object you are measuring <math>U_{grav}</math> of. The standard unit for mass is kilograms (<math>kg</math>).
* <math>h</math> is the height above the Earth's surface that the object is (make sure that it is near the Earth's surface. A good rule of thumb is that it really shouldn't be in space :-) ). The standard unit for height is meters (<math>m</math>).




-----


VPython:


Kinetic and potential energies as a function of time for the system of a spacecraft and the Earth (including the influence of the Moon)


''To create the graphs''
=== Computational Model ===


trail = curve(color=craft.color)# This creates a trail for the spacecraft
In order to understand gravitational potential energy in a computational manner, we must be able to represent it in some way which we can visually understand it. To do this, we will use an energy graph. An ''energy graph'' is a graph which plots potential energy, kinetic energy, and total energy. There are a few easy steps to follow when making an energy graph.
U_graph = gcurve(color=color.blue) #A plot of the Potential energy
K_graph = gcurve(color=color.yellow) #A plot of the Kinetic energy
Energy_graph = gcurve(color=color.green) #A plot of the Total energy


''To calculate energies''
# Draw <math>U_{grav}</math> vs <math>|\vec r|</math> for the interaction (<math>|\vec r|</math> is the distance the object is from what it's attracted to)
# At some distance <math>|\vec r|</math> where <math>K</math> is known, plot the point <math>(|\vec r|, K)</math>
# Add the known value of <math>K</math> to the value of <math>U</math> at that same separation <math>|\vec r|</math>
# Plot the horizontal line <math>K+U</math> across the graph
# Calculate the rest of <math>K</math> knowing that <math>K+U</math> = the same constant
# Plot the values


K_craft = 0.5*mcraft*(mag(pcraft/mcraft))**2
U_craft_Earth = -G*mcraft*mEarth/mag(craft.pos-Earth.pos) #Craft + Earth interaction energy
U_craft_Moon = -G*mcraft*mMoon/mag(craft.pos-moon.pos) #Craft + Moon interaction energy
E = K_craft + U_craft_Earth + U_craft_Moon #Approximate Total energy


''Graph energies as a function of time''


U_graph.plot(pos=(t,U_craft_Earth+U_craft_Moon)) #Potential energy as a function of time
[[File:Totalenergy.gif|frame|none|alt=|caption ]]
K_graph.plot(pos=(t,K_craft)) #Kinetic energy as a function of time
 
Energy_graph.plot(pos=(t,E)) #Total energy as a function of time
 
 
The above graph shows an example of what an energy versus distance graph may look like. We can see that as the distance increases, <math>U_{grav}</math> decreases and <math>K</math> increases.
 
 
 
==== VPython Examples ====
 
 
 
Suppose that we have a spaceship that is passing close to the Earth. We can computationally model the gravitational potential energy of this spaceship and visually represent it using energy graphs. The basic structure of our program will follow what is usually done for VPython programs:
 
<pre class="pseudocode">Pick a delta t
Initialize our variables
while our time &lt; time bound do
Calculate new values for our variables
Update how they are presented
increment our time + delta t</pre>
 
 
 
 
''Create/Initialize the Energy Graphs''
 
<pre class="pseudocode">trail = curve(color=craft.color) #This creates a trail for the spacecraft
U_graph = gcurve(color=color.blue) #A plot of the Potential energy
K_graph = gcurve(color=color.yellow) #A plot of the Kinetic energy
Energy_graph = gcurve(color=color.green)#A plot of the Total energy</pre>
''Calculate and Update the variables in our Loop''
 
<pre class="pseudocode">K_craft = 0.5*mcraft*mag2(pcraft/mcraft) #Kinetic Energy using equation: .5mv^2
U_craft_Earth = -G*mcraft*mEarth/mag(craft.pos-Earth.pos) #Craft + Earth interaction energy
E = K_craft + U_craft_Earth #Approximate Total energy</pre>
''Update our graphs''
 
<pre class="pseudocode">U_graph.plot(pos=(t,U_craft_Earth)) #Potential energy as a function of time
K_graph.plot(pos=(t,K_craft)) #Kinetic energy as a function of time
Energy_graph.plot(pos=(t,E)) #Total energy as a function of time</pre>
 
 
 
 
Here is what a slightly more complex product would like like (this example has the moon's gravity incident on the spaceship as well):
 
Click [https://trinket.io/embed/glowscript/370440404c?outputOnly=true here] to see it in action if you can't see it below.
 


==Examples==
==Examples==

Revision as of 01:39, 18 November 2019

Claimed by: Aidan Handa (Fall 2019)

Main Idea

Gravitational Potential Energy ([math]\displaystyle{ U_{grav} }[/math]) is the energy stored in an object as a result of its position in a gravitational field and attractive forces from surrounding objects. The general case of gravitational potential energy, when two objects with mass are attracted to each other, depends on the distance between the two and masses of each. The total gravitational energy [math]\displaystyle{ U_{grav} }[/math] is inversely proportional to the distance between the two objects with mass. In other words, the closer together together two things are, the greater the magnitude of gravitational potential energy [math]\displaystyle{ |U_{grav}| }[/math] will be. Additionally, the total gravitational potential energy [math]\displaystyle{ U_{grav} }[/math] is directly proportional to the masses of the objects. When the objects are more massive, the magnitude [math]\displaystyle{ |U_{grav}| }[/math] will be greater.


An important note is also that gravitational potential energy is negative. This results due to the integration determining gravitational potential energy but an intuitive way to understand this is that the negative sign indicates that when masses approach each other in a gravitational field gravity is doing positive work. If that didn't make sense, remember the idea that kinetic energy is always positive so when [math]\displaystyle{ K }[/math] increases if we want to keep [math]\displaystyle{ E_{total} }[/math] the same, [math]\displaystyle{ U_{grav} }[/math] must be negative.


We commonly use gravitational potential energy when we're trying to determine the work required to life an object with mass [math]\displaystyle{ m }[/math] to a height a [math]\displaystyle{ h }[/math]. Since the gravitational potential energy for objects near the surface of the Earth (As we will derive in the Mathematical Model section) can be represented as [math]\displaystyle{ U_{grav} = mgh }[/math] we can intuitively see that the force due to gravity on an object of mass [math]\displaystyle{ m }[/math] would be [math]\displaystyle{ mg }[/math] and the height we'd be lifting it to would be [math]\displaystyle{ h }[/math]. Since work [math]\displaystyle{ W = \vec F \cdot \vec d }[/math] we see a parallel idea between [math]\displaystyle{ U_{grav} }[/math] and [math]\displaystyle{ W }[/math].


Checkout this video for a quick review and explanation.


Mathematical Model

General Form for Gravitational Potential Energy:

[math]\displaystyle{ U_{grav} = -G\frac{m_1 m_2}{r} }[/math]


  • [math]\displaystyle{ U_{grav} }[/math] is the total gravitational potential energy. Like other energy it is measured in Joules ([math]\displaystyle{ J }[/math]).
  • [math]\displaystyle{ m_1 }[/math] is the mass of the first object you are measuring [math]\displaystyle{ U_{grav} }[/math] between. The standard unit for mass is kilograms ([math]\displaystyle{ kg }[/math]).
  • [math]\displaystyle{ m_2 }[/math] is the mass of the second object you are measuring [math]\displaystyle{ U_{grav} }[/math] between. The standard unit for mass is kilograms ([math]\displaystyle{ kg }[/math]).
  • [math]\displaystyle{ r }[/math] is the distance between the center of mass [math]\displaystyle{ cm }[/math] of both masses [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math]. (If you don't know how to find center of mass yet, you can probably assume that its the center of whatever mass you're using). The standard unit for distance is meters ([math]\displaystyle{ m }[/math]).
  • [math]\displaystyle{ G }[/math] is the gravitational constant or [math]\displaystyle{ 6.67408 \times 10^-11 \frac{m^3}{kg \times s^2} }[/math]


We can make some simplifying approximations (similar to what we did with gravitational force) when we are trying to measure gravitational potential energy due to the Earth near the surface of the Earth.

Gravitational Potential Energy near the Earth's surface:

[math]\displaystyle{ U_{grav} = mgh }[/math]


  • [math]\displaystyle{ U_{grav} }[/math] is the total gravitational potential energy. Like other energy it is measured in Joules ([math]\displaystyle{ J }[/math]).
  • [math]\displaystyle{ m }[/math] is the mass of the object you are measuring [math]\displaystyle{ U_{grav} }[/math] of. The standard unit for mass is kilograms ([math]\displaystyle{ kg }[/math]).
  • [math]\displaystyle{ h }[/math] is the height above the Earth's surface that the object is (make sure that it is near the Earth's surface. A good rule of thumb is that it really shouldn't be in space :-) ). The standard unit for height is meters ([math]\displaystyle{ m }[/math]).



Computational Model

In order to understand gravitational potential energy in a computational manner, we must be able to represent it in some way which we can visually understand it. To do this, we will use an energy graph. An energy graph is a graph which plots potential energy, kinetic energy, and total energy. There are a few easy steps to follow when making an energy graph.

  1. Draw [math]\displaystyle{ U_{grav} }[/math] vs [math]\displaystyle{ |\vec r| }[/math] for the interaction ([math]\displaystyle{ |\vec r| }[/math] is the distance the object is from what it's attracted to)
  2. At some distance [math]\displaystyle{ |\vec r| }[/math] where [math]\displaystyle{ K }[/math] is known, plot the point [math]\displaystyle{ (|\vec r|, K) }[/math]
  3. Add the known value of [math]\displaystyle{ K }[/math] to the value of [math]\displaystyle{ U }[/math] at that same separation [math]\displaystyle{ |\vec r| }[/math]
  4. Plot the horizontal line [math]\displaystyle{ K+U }[/math] across the graph
  5. Calculate the rest of [math]\displaystyle{ K }[/math] knowing that [math]\displaystyle{ K+U }[/math] = the same constant
  6. Plot the values


caption


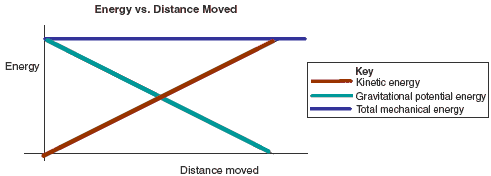
The above graph shows an example of what an energy versus distance graph may look like. We can see that as the distance increases, [math]\displaystyle{ U_{grav} }[/math] decreases and [math]\displaystyle{ K }[/math] increases.


VPython Examples

Suppose that we have a spaceship that is passing close to the Earth. We can computationally model the gravitational potential energy of this spaceship and visually represent it using energy graphs. The basic structure of our program will follow what is usually done for VPython programs: 

Pick a delta t
Initialize our variables
while our time < time bound do
	Calculate new values for our variables
	Update how they are presented
	increment our time + delta t



Create/Initialize the Energy Graphs 

trail = curve(color=craft.color)		#This creates a trail for the spacecraft
U_graph = gcurve(color=color.blue) 		#A plot of the Potential energy
K_graph = gcurve(color=color.yellow) 	#A plot of the Kinetic energy
Energy_graph = gcurve(color=color.green)#A plot of the Total energy

Calculate and Update the variables in our Loop 

K_craft = 0.5*mcraft*mag2(pcraft/mcraft)	#Kinetic Energy using equation: .5mv^2
U_craft_Earth = -G*mcraft*mEarth/mag(craft.pos-Earth.pos) #Craft + Earth interaction energy
E = K_craft + U_craft_Earth		#Approximate Total energy

Update our graphs 

U_graph.plot(pos=(t,U_craft_Earth))		#Potential energy as a function of time
K_graph.plot(pos=(t,K_craft))			#Kinetic energy as a function of time
Energy_graph.plot(pos=(t,E))			#Total energy as a function of time



Here is what a slightly more complex product would like like (this example has the moon's gravity incident on the spaceship as well):

Click here to see it in action if you can't see it below.


Examples

Simple

Question

Gravity field near earth at 1,2 and A.

A ball of mass 100 grams is 7m above the ground, initially at rest (Ki=0). When the ball is 4 m above the ground what is the final kinetic energy? Choose the ball + Earth system. First look at the two pictures to the right in order to see the ball + Earth as a system and to see what equations to use. The rest energy is 0.

Solution

[math]\displaystyle{ 0=\Delta K_{(Earth)} + \Delta K_{(ball)} +\Delta U }[/math],
[math]\displaystyle{ 0= 0+(K_{(ball,f)} -0)+ \Delta(mgy) }[/math]
[math]\displaystyle{ 0= K_{(ball,f)} + (0.1 kg)*(9.8 N/M)*(-3 m) }[/math]
[math]\displaystyle{ U_g -2.94J }[/math]

This is used to solve for kinetic energy

[math]\displaystyle{ K_{(ball,f)} = 2.94 J }[/math]
Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Ball+Earth system

Middling

Question

In February 2013 a large meteor, whose mass has been estimated to be 1.2x107 kg, fell to Earth near Chelyabinsk, Russia. (This meteor exploded spectacularly at height of about 30 km, doing significant damage to objects on the ground.) Consider a meteor of the same mass falling toward the Earth. Choose the Earth plus the meteor as the system. As the meteor falls from a distance of 1e8 m from the center of the Earth to 1e7 m, what is the change n the kinetic energy of the meteor? Explain the signs of the changes in kinetic and potential energy of the system.

Solution

The meteor in question mushroom cloud's cap.
[math]\displaystyle{ U_{(grav)} }[/math] must first be calculated explicitly for each state
[math]\displaystyle{ U_i = G \frac{m_E m_m}{r^2} = -6.7e-11 Nm^2/kg^2 \frac{6e24 kg * 1.2e7 kg m_m}{1e8^2m} }[/math]
[math]\displaystyle{ = -4.82e13J }[/math]
[math]\displaystyle{ U_f = G \frac{m_E m_m}{r^2}= -6.7e-11 Nm^2/kg^2 \frac{6e24 kg * 1.2e7 kg m_m}{1e7^2m} }[/math]
[math]\displaystyle{ = -4.82e14J }[/math]

Both the initial and final values are negative. Separation decreases so we know that the final potential energy minus the initial is greater than 0. Apply the Energy Principle now to find the final answer.


[math]\displaystyle{ \Delta K_{(meteor)}+(-4.82e14 J - -4.82e13J)=0 }[/math]
[math]\displaystyle{ \Delta K_{(meteor)}=4.34e14J }[/math]

Difficult

Question

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127
Robot Spacecraft blastoff

A robot spacecraft lands on an asteroid, picks up a sample, and blasts off to return to the Earth; it's total mass is 1500 kg. When it is 200 km from the center of mass of the asteroid, its speed is 5.0 m/s, and the rockets are turned off. At the moment when it has coasted to a distance 500 km from the center of the asteroid, its speed has a decreased to 4.1 m/s. Calculate the mass of the asteroid.

Solution

M will be the mass of the asteroid and m will be the mass of the spacecraft.

[math]\displaystyle{ E_{(f)}= E_i + W }[/math]

Mc^2 + K_Mf+ mc^2 + [math]\displaystyle{ K_{(mf)}+ U_{(f)} }[/math]= Mc^2 + K_Mf+ mc^2 + [math]\displaystyle{ K_{(m,i)}+ U_{(i)} + W }[/math]

[math]\displaystyle{ K_{(m,f)}+ U_{(f)}= K_{(m,i)}+ U_{(i)} + 0 }[/math]
[math]\displaystyle{ .5 m v_{(f)}^2 - G \frac{M m}{r_{(f)}}= .5 m v_{(i)}^2 - G \frac{M m}{r_{(i)}} }[/math]

Can factor out the m

[math]\displaystyle{ m (.5 v_{(f)}^2 - G \frac{M }{r_{(f)}})= m(.5 v_{(i)}^2 - G \frac{M }{r_{(i)}} ) }[/math]
[math]\displaystyle{ GM (\frac{1 }{r_{(i)}} -\frac{1 }{r_{(f)}} )= .5 (v_{(i)}^2 -v_{(f)}^2) }[/math]

Connectedness

Gravitational potential energy can be related to industrial engineering for someone who chooses to work in a manufacturing or aerospace. It is also very important to include when determining the escape velocity and other forces necessary for rockets, probes, and satellites to travel within space.

History

Galileo Galilei and Isaac Newton discovered how forces are related to acceleration. Newton summed up this information with his Laws of Motion. Mechanical energy was discovered by analyzing the equations derived from Newton's Laws. It was later realized that when two objects interact they exert forces on each other and that work (W=Fd) must be replaced with potential energy in a system of interacting objects within a gravitational field.

See also

Might be interesting to explore spring potential!

http://theory.uwinnipeg.ca/physics/work/node5.html

Further reading

Books, articles, or other print media on this topic:

https://books.google.com/books?id=8p0gaOL802AC&pg=PA123&dq=physics+gravitational+potential&hl=en&sa=X&ved=0CB0Q6AEwAGoVChMIkKHT0NadyQIVBtgeCh2y8Qrm#v=onepage&q=physics%20gravitational%20potential&f=false

External links

Internet resources on this topic:

Simple Explanation:

http://scienceworld.wolfram.com/physics/GravitationalForce.html

Videos:

https://www.youtube.com/watch?v=a91DAsbYCo4

https://www.youtube.com/watch?v=8a4D2xqHBF4

References

http://www.physicsclassroom.com/class/circles/Lesson-3/Newton-s-Law-of-Universal-Gravitation

http://matterandinteractions.org/

http://www.physicsclassroom.com/class/energy/Lesson-1/Potential-Energy

http://hyperphysics.phy-astr.gsu.edu/hbase/gpot.html

http://weelookang.blogspot.com/2010/10/ejs-open-source-gravity-field-model.html

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Gravitational_Potential_Energy&oldid=38050"