Angular Resolution
The Main Idea
Angular Resolution is the ability of a device to visibly separate two different objects in space that are located a close angular distance to each other. The closer the objects are while the device can still see distinguish between them, the higher the angular resolution is.
Angular resolution is also referred to as spatial resolution.
A Mathematical Model
The equation for angular resolution is [math]\displaystyle{ {∆θ = \frac{λ}{W}} }[/math] where W is the width of the device
A Computational Model
The top most image demonstrates the highest angular resolution. It is most able to differentiate between the two objects. The bottom image demonstrates the lowest angular resolution. It is unable to differentiate between the two objects.
Summary of Derivation
The maximum for angular momentum is the spot at which it is the brightest. The mimumum is the spot at which it is the darkest. The maximum is at angle θ while the minimum is at angle (θ + ∆θ). A minimum can only occur if light is passing through the first slit and the middle slit of width of the device. This results in a path difference of [math]\displaystyle{ {\frac{Nλ}{2}} }[/math] for the maximum [math]\displaystyle{ {\frac{Nλ}{2} + \frac{λ}{2}} }[/math] for the minimum. Through a series of trig identities, is was discovered that the angular half width of a maximum is [math]\displaystyle{ {∆θ = \frac{λ}{W}} }[/math]. This result is the definition of angular resolution.
Examples and Applications
Simple
The main application for angular resolution is in telescopes. The ability to clearly see objects in space through a telescope is mostly determined by angular resolution. The higher the resolution, the better the clarity and detail of the images.
Find the angular resolution in radians for a telescope with a diameter of 9 meters. Consider the case of red light (700 nanometers).
[math]\displaystyle{ {θ = \frac{λ}{W}} }[/math]
[math]\displaystyle{ {θ = \frac{500x10e-9m}{9m}} }[/math]
[math]\displaystyle{ {θ = 5.55e-8 radians} }[/math]
Difficult
Another application for angular resolution is the human eye. An indication of good angular resolution is seeing crisp, clear images.
The human eye has a pupil diameter of 3mm during the day and an average optical sensitivity of 0.55um. Find the angular resolution of the average human eye during the day in degrees.
[math]\displaystyle{ {θ = \frac{λ}{W}} }[/math]
[math]\displaystyle{ {θ = \frac{0.55um}{3} } }[/math]
Now we must convert units and change into degrees.
[math]\displaystyle{ {θ = \frac{0.55um}{3} x \frac{180 degrees}{π} x \frac{1mm}{1000um}} }[/math]
[math]\displaystyle{ {θ = 0.0128 degrees} }[/math]
Connectedness
How is this topic connected to something that you are interested in? This topic directly relates to space exploration. The ability to increase telescope angular resolution is directly linked to the ability to discover new planets and explore ones we are currently aware of.
How is it connected to your major? I am an industrial engineering major with a concentration in optimization. Optimizing angular resolution is the best way to optimize a telescope for visibility, clarity, and detail of image capabilities.
Is there an interesting industrial application? This concept can be applied to any product that is seen through. This can be applied to eye sight such as surgery, contacts, and glasses. It can also be applied to telescopes, magnify glasses, and other sight enhancing equipment.
History

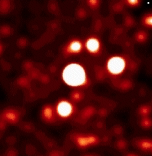

Angular resolution has had a significant role in the "Space Race" and is used currently to keep improve telescopes. The better the angular resolution, the better the images from telescopes. The images that have recently been taken of pluto showing possible water supplies would not have been possible without the insanely high angular resolution of the telescope that was used. These three images demonstrate the drastic improvements that have been made over the last 25 years in regards to the angular resolution of telescopes.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Matter and Interactions 3rd Edition
External links
References
https://www.astro.umd.edu/~thuard/astr288c/lecture6-notes.pdf
http://coolcosmos.ipac.caltech.edu/cosmic_classroom/cosmic_reference/resolution.html
http://www.spitzer.caltech.edu
http://landsat.gsfc.nasa.gov/wp-content/uploads/2013/06/RS_45.pdf
