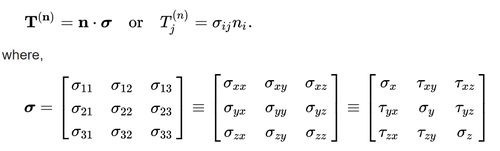Fluid Mechanics

Edited by Abieshek Subramaniam Fall 2018

The Main Idea

Fluid mechanics focuses on how fluids (gases or liquids) respond to forces that finds its importance in various fields, specifically hydraulics and many engineering disciplines. (1,2) Water has been historically studied the most out of most fluids, but the field is not limited to water. (1) The field of fluid dynamics consists of: fluid statics, fluid kinematics, and fluid dynamics. Fluid statics is the study of fluids at rest, fluid kinematics is the study of fluids when they are moving (does not include pressure forces), and fluid dynamics is the study of fluids when they are moving while incorporating pressure forces.

Mathematical Model

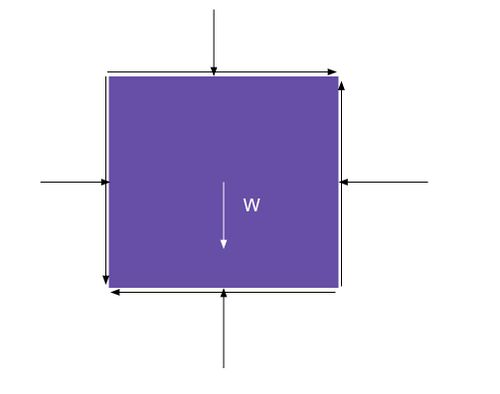
While very complex, many physics principles are applicable to fluid mechanics, namely Newton’s first and second law. Fluid statics utilizes Newton’s first law, an object at rest will stay at rest unless acted upon by an unbalanced force, or Fnet = 0. (4) Fluid mechanics and Fluid dynamics use Newton’s second law which deals with the behavior of objects where existing forces are unbalanced, or Fnet = mass x acceleration. This first picture represents a fluid particle at rest and the second represents a fluid particle in motion.

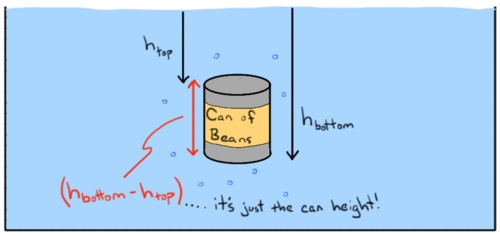
Fluid mechanics also explores the buoyancy of objects in the water and the tendency of motion of the object based on the force from gravity and the water. This force due to buoyancy that often opposes gravity, is due to a difference in pressure between the bottom and top of a submerged object. The pressure increases as you go down the water and thus the buoyant force is created by the fact that the bottom of an object is always deeper than the top of the object so the upward force must be greater than the downward force resulting in this buoyant force from the water as shown in the image below. In fact, the buoyant force can be described as the difference between the upward and downward force (17).

Another key thing to note is that even if the same object as shown in the above image is submerged deeper and deeper, the buoyant force will remain the same. This may seem counterintuitive as pressure increases the deep your go, however, it is important to remember that the buoyant force is based on the difference in pressure of the top and the bottom of the object and thus since the entire object is moving deeper, the difference would not change resulting in the same buoyant force (17).

Computational Model

There is an entire branch of fluid mechanics that is dedicated to computationally modeling fluid dynamics using numerical analysis and data structures. (6) While extremely complex, here are some pictures that have been modeled using computational fluid dynamics.

Examples: A sampling of equations that could be used in an introductory fluid mechanics class.

Navier-Stokes equations describe the motion of viscous fluid substances. It is derived as a form of the cauchy momentum equation. (7)

ρ is the density
u is the flow velocity
∇∙ is the divergence (8) (the volume density of the outward magnitude and direction of a flow (flux)) (9)
p is the pressure
t is time
I is the identity matrix
τ is the deviatoric stress tensor
g represents body accelerations acting on the continuum
⊗ is the outer product that makes the equation u⊗v = uvT true

Reynolds number flows is used to predict flow patterns. (11) The equation is:

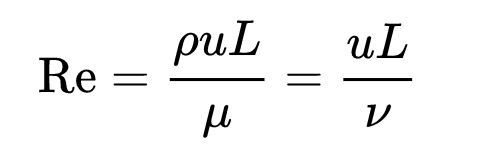
ρ is the density of the fluid (SI units: kg/m3)
u is the velocity of the fluid with respect to the object (m/s)
L is a characteristic linear dimension (defines the length scale of a physical system) (12.) (m)
μ is the dynamic viscosity of the fluid (Pa·s or N·s/m2 or kg/m·s)
ν is the kinematic viscosity of the fluid (m2/s).

The Bernoulli Equation is the equation that is used to show that energy is conserved when analyzing fluids. There is a term called the “Bernoulli effect” that is whe fluid pressure lowers in regions where flow velocity has gone up. (13) The basis of the equation is:

energy/unit initial = energy/unit final
- P1 + ½ ρv12 + ρgh1 = P2 + ½ ρv22 + ρgh2
  - P is the pressure energy

The Archimedes Principle uses P V and g to determine the buoyant force for an object.

Fbouyant = pVfg
- When rearranged and using substitution we get Fbouyant = Wf
  - This tells us that the buoyant force is equal to the weight of the fluid displaced by the object.
    - It is important to note that the density (p) in this case is the density of the fluid and not the object that is being submerged.

Example Questions

A cube, whom you have developed a strong companionship with, has a total mass of 2.33kg. What must be the minimum side length of the cube so that it floats in sea water of density 1025 kg/m^3?

Based on the Archimedes principle we know that the Wcube = Fbuoyancy.
We also know that the weight of an object is the mass times the gravity and we know that Fbouyancy is = PVfg based on Archimedes principle
- Thus mg = pVfg
  - V = L^3 where L is the length of the cube
    - mg = PL^3g
      - Simplified L = (m/p)^1/3
        L = (2.33/1025)^1/3 = .131m

A huge spherical helium filled balloon painted to look like a cow is prevented from floating upward by a rope tying it to the ground. The balloon plastic structure plus all the helium gas inside of the balloon has a total mass of 9.20kg. The diameter of the balloon is 3.50m. The density of the air is 1.23 kg/m^3. What is the tension in the rope?

This question requires the use of Archimedes principle and an understanding of all of the forces that are present in the system.
Fb = W + Tension
- In this question you can assume that the liquid is air and find the buoyancy force produced by air. Thus we can set the force upwards (buoyancy) equal to the force downwards (weight plus the tension) because we know there is no net force.
  - Next by using Archimedes principle we can solve for the force of tension with known variables : FT = pVg - mg
  - FT = 1.23(4/3)(pi)(3.5/2)^3(g) - 9.2(g) = 180 N

Connectedness

How is the topic connected to something that I am interested in?
- This topic is very interesting because it has real applications with the human body. The human body is nearly 60% water so fluid mechanics comes into play with other subjects such as biology and together the two fields of study can help with the research involved to fight diseases and save lives. (3)
How is it connected to my major?
- My major is Industrial Engineering, and while on the surface fluid mechanics has no direct connection to IE, IE is very focused on efficiency and optimization. These two characteristics of IE are primary goals of people who study fluid dynamics: optimizing the use of fluids in the most efficient way possible.
Is there an interesting industrial application?
- Fluid mechanics is extremely applicable in industries that incorporate hydraulics and hydroelectric power. Both of these, and many other industrial applications, play a huge part in various mechanisms used in daily life.
- Georgia Tech also has its own fluid mechanics lab!

History

The emergence of fluid mechanics as an interest began in around 250 BC when it was founded by Archimedes, a famous mathematician and inventor. Allegedly, Archimedes was taking a bath when suddenly he jumped out of the bath and ran through the streets of Syracuse, Greece screaming “Eureka!” Hydrodynamics was not deeply studied until the 18th century when Leonhard Euler and Daniel Bernoulli explored hydrodynamics, which was more based off of Newton’s dynamic principles. (1.)

References

The references are numbered according to the numbers in parenthesis throughout the page.

1. [1] 2. [2] 3. Pocock, Jennifer. ASEE Prism; Washington Vol. 26, Iss. 2, (Oct 2016): 22. “Fluid Dynamic” 4. [3] 5. [4] 6. [5] 7. [6] 8. [7] 9. [8] 10. [9] 11. [10] 12. [11] 13. [12] 14. [13] 15. [14] 16. [15] 17. [16]