Hooke’s Law

Author: Vinutna Veeragandham

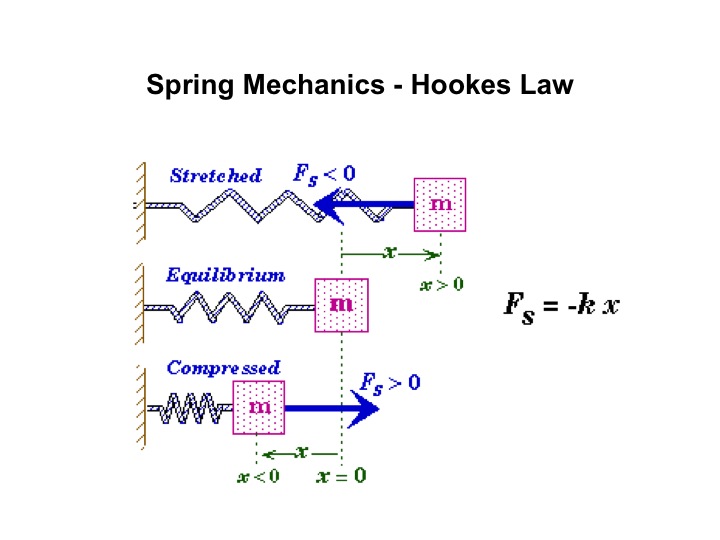
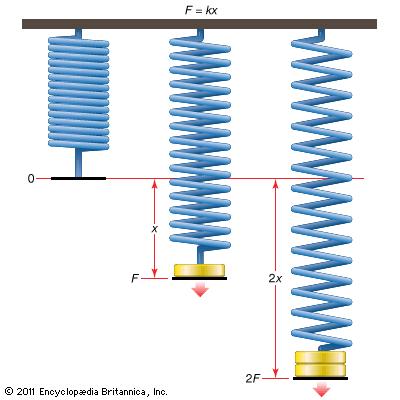
Hooke's Law: the force needed to extend or compress a spring by some distance is proportional to that distance.

The Main Idea

Hooke's Law demonstrates the relationship between forces applied to a spring and elasticity. It states that the force needed to extend or compress a spring by some distance is proportional to that distance. This law applies to many different materials such as balloons or strings; an elastic body to which Hooke's law applies is known as linear-elastic. Hooke's Law has been the basis for the modern Theory of Elasticity, led to creation of new inventions as well as been the foundation of many different branches of science such as seismology, molecular mechanics and acoustics.

A Mathematical Model

   F = -kX

F - restoring force, force by which the free end of the spring is being pulled, SI Units: Newtons

k - spring constant, an inherent property of the string, SI Units: Meters

X - spring displacement from the spring's free end while at equilibrium position, SI Units: Newtons/Meters

A Computational Model

A computational representation of Hooke's Law can be created using VPython. The code below puts Hooke's law in action.

  # GlowScript 1.1 VPython
   
   L0=.1 #the natural length of the spring
   k=15 #spring constant
   
  #the holder is the top plate for the spring
   holder= box(pos=vec(-.1,.1,0), size=vec(.1,.005,.1))
   
  #the ball and the spring should be obvious 
   
  #note that the ball has a trail
   ball=sphere(pos=vec(-.1,-L0+.1,0), radius=0.02, color=color.red, make_trail=true)
   spring=helix(pos=holder.pos, axis=ball.pos-holder.pos, radius=.02, coils=10)
   ball.m=0.1 #mass of the ball in kg
   ball.p=ball.m*vec(0,0,0) #starting momentum mass times velocity
   dr=vec(0,-0.05,0) #this is the displacement of the spring
   ball.pos=ball.pos+dr
   g=vec(0,-9.8,0) #gravitational field
   t=0
   dt=0.01 #size of the time step
   
  #putting the loop as "while True" means it runs forever
   
  #you could change this to while t< 10: or something 
   while t<3: 
   rate(100) #this says 100 calculations per second
   
  #L is the length of the spring, from the holder to the ball
   L=ball.pos-holder.pos
   
  #remember that mag(R) gives the magnitude of vector R
   
  #remember that norm(R) gives the unit vector for R
   Fs=-k*(mag(L)-L0)*norm(L) #this is Hooke's law
   
  #this calculates the net force
   F=Fs+ball.m*g
   
  #update the momentum
   ball.p=ball.p+F*dt
   
  #update the position of the ball
   ball.pos= ball.pos +ball.p*dt/ball.m
   
  #this next line updates the spring
   spring.axis=ball.pos-holder.pos

Examples

Simple

A spring has a spring constant that is equal to 3.5. What force will make it stretch 4 cm?

 F = k * x
 F = 3.5 * 4
 F = 14 kg

Middling

A 0.15 kg mass is attached to a vertical spring and hangs at rest a distance of 4.6 cm below its original position. An additional 0.50 Kg mass is then suspended from the first mass and the system is allowed to descend to a new equilibrium position. What is the total extension of the spring?

  m = 0.15 kg
  M = 0.5 kg
  x = 4.6 cm
  X = total stretch distance
  F = applied force
  
  Find X...
  
  X = F/k
  F = kx = mg
  k = mg/x
  k = [ (0.15) * (9.8) ] / 0.046
  k =  32 N/m
  
  With both masses...
  
  X = [ (m + M) * g ] / k
  X = [ (0.15 + 0.50) * (9.8) ] / 32
  X = 0.20 m

Difficult

A mass of 1.0kg is attached to a spring obeying Hooke's Law F = k*s, where F is the force applied and s the spring extension. The spring constant, k is 50 N/m. The spring and the object lie on a surface tilted 45 degrees with respect to the vertical. Neglect friction. Answer the following questions:

a. What is the extension of the spring?

b. What is the work done by gravity in extending the spring by the above extension?

  a)  
  
  1kg = 9.8 N
   
  Resolve the force into horizontal component...   
  9.8 * sin(45) = 6.93
  
  F = k*s --> F/k = s
  
  s = 6.93/50 = 0.139 m

  b)
  
  Work done by gravity can be calculated by calculating the change in potential energy.
  
  U = (1/2) * k * (x^2)
  = (1/2) * 50 * (0.139^2) 
  = 0.483 J

Connectedness

Hooke's law is relevant in our everyday lives from small objects all the way to massive structures. We can see the simplest of applications of Hooke's law in rubber bands, scrunchies and even our clothes. Just as Hooke's law prescribes we can see that there is a limit to which they can be stretched and still restore their original shape; after this limit, they will break or lose their shape. Larger applications of Hooke's law can be seen in the newer constructions of overpasses, which are high level road bridges. In specific, the tendons that create tension in order to suspend the bridge during construction follow design specifications based on Hooke's law. Even the skyscrapers and other tall buildings that we find ourselves in everyday include Hooke's law as a vital part of their design process. With different types of weather such as earthquakes or hurricanes, there is a possibility for huge forces to push on the buildings. The materials and geometry of the building are the factors in the stiffness of the building. The relationship between this stiffness and the force that pressures the building is summarized by Hooke's law, and in order to stay within it's limitations so the building doesn't collapse, architects must keep the law in mind during construction. Hooke's law holds a great importance in our lives whether or not we realize it.

History

Hooke's law was discovered by 17th century scientist Robert Hooke. Hooke was a British physicist who actually discovered this law in 1660 when he was working on designs for the springs of a clock. Originally, Hooke announced his discovery as "Ut tensio, sic vis" which is Latin for "As the extension, so the force," and this later became known as Hooke's law.

References

Universe Today [6]

Hyper Physics [7]

Hooke’s Law

Contents