Magnetic Dipole
Claimed by Zeynep Uzun (Fall 2025)
The Main Idea
A dipole is a pair of field producing entities placed close together to produce a particular pattern of field. In such cases it is useful to look a the pair as a single entity as a simplification as it allows us to create simple and commonly applicable equations for them as opposed to considering the two entities as separate. Dipoles also have a number of properties that shape the natural world in unique ways as the interactions of dipoles often create emergent properties.
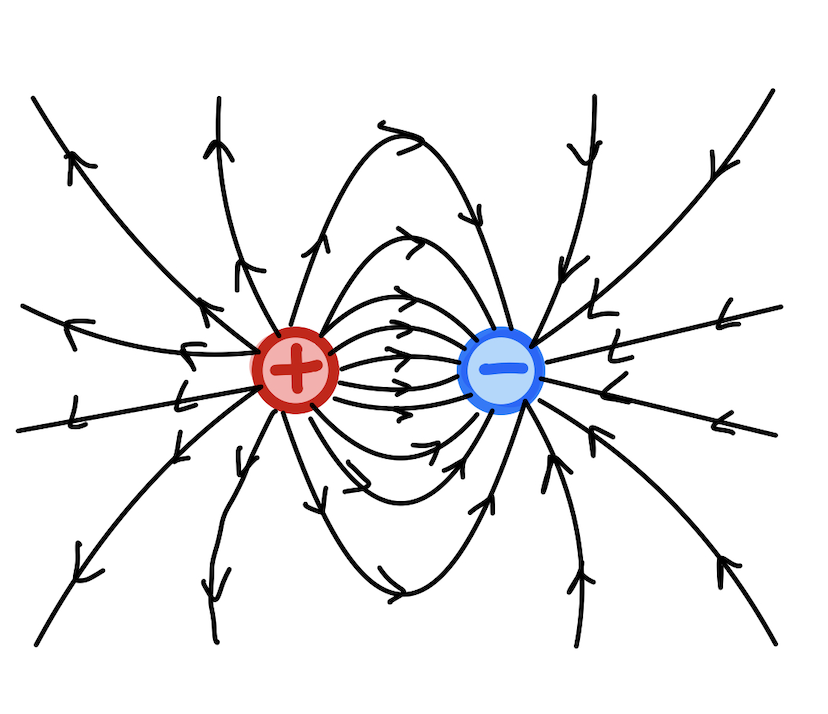
Physics students are typically taught about electric dipoles first, and will recognize that many of the properties and formulas resemble each other quite closely, This is because dipoles have the same field shape no matter what field they are influencing and so the same relationships between position and intensity exist with respect to the magnitudes of the charges.
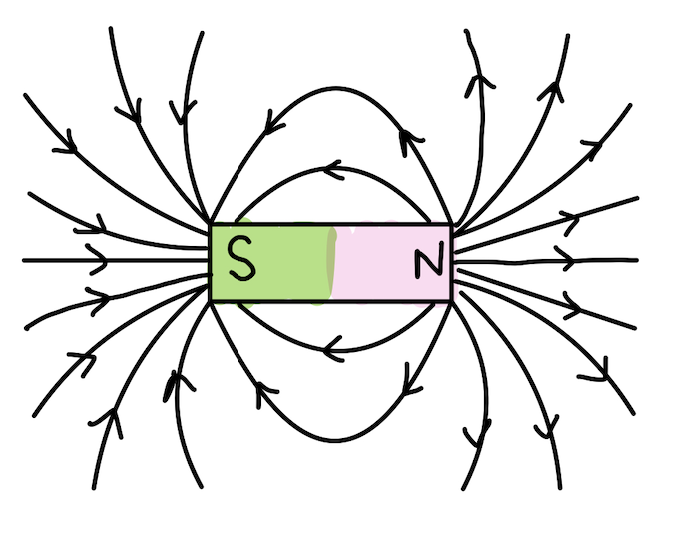
A common example of a macroscopic magnetic dipole is a common permanent magnet such as a bar magnet. These magnets will produce a magnetic field everywhere in space and the force varies only with observation position. This is very similar to an electric dipole, but instead of electrical charges, we have magnetic ones, represented by the North and South poles. Just like with positively and negatively charged ions, like charges repel, and opposite charges attract.
Since magnets always have two poles, the magnetic field produced is that of a magnetic dipole. The North pole is analogous to a positive charge and South to a negative charge, in that the field lines flow out from the North pole into the South pole.
Major Distinction from Electrical Dipoles
One major distinction between electrical and magnetic dipoles is the fact that while electrical "monopoles" exist in abundance in electrical charges, a magnetic monopole has never been confirmed to exist. This means that when talking about magnetism, we are essentially always talking in terms of dipoles and the dipole equations are used much more commonly than the formulas for individual magnetic charges. By using the formulas for dipoles, we can figure out the dipole moment of any magnet as long as we know our relative position and then we will have a reasonable model of any magnet that we can measure.
Bar magnets are what we typically think about when talking about dipoles, but there are a couple of other important constructs that create dipole magnetic fields. The other most notable magnetic dipole is the coil of wire with current flowing through it.
Connection With Magnetic Fields in Loops of Wire
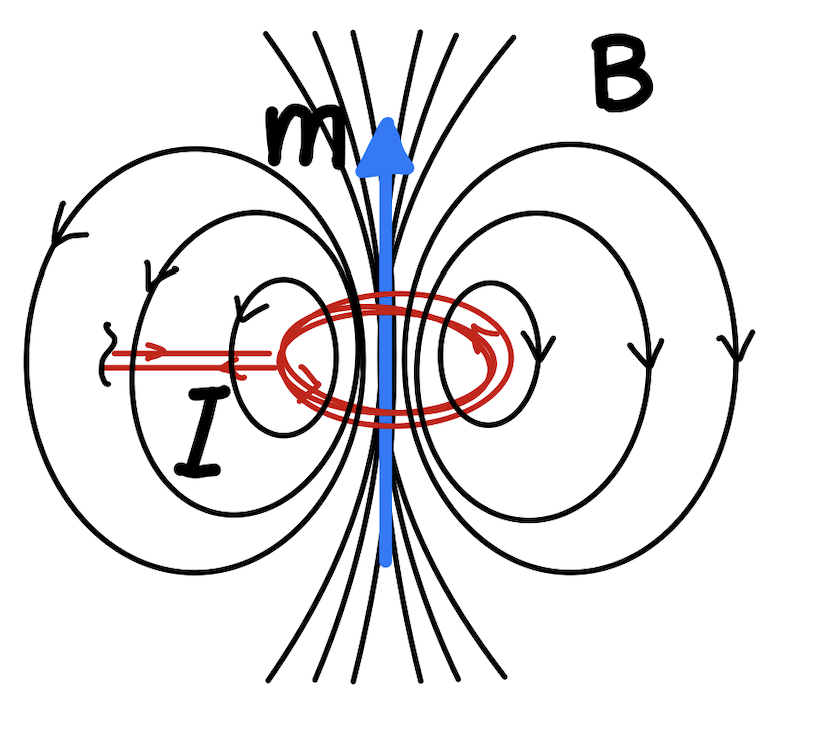
One of the most important things to recognize is the similarity between an obvious dipole like a bar magnet and what occurs when current flows through a loop of wire and how that allows us to perform calculations much easier. Current moving in a closed loop will create a dipole magnetic field as shown below.
We can see how this is similar to the field produced by particles(or equivalently by a permanent magnet)
One of the most important things to note about the dipole simplification is that it grants us the ability to calculate dipole moment, a measure of the polarity of the dipole, which aids in calculations regarding the energy and forces involved in iterating with the dipole. This is especially useful for dealing with current in a loop of wire, as it does not resemble a traditional dipole. Once you have the moment you can use all of the nice dipole formulas instead of trying to treat it as coils of wire.
Magnetic Dipole Moment and Connection with Torque on a Coil
The magnetic dipole moment represents the magnitude of the field of the dipole, essentially its magnetic potential.
The most common unit for the dipole moment is Ampere-square meters which is derived from how you calculate the moment of a coil of wire. It can also have the units of Joules per Tesla, representing the amount of energy per unit of magnetism an object will experience in the field of the dipole.
The magnetic dipole moment as it relates to current in coils of wire represents the torque on the current in the wire, which again is proportional to the magnitude of the magnetic field.
A Mathematical Model
A brief derivation:
From the Biot-Savart Law, we know that the magnetic field of a loop, when calculating the magnitude of the magnetic field at a point on the z-axis, is:
- [math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{(z^2 + R^2)^{3/2}} \text{ ,where R is the radius of the circular loop, and z is the distance from the center of the loop} }[/math]
An approximation can be made if the distance from the center of the loop is much greater than the radius of the loop (z >> R):
- [math]\displaystyle{ B = \frac{\mu_0}{4 \pi} \frac{2 \pi I R^2}{z^3} \text{ ,where z is much greater than R} }[/math]
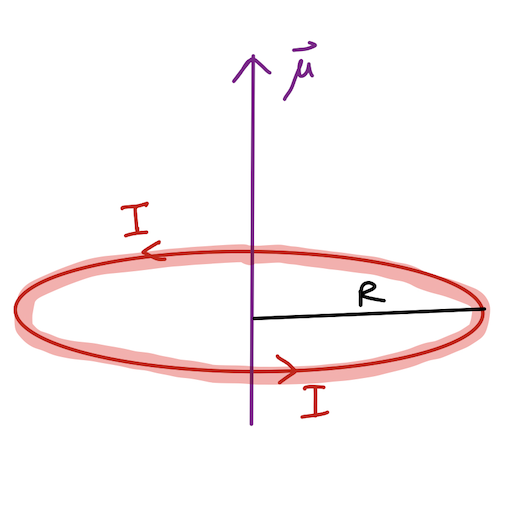
Given the magnetic dipole moment is current (I) multiplied by area (pi R^2), we can derive the magnetic dipole on axis as:
- [math]\displaystyle{ B = \frac{\mu_0}{4\pi} \frac{2\mu}{z^3} }[/math]
The equation for a magnetic dipole moment is:
[math]\displaystyle{ \boldsymbol{\mu} = \boldsymbol{IA} = \boldsymbol{I{\pi}R^2} }[/math] with units [math]\displaystyle{ A*m^2 }[/math]
where I is the current, and A is the cross sectional area. This will be used to calculate the magnitude of the magnetic field produced by a magnetic dipole.
The 2nd part of the equation is specifically for a circular loop field induced magnetic dipole and its area is the area of the loop.
From this equation, we can deduce the magnetic dipole moments just knowing the conventional current flowing through the loop and the radius.
However, most of the time the current is not given. Furthermore, the equation is not applicable for the normal bar magnets, for they do not have a electrical current flowing through. Thus, another way to get the dipole moment is by using the relationship between the magnetic dipole and the magnetic field induced by the dipole.
There are two equations based on the observation location.
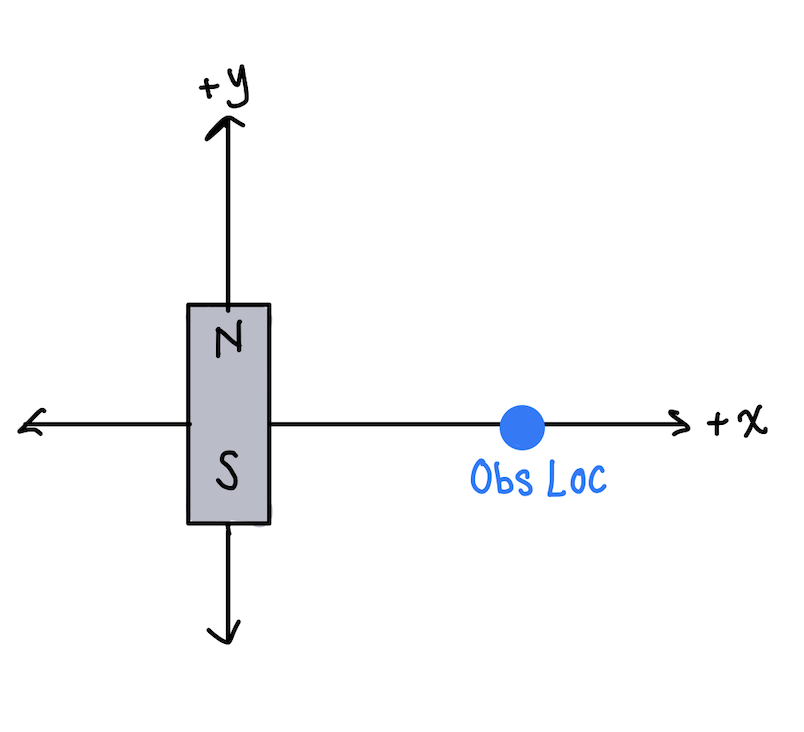
Observation Location Perpendicular to Dipole Axis
If the observation location is perpendicular to the axis of the dipole(see below),
then the equation for the magnetic field induced by the dipole is:
Note that this equation is analogous to the equation for an observation location perpendicular to the axis of an electric dipole. This is because magnetic dipoles and electric dipoles both have the same field shape.
Observation Location Along Dipole Axis
If the observation location is placed along the axis like in the image below,
then the equation for the magnetic field induced by the dipole is:
Note that this equation is analogous to the equation for an observation location perpendicular to the axis of an electric dipole. This is again because magnetic dipoles and electric dipoles both have the same field shape.
Direction of Dipole Moment
It is also important to note the direction of the dipole moment. In a bar magnet the dipole moment will be wrapping from the North end of the magnet until it faces the South end of the magnet in a traditional dipole fashion and field pattern.
On the other hand, if you are looking at the dipole moment induced by a current-flowing loop, you have to use the right hand rule. If you point your thumb in the direction of the current along the wire, your fingers will curl in the direction through the loop in the direction the magnetic field is flowing. Alternatively you can think about it another way and curl your fingers in the direction of the current, and your thumb will point in the direction of the magnetic dipole moment induced from the current.
Computational Model
The computational plot of a magnetic dipole is very similar to the plot of an electric dipole because of their similar forces. In some simulations, you can see a loop or coil of wire with the surrounding forces displayed using spaced vectors. In this simulation, you are able to move a dipole around and see in 3D how the dipole affects its surroundings with a constant magnetic field.
Click here for a glowscript model visualizing the magnetic field of a bar magnet in 2D. You may click and drag the blue magnet to see how the field changes.
Examples
Simple
- Example 1
- In a circular loop with current of 3 Ampere and diameter of 16 cm, what is the magnetic dipole moment induced from the current?
- Example 2
- What is the direction of the magnetic field at the observation location?
Click Expand for Solution
Example 1 Solution We can just simply use the first equation given in the beginning:
where R is 0.08 meters and I is 3 Amperes. Calculating for the magnetic dipole moment gives:
[math]\displaystyle{ 3 \times 0.08^2 \times \pi = 0.0192 A*M^2 }[/math]
Example 2 Solution First, identify the direction of the magnetic dipole moment. The magnetic dipole moment points from the S pole to the N pole, so mu is pointing in the positive y-hat direction. Because the observation axis is perpendicular, the magnetic field will point opposite to the mu direction. Thus, the magnetic field at the observation location points in the negative y-hat direction.
Middling
- Example 1
- When a compass is placed 20 cm away from a bar magnet parallel to the x-axis and shows deflection of 20 degrees, what is the magnitude of the magnetic dipole moment? You can assume that |Bearth| is [math]\displaystyle{ 2 \times 10^-5 T }[/math]
- Example 2
- A bar magnet is placed a distance 15 cm to the right of a compass that originally points North. After the magnet is placed next to the compass, the needle of the compass deflects 45 degrees to the west. What is the magnitude of the magnetic moment of the bar magnet? You can assume that |Bearth| is [math]\displaystyle{ 2 \times 10^-5 T }[/math]
Click Expand for Solution
Example 1 Solution
First, we need to figure out the magnetic dipole induced from the magnet. Thus, we need to use the formula:
where |Bearth| is [math]\displaystyle{ 2 \times 10^-5 T }[/math], and the deflection is 20 degrees. Thus,
[math]\displaystyle{ (2E-5 T) * tan(20) = 7.3E-6 T }[/math]
This gives us the magnitude of the magnetic field contributed by the bar magnet. We can plug in the value into the formula given (note that because it is along the x-axis, we use this formula)
[math]\displaystyle{ 7.3E-6 = \frac {1E-7 * 2 * \mu} {(0.2)^3} }[/math]
[math]\displaystyle{ \mu = 0.292 A*M^2 }[/math]
Example 2 Solution
Follow a similar process as described above. The solution is [math]\displaystyle{ \mu = 0.675 A*M^2 }[/math]
Difficult
- Example 1
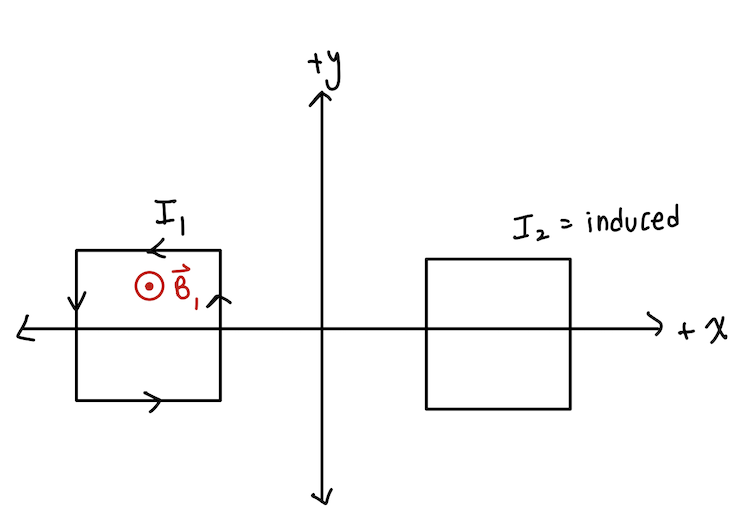
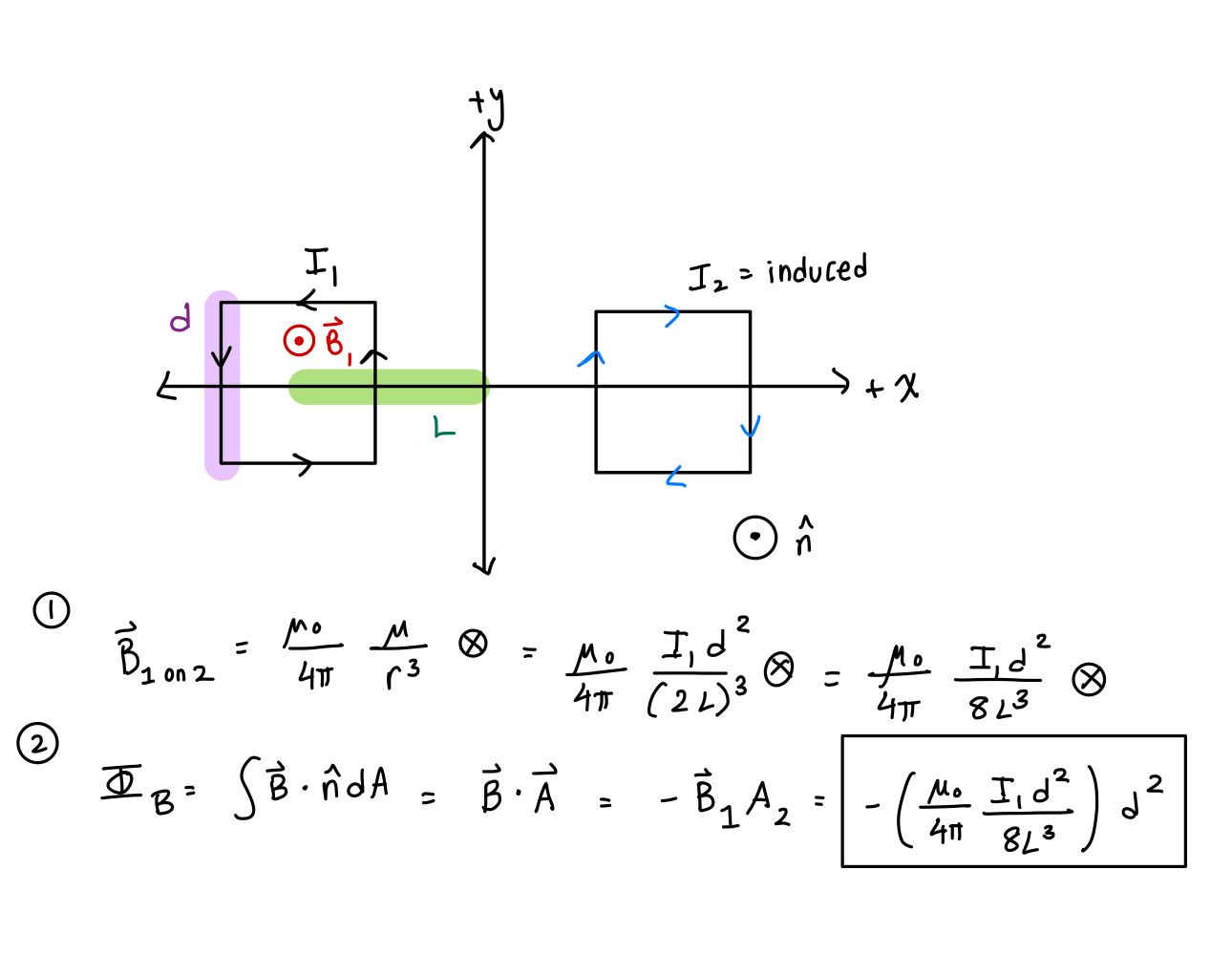
- Two identical square loops of wire have resistance R and sides of length d. The centers of the loop are equidistant from the origin at a distance L >> d. Loop 1 has a counterclockwise current flowing through it that is decreasing with time. What is the magnetic flux on the right loop? Define +n-hat as +z-hat. You need to have an understanding of magnetic flux for this problem.
Click Expand for Solution
Example 1 Solution First, identify the direction of the induced current on loop 2. A loop of current from far away looks like a magnetic dipole. So, at loop 2, the magnetic field from loop 1 is into the page. The current in loop 1 is decreasing, so the flux into the page at loop 2 is decreasing. When flux is decreasing, nature counteracts it by inducing a flux into the page stronger, which requires a clockwise current. Thus, I2 is clockwise. The magnetic field of loop 1 is of that of a dipole on the perpendicular axis. The magnetic dipole moment is current multiplied by area; use this in the equation.
Second, you need to find the flux. The magnetic field is into the page and n-hat is out of the page. This means the dot product result will be negative.
Here is the full solution:
Conceptual Questions
- If released from rest, what, if anything, will the current loop do?
Click Expand for Solution
The loop will rotate counterclockwise. We know this because the magnetic dipole moment has a tendency to want to align itself with any externally applied magnetic field, if one exists. Using the right-hand rule for a loop of current, we curl our fingers clockwise, causing our thumb to point straight downwards. This means that our magnetic dipole moment is poiting straight downwards. In order to align itself with the magnetic field that is pointing to the right, it must rotate counterclockwise.
Connectedness
Magnetic Flux and Degaussing Coils
As someone in the Navy ROTC Unit and joining the fleet someday, I like to learn about navigation and am currently enrolled in naval navigation. In this class we have looked at many different things about maneuvering but the most interesting was about open ocean navigation and use of the compass(link to section on geographic vs. magnetic north). In the times before gyro compasses and GPS calculations to find true north, sailors had to purely rely on their magnetic compass.
This was especially difficult due to the surrounding magnetic fields being emitted from the plethora of wires and equipment surrounding the compass on the bride and throughout the ship. So, in order to dampen the deviation of the compass created by the many different electric fields, the navy instituted what is called Degaussing Coils and spheres. These coils were strategically lined through the ship and the spheres were positioned directly next to the compass on opposite sides of the compass in order to cancel the surrounding magnetic field. These coils when used properly create a magnetic dipole.
In some robotics applications, like robotic soccer in my case, we use solenoids to rapidly accelerate iron cores to kick soccer balls at high velocities. The precise calculations to figure out how much acceleration the core is under and how the magnetic field affects it are immensely complex and require a lot of compute power and time, but we can use the dipole moment calculation to get a decent idea of how much energy is being imparted and a rough idea of the acceleration we are dealing with in order to figure out how long to energize the coil to get the ball to a specific velocity.
Industrial Application
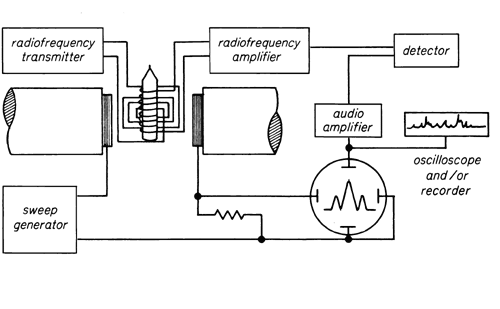
One of the most common industrial applications of Magnetic Dipole is the Nuclear Magnetic Resonance spectroscopy. To learn more about NMR, click here
Dipole-like fields are found anywhere there is a coil of wire, that is to say in many electronic applications such as electric motors, transformers, chokes, and many other electronic components. The dipole simplification of magnetic field calculations makes it much easier to calculate for these devices although with the prevalence of computer models more accurate calculations can be performed.
History
Discovery
The discovery of magnetic dipoles is mostly attributed to | André-Marie Ampère. Ampere began theorizing about magnetic dipoles when he discovered that current loops produce magnetic fields. Initially, he thought that all magnetic fields result from loops of current. This discovery laid the basis of later work that was able to quantify and explain magnetic fields.
Ampere hails form Lyon, France and his early life was shaped by the French Revolution. His father was a judge, and beheaded by the revolutionaries. Ampere found himself unable to continue his education after the death of his father, but eventually found himself able to return to his studies. Ampere was married to Julie Carron, and had one some with her named Jean-Jacques Ampère. Their son would later grow up to be a famous historian and writer.
Magnetic Monopoles
Although electrostatics and magnetics have a lot in common, one difference is that magnetic poles cannot exist singly like charges can. Poles always come in N/S pairs. If you were to cut a bar magnet in half, you will get two new magnets with North and South poles.
A magnetic monopole was observed once, by | Blas Cabrera, on February 14, 1982 (also known as the Valentine's Day Monopole). However, this experiment has been recreated several times, and no one, not even Cabrera himself, has been able to find another monopole.
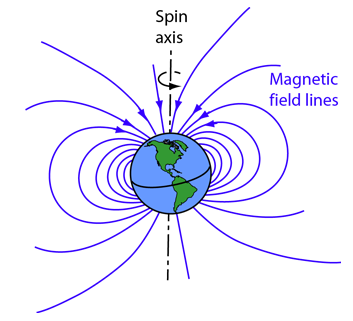
Magnetic North vs Geographic North
There is a common misconception about the magnetic field of the earth and the geographical north pole. The geographical north pole is home to the magnetic south pole and vise versa. However, the magnetic and geographical poles are not located in the same place on the planet. This means that while a compass is the first thing that comes to mind when people think about navigation, it is not an effective means of navigation when nearing the poles or in the waters of the far north or south. Below in the Further reading section, there is an in depth article about the positioning of the magnetic and geographical poles, how they came to be, and the effect they have had on the world.
See also
Magnetic Field of a Long Straight Wire
Further reading
Terahertz Magnetic Response from Artificial Materials