Poynting Vector
Claimed by Tanner Shaw (tshaw30)
The Poynting vector represents the direction and magnitude of the flux in energy from an electromagnetic field. It was originally discovered by John Henry Poynting in 1884.
The Main Idea
The poynting vector describes the magnitude and direction of the flux in energy from an electromagnetic field. It is measured in units of Watts per meter squared ([math]\displaystyle{ \frac{W}{m^2}) }[/math]. It can be used to determine in what direction energy is travelling from a source of electromagnetic radiation, such as a moving charged particle, an antenna, etc.
A Mathematical Model
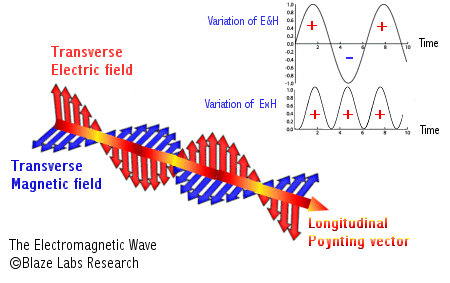
The poynting vector can be derived by the equation
[math]\displaystyle{ \vec{S} = {\frac{1}{μ_0}}\vec{E}\times\vec{B} }[/math]
where E is the electric field vector, and B is the magnetic field vector, and μ0 is the magnetic constant. A cross product is needed to compute the poynting vector, so being familiar with the right-hand-rule can help to conceptualize and/or check your answer for problems asking to find it.
A Computational Model
The poynting vector can be used to predict the direction of energy movement in many different scenarios. Anything that produces electromagnetic waves can have the flux of energy produced from it mapped. One common example is an antenna broadcasting radio waves. A good demonstration of the potential for poynting vectors can be seen from Wolfram Alpha's Demonstration of Electromagnetic Waves from an Antenna. This demo requires the download of their Wolfram CDF player. In the demonstration, you can adjust variables such as the length of the antenna, peak current in the antenna, etc., and see how it affects poynting vectors in the space around the antenna.
Examples
Simple
An electron is travelling in the -X direction in the XY plane. At a certain instant, you observe the electron from a location as seen in the diagram. What is the direction of the poynting vector from your location?
The equation for finding the poynting vector is given as [math]\displaystyle{ \vec{S} = {\frac{1}{μ_0}}\vec{E}\times\vec{B} }[/math]. Therefore, a cross product of the electric field vector and the magnetic field vector at the observation location must be taken. This will require the concept of right-hand-rule. The electric field from the observation location points towards the electron, in the +X and +Y directions.
The magnetic field can be found by using the right-hand-rule of the velocity of the electron and the position vector. The electron is moving in the -X direction, and the position vector points in both the -X and -Y directions. Using right-hand-rule, the cross product of those two vectors will point in the +Z direction.
As the electric field vector points in the +X and +Y directions, and the magnetic field points in the +Z direction, using right-hand-rule, the poynting vector will point in the directions +X and -Y.
Moderate
A proton is moving in the +X direction at two thirds the speed of light in the XY plane. At a certain instance, your observation location is 3e-8 m in the -Y direction from the proton. Calculate the poynting vector at this observation location from the moving proton.
In order to solve this problem, we must calculate both the electric and magnetic fields caused by the moving particle at the observation location. To solve for the electric field we will use the formula for calculating electric fields from point charges, [math]\displaystyle{ \vec{E} = {\frac{1}{4πε_0}}{\frac{Q}{r^2}}\hat{r} }[/math].
Therefore, we must solve:
[math]\displaystyle{ \vec{E} = (9\times10^9\frac{N\times m^2}{C^2}){\frac{(1.6\times10^{-19} C)}{({3\times10^{-8} m})^2}} \lt 0,-1,0\gt }[/math]
Which will give us:
[math]\displaystyle{ \vec{E} = \lt 0, 1.6\times10^6,0\gt \frac{N}{C} }[/math]
Now that we have the electric field at the observation location, all we have left to calculate is the magnetic field. The equation of the magnetic field due to a moving point charge is [math]\displaystyle{ \vec{B} = {\frac{μ_0}{4π}} Q{\frac{\vec{v}\times\hat{r}}{r^2}} }[/math].
Therefore, we must solve:
[math]\displaystyle{ \vec{B} = (1\times10^{-7}{\frac{T\times m}{A}})(1.6\times10^{-19}C){\frac{\lt 2\times10^8,0,0\gt {\frac{m}{s}} \times\lt 0,-1,0\gt }{(3\times10^{-8}m)^2}} }[/math]
Which gives us:
[math]\displaystyle{ \vec{B} = \lt 0,0,-3.56\times10^{-3}\gt T }[/math]
Using the equation [math]\displaystyle{ \vec{S} = {\frac{1}{μ_0}}\vec{E}\times\vec{B} }[/math], we can find the answer.
[math]\displaystyle{ \vec{S} = (\frac{1}{4π\times10^{-7}})\lt 0, 1.6\times10^6,0\gt \frac{N}{C}\times\lt 0,0,-3.56\times10^{-3}\gt T }[/math]
[math]\displaystyle{ \vec{S} = \lt -4.53\times10^9, 0, 0\gt \frac{W}{m^2} }[/math]
Difficult
A proton and an electron are moving in 3D space. At one point in time, the proton is located on the Z axis at <0,0,4e-8>m and is travelling in the +Y direction at 1/3 the speed of light. At the same point in time, the electron is located at <3e-8, 3e-8, 0>m and is travelling in the +X direction at 2/3 the speed of light. Find the net poynting vector at the origin due to both the proton and electron.
In order to solve this problem, we will have to take many steps. We must find the poynting vector at the origin caused by the proton by finding the electric field and magnetic field it produces at that point. Then, we must do the same for the electron. Finally, we can sum the two vectors together and find the net poynting vector.
We will start this problem by focusing on the proton. To solve for the electric field we will use the formula for calculating electric fields from point charges, [math]\displaystyle{ \vec{E} = {\frac{1}{4πε_0}}{\frac{Q}{r^2}}\hat{r} }[/math].
Therefore, we must solve:
[math]\displaystyle{ \vec{E_p} = (9\times10^9\frac{N\times m^2}{C^2}){\frac{(1.6\times10^{-19} C)}{({4\times10^{-8} m})^2}} \lt 0,0,-1\gt }[/math]
Which gives us:
[math]\displaystyle{ \vec{E_p} = \lt 0,0,-9e5\gt \frac{N}{C} }[/math]
Now that we have the electric field at the observation location, we must calculate the magnetic field caused by the proton. The equation of the magnetic field due to a moving point charge is [math]\displaystyle{ \vec{B} = {\frac{μ_0}{4π}} Q{\frac{\vec{v}\times\hat{r}}{r^2}} }[/math].
Therefore, we must solve:
[math]\displaystyle{ \vec{B_p} = (1\times10^{-7}{\frac{T\times m}{A}})(1.6\times10^{-19}C){\frac{\lt 0,1\times10^8,0\gt {\frac{m}{s}} \times\lt 0,0,-1\gt }{(4\times10^{-8}m)^2}} }[/math]
Which will give us:
[math]\displaystyle{ \vec{B_p} = \lt -1\times10^{-3},0,0\gt T }[/math]
Now that we have the poynting vector caused by the proton, we must find the poynting vector caused by the electron. First, we will find the electric field caused by the electron.
Now using the equation [math]\displaystyle{ \vec{S} = {\frac{1}{μ_0}}\vec{E}\times\vec{B} }[/math], we can find the poynting vector caused by the proton at the origin.
[math]\displaystyle{ \vec{S_p} = (\frac{1}{4π\times10^{-7}})\lt 0,0,-9e5\gt \frac{N}{C}\times\lt -1\times10^{-3},0,0\gt T }[/math]
[math]\displaystyle{ \vec{S_p} = \lt 0, 7.162\times10^8, 0\gt \frac{W}{m^2} }[/math]
Now that we have found the poynting vector for the proton, we must now find the poynting vector for the electron. First we will find the electric field caused by the electron.
[math]\displaystyle{ \vec{E_e} = (9\times10^9\frac{N\times m^2}{C^2}){\frac{(-1.6\times10^{-19} C)}{({4.243\times10^{-8} m})^2}} \lt -0.707,-0.707,0\gt }[/math]
[math]\displaystyle{ \vec{E_e} = \lt 5.657e5, 5.657e5,0\gt \frac{N}{C} }[/math]
Now, we will find the magnetic field caused by the electron at the origin.
[math]\displaystyle{ \vec{B_e} = (1\times10^{-7}{\frac{T\times m}{A}})(-1.6\times10^{-19}C){\frac{\lt 2\times10^8,0,0\gt {\frac{m}{s}} \times\lt -0.707,-0.707,0\gt }{(4.243\times10^{-8}m)^2}} }[/math]
[math]\displaystyle{ \vec{B_e} = \lt 0,0,1.26\times10^{-3}\gt T }[/math]
Now that we have both the electric and magnetic field caused by the electron, we can find it's poynting vector.
[math]\displaystyle{ \vec{S_e} = (\frac{1}{4π\times10^{-7}})\lt 5.657e5, 5.657e5,0\gt \frac{N}{C}\times\lt 0,0,1.26\times10^{-3}\gt T }[/math]
[math]\displaystyle{ \vec{S_e} = \lt 5.672\times10^8,-5.672\times10^8, 0\gt \frac{W}{m^2} }[/math]
And so the net poynting vector at the origin is:
[math]\displaystyle{ \vec{S} = \lt 5.672\times10^8,1.490\times10^8, 0\gt \frac{W}{m^2} }[/math]
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

John Henry Poynting, an English physicist and professor, was the first to derive the equation that described the direction of electromagnetic flux. His work for the equation was published in 1884. Nikolay Umov and Oliver Heaviside both independently discovered the poynting vector as well. Interestingly, Nikolay Umov supposedly published his work that proved the poynting vector, however it was in a more generalized perspective.
Poynting used his work to help prove his theory discussing the conservation of energy in electromagnetic fields, aptly named Ponyting's Theorem. According to Wikipedia, Poynting's states that:
- The rate of energy transfer (per unit volume) from a region of space equals the rate of work done on a charge distribution plus the energy flux leaving that region.
Which in even simpler terms means that the energy transfer in an electromagnetic field is balanced.
See also
External links
DrPhysicA's YouTube video on Poynting Vectors