Torque
This is now claimed by Rayed Chowdhury (Fall 2024).
Torque is the measure of how much a force acting on an object causes that object to rotate, creating a tendency for the object to rotate about an axis, fulcrum, or pivot. Torque is most commonly classified as "twist", rotational force, or angular force to an object and applying it to a system changes the angular momentum of the system. The effectiveness of torque depends on where the force is applied and the position at which the force acts relative to a location.
History
The concept of torque first originated with Archimedes study on levers. While he did not invent the lever, his research and work on it caused him to create the block-and-tackle pulley systems, allowing people to use the principle of leverage to lift heavy objects. Building off of this, he explained how torque comes into play with objects that are twisting or rotating around a pivot, just as a lever does around the point of rotation. Using the Law of the Lever and geometric reasoning, Archimedes developed the concept of torque.
In 1884, the term "torque" was introduced into English scientific literature by James Thomson, a notable scientist remembered for his work on the improvement of water wheels, water pumps, and turbines. Before officially introducing the name torque, the twisting or torsional motion was referred to "moment of couple" or "angular force".
Modeling and Understanding
A Mathematical Model
Torque is the cross product between the distance vector, a vector from the point of pivot (A) to the point where the force is applied, and the force vector. The force vector, [math]\displaystyle{ {\vec{F}} }[/math], is defined about a particular location.
When applying a force to an object at an angle [math]\displaystyle{ {\theta} }[/math] to the radius, a different equation is required to capture both the force of the twist and the distance from the pivot point to the place where the force is applied. This equation finds the magnitude of torque exerted by a force, [math]\displaystyle{ {\vec{F}} }[/math] relative to a location (A).
For a purely perpendicular force with a force application at [math]\displaystyle{ {\theta}=90{º} }[/math], [math]\displaystyle{ sin{\theta}=1 }[/math] and the torque is rAF. For a force that is parallel to the lever arm at an angle [math]\displaystyle{ {\theta}=0{º} }[/math], [math]\displaystyle{ sin{\theta}=0 }[/math] and the torque is zero.
Angular Acceleration
Net torque on a system is also equal to the moment of inertia multiplied by the angular acceleration.
Angular Momentum Principle
The equation for torque is derived from the Angular Momentum Principle, which states that torque is equal to the change in length over time. Another equation used to represent torque is
Units
The SI unit of torque is the newton meter [math]\displaystyle{ {N{\bullet}m} }[/math] or joule per radian [math]\displaystyle{ {J/rad} }[/math]. These units are produced from the dot product of a force and the distance over which it acts.
Addition and Subtraction
If more than one torque acts on an object, these values can be combined to calculate the overall net torque. If the torques make the object spin in opposite directions, they should be subtracted from one another. If the individual torques make an object spin in the same direction, the values should be added together.
Direction of the Force
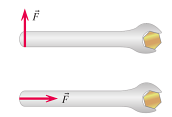
When applying a force to a system, the direction of the force greatly affects the torque and alters the effectiveness of twisting. As seen, a force parallel to the handle or object using to twist another is extremely ineffective and does not produce a torque. When the force only contains a perpendicular component, it is effective at twisting an object.
Point of Application of the Force
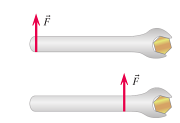
The point and placement of application of the force on an object also affects who effective the torque is. The further away from the point of rotation that a force is applied, the more effective the twist is. In order to make your twisting most effective, add length to provide more leverage.
Direction of Torque
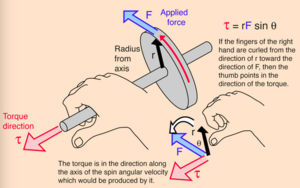
Because torque is a vector quantity, it is important to determine the direction in which torque occurs. The direction of torque is perpendicular to the radius from the axis and the force being applied to the system. The right-hand rule along the axis of rotation can be used to determine the direction of torque, where torque is in the direction your thumb is pointing. Torque is in the same direction of the change in angular velocity.
Put the fingers of the right hand in the direction of the distance vector (r) and curl the fingers in the direction of the force vector (F). The direction of the torque vector will be in the direction that the thumb is pointing towards.
If the motion is counterclockwise, and the thumb is pointing "out" from the page, the direction of torque can be noted with a "bullseye" pictogram. If the motion is clockwise, and the thumb is pointing "into" the page, the direction can be noted with an "X" pictogram.
Examples
Simple
Problem
A force of 50 N is applied to a wrench that is 30 cm in length. Calculate the torque if the force is applied perpendicular to the wrench.
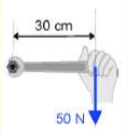
Solution
Using Equation 1, [math]\displaystyle{ {\vec{\tau}} = {\vec{r}} \times {\vec{F}} }[/math], you can plug in the values given for distance from point of rotation to where the force is being applied and for force.
Middling
Problem
Solution
Using Equation 2, plug in the values for [math]\displaystyle{ r_A }[/math], [math]\displaystyle{ F }[/math], and \theta.
Difficult
Problem

Solution
First, create a free body diagram to include all of the forces acting on the system. Using the standard coordinate system, the pivot location is A.
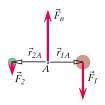
In order to get the net torque, calculate all of the individual torques about the location A and add them up.
Torque due to child 1:
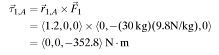
The magnitude of the torque of child 1 can be found by putting the distance vector and the force vector tail to tail and applying the right hand rule. It is found that the direction of the torque is into the page in a -z direction.
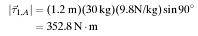
Torque due to child 2:
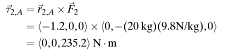
The cross product of normal force, [math]\displaystyle{ {\vec{F}}_n }[/math], and total direction vector, [math]\displaystyle{ {\vec{r}}_n,A }[/math], can be used to find the net torque about the point of rotation, A. The torque due to the normal force is zero because the force acts at location A, so it can't twist the seesaw.
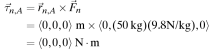
The net torque of the system is:
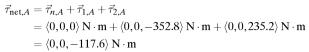
For a brief introduction on a different method of calculating cross products (using matrices and cofactor expansion), watch this video: [1] (Useful for when vectors don't happen to line up neatly on the XYZ planes).
"radius" vector in the video refers to the distance vector (r). Please visit this glow script model to play around with calculating the cross product: https://trinket.io/glowscript/65b87c8e43
Examples with Computational Models
Torque is not only modeled mathematically but also computationally to simulate real-world applications and interactions. Computational tools such as MATLAB, Python, and Glowscript and in doing so Torque problems can even be simplified and a lot easier to understand.
One key benefit of computational methods is the simplification of vector operations, such as cross products or dot products, which are foundational to torque calculations. Manually computing these can be error-prone, especially in 3D systems, but tools like Python’s numpy library automate these processes with precision, making the calculations faster and more reliable.
Below are some examples of problems where code snippets are used to help evalutate our answer.
Problem 1
Rotating Disk:
A solid disk with a mass of 2 kg and a radius of 0.5 m is initially at rest. A constant tangential force of 5 N is applied at the edge of the disk.
a) Calculate the torque applied to the disk.
b) Determine the angular acceleration of the disk.
c) Use Glowscript to simulate the rotational motion of the disk over 5 seconds.
Solution:
a) Calculating Torque (τ)
Torque is given by:
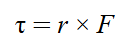
Since the force is applied tangentially at the edge,
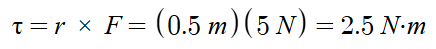
b) Determining Angular Acceleration (𝛼)
The moment of inertia for a solid disk in this case:
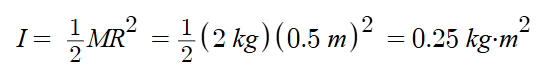
Using Newton's second law for rotation:
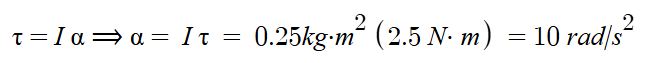
c) Glowscript Simulation
Below is the Glowscript code to simulate the rotational motion of the disk.
GlowScript 3.0 VPython
# Visualization
disk = cylinder(pos=vector(0,0,0), axis=vector(0,0.01,0), radius=0.5, color=color.blue)
pivot = sphere(pos=vector(0,0,0), radius=0.02, color=color.red)
# Physical Properties
M = 2 # Mass in kg
R = 0.5 # Radius in meters
I = 0.5 * M * R**2 # Moment of inertia for a solid disk
# Applied Force
F = 5 # Force in Newtons
tau = R * F # Torque = r x F
alpha = tau / I # Angular acceleration
# Initial Conditions
theta = 0 # Initial angle
omega = 0 # Initial angular velocity
t = 0 # Time
dt = 0.01 # Time step
# Simulation Loop
while t < 5:
rate(100)
# Update angular velocity and angle
omega += alpha * dt
theta += omega * dt
# Rotate the disk
disk.rotate(angle=omega*dt, axis=vector(0,0,1), origin=pivot.pos)
# Advance time
t += dt
Connectedness
Torque exists almost everywhere we go and is involved in nearly everything we do. If torque didn't exist, we would only be able to do things linearly in a uniform line and there wouldn't be spin, turn, or circular motion. Actions such as turning a steering wheel or opening a bottle would be impossible without the twisting motion we call torque.
The concept of torque interests me greatly as a Chemical Engineering major because torque plays a role in most chemical processes and unit operations. Using torque for reactions can alter flow rates, create shaft work, and affect the energy balances of continuous, steady state systems.
Torque has many industrial applications in industries such as aerospace, automotive, material processing, medical, robotics, oil and gas, and assembly. It is often used in finishing off materials with operations such as polishing, grinding, and deburring. Torque sensors are often used to determine the amount of power of engines, motors, turbines, and other rotating devices and the sensors make the required torque measurements automatically on many assembly and sure machines.
