Magnetic Field of a Disk: Difference between revisions
No edit summary |
|||
| (18 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
'''Claimed by MaKenna Kelly Fall 2021''' | |||
==Main Idea== | ==Main Idea== | ||
On this page, we will explore how to solve for the magnetic field produced by a rotating, charged, circular disk. | |||
First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object | First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object can produce unique electric fields. | ||
In order to figure out | In order to figure out the magnetic field of a disk, we will start from the fundamental principles that we have learned already with regards to how magnetic fields are produced. We will then build on that and include the geometry of the object in question, in this a circular disk, in order to solve for the magnetic field produced by a disk. | ||
===Mathematical Model=== | ===Mathematical Model=== | ||
| Line 48: | Line 50: | ||
===Computational Model=== | ===Computational Model=== | ||
:: | Click the "1" on the right to view and/or edit a computational model of a disk's magnetic field. [https://www.glowscript.org/#/user/makennak/folder/MyPrograms/program/PHYS2Wiki] | ||
[[File:Disk_model_preview.JPG]] | |||
Notes about the model: | |||
- the disk is represented by the gray object in the center of the screen | |||
- the arrows represent the magnetic field created by the disk at different observation locations | |||
- the orange arrow represents B1 (magnetic field to the right of the disk) | |||
- the red arrow represents B2 (magnetic field above the disk) | |||
- the green arrow represents B3 (magnetic field to the left of the disk) | |||
- the blue arrow represents B4 (magnetic field below the disk) | |||
Model made by MaKenna Kelly (undergraduate student and an editor of this page) | |||
==Examples== | ==Examples== | ||
| Line 106: | Line 128: | ||
===Middling=== | ===Middling=== | ||
A uniformly charged disk of radius <math>R = 0.01 \ \text{m}</math> is rotating at a rate of <math>\omega = 2\pi \ \frac{\text{rads}}{s}</math> and is losing its charge to its surroundings in such a way that the charge density of the disk is | A uniformly charged disk of radius <math>R = 0.01 \ \text{m}</math> is rotating at a rate of <math>\omega = 2\pi \ \frac{\text{rads}}{s}</math> and is losing its charge to its surroundings in such a way that the charge density of the disk is increasing by <math>\frac{d \sigma}{dt} = \pi te^{-\frac{5t^2}{\pi}}</math>, where <math>t</math> is time in seconds. | ||
:'''a) What is the magnitude of the magnetic field at time <math>t_0 = 0</math> along the axis of rotation, if the charge density is <math>3 \ \frac{C}{A}</math> at this time?''' | :'''a) What is the magnitude of the magnetic field at time <math>t_0 = 0</math> along the axis of rotation, if the charge density is <math>3 \ \frac{C}{A}</math> at this time?''' | ||
| Line 133: | Line 155: | ||
:'''b) What is the magnetic field at time <math>t_f = 10 \ s</math> ?''' | :'''b) What is the magnetic field at time <math>t_f = 10 \ s</math> ?''' | ||
::To find the magnitude of the magnetic field, we will have to find the new charge density, since we were told it is increasing with time. To do this, we will integrate <math>\frac{d \sigma}{dt}</math> to solve for <math>\sigma (t)</math>: | |||
:::<math>\frac{d \sigma}{dt} = \pi te^{-\frac{5t^2}{\pi}}</math> | |||
::'''or''': | |||
:::<math>d \sigma = \left[ \pi te^{-\frac{5t^2}{\pi}} \right] dt</math> | |||
::'''or''': | |||
:::<math>\int d \sigma = \int \pi te^{-\frac{5t^2}{\pi}} \ dt</math> | |||
::'''or''': | |||
:::<math>\begin{align} | |||
\sigma (t) & = \int \pi te^{-\frac{5t^2}{\pi}} \ dt \\ | |||
& = \pi \int te^{-\frac{5t^2}{\pi}} \ dt \\ | |||
& = \pi \int -\frac{\pi}{10} e^u du \ \text{ where } u = -\frac{5t^2}{\pi} \text{ and } du = -\frac{10}{\pi} t \ dt \\ | |||
& = -\frac{\pi^2}{10} \int e^u du \\ | |||
& = -\frac{\pi^2}{10} \left[e^u \right] + C\\ | |||
\sigma (t) & = -\frac{\pi^2}{10} \left[e^{-\frac{5t^2}{\pi}} \right] + C \\ | |||
\end{align}</math> | |||
::To find <math>C</math> we use the original charge density of time <math>t_0 = 0</math>: | |||
:::<math>\sigma (0) = 3</math> | |||
::Therefore: | |||
:::<math>3 = -\frac{\pi^2}{10} \left[e^{-\frac{5(0)^2}{\pi}} \right] + C</math> | |||
:::<math>C = 3 + \frac{\pi^2}{10}</math> | |||
::This gives <math>\sigma (t)</math> as: | |||
:::<math>\begin{align} | |||
\sigma (t) & = -\frac{\pi^2}{10} \left[e^{-\frac{5t^2}{\pi}} \right] + 3 + \frac{\pi^2}{10} \\ | |||
\sigma (t) & = \frac{\pi^2}{10} \left[1 - e^{-\frac{5t^2}{\pi}} \right] + 3 \\ | |||
\end{align}</math> | |||
::Now we can find <math>\sigma (10)</math>: | |||
:::<math>\sigma (10) = \frac{\pi^2}{10} \left[1 - e^{-\frac{5(10)^2}{\pi}} \right] + 3</math>: | |||
::This gives: | |||
:::<math>\sigma (10) \approx 4 \ \frac{C}{A}</math> | |||
::Now we can find the magnetic field generated by the rotating disk: | |||
:::<math>B(z) = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right]</math> | |||
:::<math>B(z) = \left(1.58 \times 10^{-5} \right) \left[\frac{2z^2 + \left(1 \times 10^{-4}\right)}{\sqrt{z^2 + \left(1 \times 10^{-4}\right)}} - 2|z| \right]</math> | |||
===Difficult=== | ===Difficult=== | ||
Two concentric infinitely thin disks are rotating in opposite directions in the xy-plane. Disk 1 <math>(D_1)</math> is the inner disk, with a radius of <math>R_1 = 1 \text{ m}</math>; it is rotating counter-clockwise at a rate of <math>\omega_1 = 10 \ \frac{\text{rads}}{s}</math>. Disk 2 <math>(D_2)</math> is the outer disk, with a radius of <math>R_2 = 5 \text{ m}</math>; it is rotating clockwise at a rate of <math>\omega_2 = 3 \ \frac{\text{rads}}{s}</math>. See [https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&ved=2ahUKEwitqJugrJ7kAhXMnOAKHfcUAXUQjRx6BAgBEAQ&url=https%3A%2F%2Fwww.semanticscholar.org%2Fpaper%2FA-Genetic-Algorithm-Evolved-3D-Point-Cloud-Wegrzyn-Alexandre%2F078bbb2095973f453b1dc54d1aa37f8d481e39ce%2Ffigure%2F2&psig=AOvVaw2PgbcgTIJOxLJT2fwkXCQc&ust=1566833588588092] for clarification. | Two concentric infinitely thin disks are touching and rotating in opposite directions in the xy-plane. Disk 1 <math>(D_1)</math> is the inner disk, with a radius of <math>R_1 = 1 \text{ m}</math>; it is rotating counter-clockwise at a rate of <math>\omega_1 = 10 \ \frac{\text{rads}}{s}</math>. Disk 2 <math>(D_2)</math> is the outer disk, with a radius of <math>R_2 = 5 \text{ m}</math>; it is rotating clockwise at a rate of <math>\omega_2 = 3 \ \frac{\text{rads}}{s}</math>. Their charge density is <math>\sigma = 20 \ \frac{C}{A}</math> See [https://www.google.com/url?sa=i&rct=j&q=&esrc=s&source=images&cd=&ved=2ahUKEwitqJugrJ7kAhXMnOAKHfcUAXUQjRx6BAgBEAQ&url=https%3A%2F%2Fwww.semanticscholar.org%2Fpaper%2FA-Genetic-Algorithm-Evolved-3D-Point-Cloud-Wegrzyn-Alexandre%2F078bbb2095973f453b1dc54d1aa37f8d481e39ce%2Ffigure%2F2&psig=AOvVaw2PgbcgTIJOxLJT2fwkXCQc&ust=1566833588588092] for clarification. Ignore any frictional or electromagnetic effects the disks may have on each other. | ||
:'''a) What is the direction of the magnetic field created by <math>D_1</math> at a point along the axis of rotation and above the disk? What is the direction of the magnetic field created by <math>D_2</math> at a point along the axis of rotation and above the disk?''' | :'''a) What is the direction of the magnetic field created by <math>D_1</math> at a point along the axis of rotation and above the disk? What is the direction of the magnetic field created by <math>D_2</math> at a point along the axis of rotation and above the disk?''' | ||
::Using the right-hand rule, we see the two rotating disks are creating opposing magnetic fields; <math>D_1</math> creates a field pointing straight up along the axis of rotation. <math>D_2</math> creates a magnetic field pointing straight down along the axis of rotation. | |||
:'''b) What is the magnitude of the net magnetic field <math>0.13 \text{ m}</math> along the axis of rotation and above the disks?''' | :'''b) What is the magnitude of the net magnetic field <math>0.13 \text{ m}</math> along the axis of rotation and above the disks?''' | ||
::We can answer this question by solving for each magnetic field separately and then summing them (taking their directions into account). The major impediment is that the general formula: | |||
:::<math>B_z = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right]</math> | |||
::will not work for the outer disk <math>D_2</math>. This is because in the derivation, we integrated from <math>r = 0</math> to <math>r = R</math>. For <math>D_2</math>, we must integrate from <math>r = R_1</math> to <math>r = R_2</math>, since those are its radial bounds. The formula will work as usual for <math>D_1</math>. | |||
::Going back to the third to last step of the derivation, we have: | |||
:::<math> B = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}}</math> | |||
::We will correct this for <math>D_2</math> by replacing <math>r = 0</math> by <math>r = R_1</math>: | |||
:::<math> B = \frac{\mu_0 \sigma\omega}{2} \int_{R_1}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}}</math> | |||
::Of course the integral will be the same as before, but with different bounds: | |||
:::<math> B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{R_1}^{R}</math> | |||
:::<math>B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - \frac{2z^2 + {R_1}^2}{\sqrt{z^2 + {R_1}^2}} \right]</math> | |||
::Therefore, the magnetic field created by <math>D_2 \ 0.13 \text{ m}</math> along the axis of rotation and above the disks is: | |||
:::<math>B_{D_2} = \frac{\mu_0 \times 20 \times 3}{2} \left[\frac{2(0.13)^2 + (5)^2}{\sqrt{(0.13)^2 + (5)^2}} - \frac{2(0.13)^2 + (1)^2}{\sqrt{(0.13)^2 + (1)^2}} \right]</math> | |||
:::<math>B_{D_2} = 1.5 \times 10^{-4} \text{ T}</math> | |||
::To find the magnetic field due to <math>D_1</math>, we will use the normal formula: | |||
:::<math>B_{D_1} = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right]</math> | |||
:::<math>B_{D_1} = \frac{\mu_0 \times 20 \times 10}{2} \left[\frac{2(0.13)^2 + (1)^2}{\sqrt{(0.13)^2 + (1)^2}} - 2|0.13| \right]</math> | |||
:::<math>B_{D_1} = 9.62 \times 10^{-5} \text{ T}</math> | |||
::We can now find the net magnetic field at <math>z = 0.13 \text{ m}</math>. Since the up direction has been the positive direction for <math>z</math>, we will use the up direction as the positive direction for the magnetic fields: | |||
:::<math>B_{net} = B_{D_1} - B_{D_2} = 9.62 \times 10^{-5} \text{ T} - 1.5 \times 10^{-4} = - 5.38 \times 10^{-5} \text{ T}</math> | |||
::This means there is a magnetic field with a magnitude of <math>5.38 \times 10^{-5} \text{ T}</math> pointing in the down direction along the axis of rotation of the disks. | |||
==Connectedness== | ==Connectedness== | ||
1. Arago's Rotations utilize the Lorentz force created by a spinning conductive disk. Induction motors are based on Arago's Rotations and are cheaper to produce than | |||
synchronous motors because they do not require permanent magnets. | |||
2. The calculation of the magnetic field produced by a spinning disk requires the use of Calculus, which is a is a large branch of Mathematics. | |||
3. Neodymium disk magnets are used in products that require strong permanent magnets like wind turbines, sensors, speakers, alarms, and more. | |||
==History== | ==History== | ||
The magnetic field produced by a spinning disk was discovered by Francois Arago in 1824. Arago rapidly rotated disks made of conductive material beneath a magnetized needle, and the needle reacted to the magnetic field being produced by the disk. At the time, the phenomenon was difficult to explain. Several scientists investigated Arago's rotations including Joseph Louis Gay-Lussac, Peter Barlow, Charles Babbage, and John Frederick William Herschel. Babbage and Herschel worked together to conduct experiments that tested the phenomenon on different materials, both conductive and non-conductive, and with different sizes of disks and needles. They found that Arago's rotations only worked with a big enough needle and a conductive disk. Later on, Michael Faraday wrote the theory of electromagnetic induction, which explained that Arago's rotations were the product of the disk be an inducted magnet that produced a magnetic field that influenced the magnetic needle above it. | |||
==See also== | ==See also== | ||
| Line 159: | Line 284: | ||
==References== | ==References== | ||
*Matter & Interactions Vol. II | *Matter & Interactions Vol. II | ||
*[https://royalsocietypublishing.org/doi/10.1098/rstl.1825.0023 The Royal Society Volume 115] | |||
*[https://www.sciencedirect.com/topics/engineering/rotating-magnetic-field ScienceDirect] | |||
*[https://aapt.scitation.org/doi/full/10.1119/1.4901191?casa_token=Bg-09Hghc4EAAAAA%3A-I0qc7-QzU2vao3mc8zzY8qaKEDhNG4Hrl5V6S55Mep_oTZjOcqt3sCOL8hPr537dIID-R5cSQ American Journal of Physics, Volume 83, Issue 3] | |||
*[https://www.stanfordmagnets.com/neodymium-magnets.html Stanford Magnets] | |||
Latest revision as of 20:05, 28 November 2021
Claimed by MaKenna Kelly Fall 2021
Main Idea
On this page, we will explore how to solve for the magnetic field produced by a rotating, charged, circular disk.
First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object can produce unique electric fields.
In order to figure out the magnetic field of a disk, we will start from the fundamental principles that we have learned already with regards to how magnetic fields are produced. We will then build on that and include the geometry of the object in question, in this a circular disk, in order to solve for the magnetic field produced by a disk.
Mathematical Model
Say we have a "flat" circular disk with radius [math]\displaystyle{ R }[/math] and carrying a uniform surface charge density [math]\displaystyle{ \sigma }[/math]. It rotates with an angular velocity [math]\displaystyle{ \omega }[/math] about the z-axis.
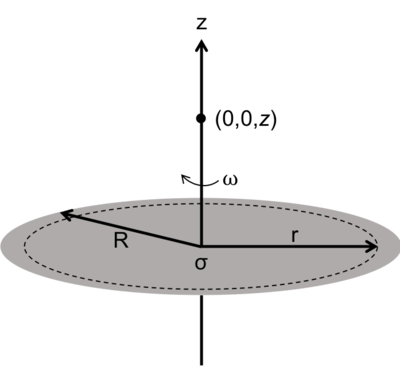
To find the magnetic field [math]\displaystyle{ B }[/math] at any point [math]\displaystyle{ z }[/math] along the rotation axis, we can consider the disk to be a collection of concentric current loops. Breaking the disk into a series of loops with infinitesimal width [math]\displaystyle{ dr }[/math] and with radius [math]\displaystyle{ r }[/math], we will have an infinitesimal area for loop :
- [math]\displaystyle{ dA = 2\pi r dr }[/math], where
- [math]\displaystyle{ A = \pi r^2 }[/math]
And therefore have an infinitesimal charge on each loop of:
- [math]\displaystyle{ dQ = 2\pi \sigma rdr }[/math], where
- [math]\displaystyle{ Q = \sigma A }[/math]
This loop is rotating at an angular velocity [math]\displaystyle{ \omega }[/math], which means the charge [math]\displaystyle{ dQ }[/math] on our loop makes a full rotation around the axis every period,
- [math]\displaystyle{ T = \frac{2\pi}{\omega} }[/math] seconds.
Since a charge [math]\displaystyle{ dQ }[/math] makes a full rotation every [math]\displaystyle{ T }[/math] seconds, our infinitesimally thin ring is a current loop with an infinitesimal current:
- [math]\displaystyle{ dI = \frac{dQ}{T} = \frac{2\pi \sigma rdr}{\frac{2\pi}{\omega}} = \sigma \omega rdr }[/math], where
- [math]\displaystyle{ I = \frac{Q}{t} }[/math]
For this single loop, equivalent to a current [math]\displaystyle{ dI }[/math], we can calculate the field a distance [math]\displaystyle{ z }[/math] above the axis. Using this proof from the Magnetic Field of a Loop page, we can get:
- [math]\displaystyle{ dB = \frac{\mu_0 r^2 dI}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} }[/math]
Now to find the total magnetic field for all of the concentric rings, we must integrate from [math]\displaystyle{ r = 0 }[/math] to [math]\displaystyle{ r = R }[/math]:
- [math]\displaystyle{ B = \int_{0}^{R} \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}} }[/math]
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{0}^{R} }[/math]
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+R^2}{\sqrt{R^2+z^2}} - 2|z| \right] }[/math]
The absolute value around the [math]\displaystyle{ z }[/math] is important because we want the field to be the same on either side of the disk, whether we are in the positive z or negative z direction.
Computational Model
Click the "1" on the right to view and/or edit a computational model of a disk's magnetic field. [1]
Notes about the model:
- the disk is represented by the gray object in the center of the screen
- the arrows represent the magnetic field created by the disk at different observation locations
- the orange arrow represents B1 (magnetic field to the right of the disk)
- the red arrow represents B2 (magnetic field above the disk)
- the green arrow represents B3 (magnetic field to the left of the disk)
- the blue arrow represents B4 (magnetic field below the disk)
Model made by MaKenna Kelly (undergraduate student and an editor of this page)
Examples
Simple
An infinitely thin disk with radius [math]\displaystyle{ R = 2 \text{ m} }[/math] is spinning counter-clockwise at a rate of [math]\displaystyle{ \omega = 15\pi \ \frac{rads}{s} }[/math]. The disk has a uniform charge density [math]\displaystyle{ \rho = 2 \ \frac{C}{A} }[/math]. Imagine the disk is lying flat in the xy-plane.
- a) What is the magnitude and direction of the magnetic field [math]\displaystyle{ 5 \text{ m} }[/math] above the axis of rotation. What about [math]\displaystyle{ 5 \text{ m} }[/math] below the axis of rotation?
- Using a convenient right-hand rule, we curl our fingers in the direction of rotation (AKA the direction of the current). the way our thumb points is the direction of the magnetic field: the (+z) direction.
- To find the magnitude of the magnetic field [math]\displaystyle{ 5 }[/math] meters above the disk, we will call upon our Mathematical Model:
- [math]\displaystyle{ B = \frac{\mu_0 \sigma \omega}{2}\left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math], where in our case
- [math]\displaystyle{ \begin{align} \sigma & = \rho = 2 \\ \omega & = 15\pi \\ R & = 2 \\ z & = 5 \\ \end{align} }[/math]
- We will plug these values in to get:
- [math]\displaystyle{ \begin{align} B & = \frac{\mu_0 \times 2 \times 15\pi}{2}\left[\frac{2(5)^2 + (2)^2}{\sqrt{(5)^2 + (2)^2}} - 2|5| \right] \\ & = \mu_0 \times 15\pi \left[\frac{50 + 4}{\sqrt{25 + 4}} - 10 \right] \\ & = \mu_0 \times 15\pi \left[\frac{54}{\sqrt{29}} - 10 \right] \\ B & = 1.63 \times 10^{-6} \text{ T} \end{align} }[/math]
- Therefore, the rotating, charged disk is creating a magnetic field above the disk pointing "up" with a magnitude of [math]\displaystyle{ 1.63 \times 10^{-6} \text{ T} }[/math].
- To find the direction of the magnetic field below the disk, we once again employ the right-hand rule: our fingers curl in the direction of rotation and we find the magnetic field points in the (+z) direction again.
- To find the magnitude of the magnetic field [math]\displaystyle{ 5 }[/math] meters below the disk, we will use the same formula from above:
- [math]\displaystyle{ B = \frac{\mu_0 \sigma \omega}{2}\left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math], where in our case:
- [math]\displaystyle{ \begin{align} \sigma & = \rho = 2 \\ \omega & = 15\pi \\ R & = 2 \\ z & = -5 \\ \end{align} }[/math]
- We will plug these values in to get:
- [math]\displaystyle{ \begin{align} B & = \frac{\mu_0 \times 2 \times 15\pi}{2}\left[\frac{2(-5)^2 + (2)^2}{\sqrt{(-5)^2 + (2)^2}} - 2|-5| \right] \\ & = \mu_0 \times 15\pi \left[\frac{50 + 4}{\sqrt{25 + 4}} - 10 \right] \\ & = \mu_0 \times 15\pi \left[\frac{54}{\sqrt{29}} - 10 \right] \\ B & = 1.63 \times 10^{-6} \text{ T} \end{align} }[/math]
- Therefore, the rotating, charged disk is creating a magnetic field below the disk pointing "up" with a magnitude of [math]\displaystyle{ 1.63 \times 10^{-6} \text{ T} }[/math].
- Notice the the magnitude and direction of the magnetic field at the two points are equal. This is no coincidence. In general, if [math]\displaystyle{ z_1 = a }[/math] and [math]\displaystyle{ z_2 = -a }[/math], then they will have the same direction and magnitude for the magnetic field (for a rotating disk).
Middling
A uniformly charged disk of radius [math]\displaystyle{ R = 0.01 \ \text{m} }[/math] is rotating at a rate of [math]\displaystyle{ \omega = 2\pi \ \frac{\text{rads}}{s} }[/math] and is losing its charge to its surroundings in such a way that the charge density of the disk is increasing by [math]\displaystyle{ \frac{d \sigma}{dt} = \pi te^{-\frac{5t^2}{\pi}} }[/math], where [math]\displaystyle{ t }[/math] is time in seconds.
- a) What is the magnitude of the magnetic field at time [math]\displaystyle{ t_0 = 0 }[/math] along the axis of rotation, if the charge density is [math]\displaystyle{ 3 \ \frac{C}{A} }[/math] at this time?
- We can immediately use our Mathematical Model to solve for the magnetic field:
- [math]\displaystyle{ B(z) = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math], where
- [math]\displaystyle{ z }[/math] is a point along the axis of rotation
- In our case the following values have been specified for us:
- [math]\displaystyle{ \begin{align} \sigma & = 3 \\ \omega & = 2\pi \\ R & = 0.01 \\ \end{align} }[/math]
- Therefore, we can plug these values in and simplify for an answer:
- [math]\displaystyle{ \begin{align} B(z) & = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] \\ & = \frac{\mu_0 \times 3 \times 2\pi}{2} \left[\frac{2z^2 + (0.01)^2}{\sqrt{z^2 + (0.01)^2}} - 2|z| \right] \\ B(z) & = \left(1.184 \times 10^{-5}\right) \left[\frac{2z^2 + \left(1 \times 10^{-4}\right)}{\sqrt{z^2 + \left(1 \times 10^{-4}\right)}} - 2|z| \right]\\ \end{align} }[/math]
- b) What is the magnetic field at time [math]\displaystyle{ t_f = 10 \ s }[/math] ?
- To find the magnitude of the magnetic field, we will have to find the new charge density, since we were told it is increasing with time. To do this, we will integrate [math]\displaystyle{ \frac{d \sigma}{dt} }[/math] to solve for [math]\displaystyle{ \sigma (t) }[/math]:
- [math]\displaystyle{ \frac{d \sigma}{dt} = \pi te^{-\frac{5t^2}{\pi}} }[/math]
- or:
- [math]\displaystyle{ d \sigma = \left[ \pi te^{-\frac{5t^2}{\pi}} \right] dt }[/math]
- or:
- [math]\displaystyle{ \int d \sigma = \int \pi te^{-\frac{5t^2}{\pi}} \ dt }[/math]
- or:
- [math]\displaystyle{ \begin{align} \sigma (t) & = \int \pi te^{-\frac{5t^2}{\pi}} \ dt \\ & = \pi \int te^{-\frac{5t^2}{\pi}} \ dt \\ & = \pi \int -\frac{\pi}{10} e^u du \ \text{ where } u = -\frac{5t^2}{\pi} \text{ and } du = -\frac{10}{\pi} t \ dt \\ & = -\frac{\pi^2}{10} \int e^u du \\ & = -\frac{\pi^2}{10} \left[e^u \right] + C\\ \sigma (t) & = -\frac{\pi^2}{10} \left[e^{-\frac{5t^2}{\pi}} \right] + C \\ \end{align} }[/math]
- To find [math]\displaystyle{ C }[/math] we use the original charge density of time [math]\displaystyle{ t_0 = 0 }[/math]:
- [math]\displaystyle{ \sigma (0) = 3 }[/math]
- Therefore:
- [math]\displaystyle{ 3 = -\frac{\pi^2}{10} \left[e^{-\frac{5(0)^2}{\pi}} \right] + C }[/math]
- [math]\displaystyle{ C = 3 + \frac{\pi^2}{10} }[/math]
- This gives [math]\displaystyle{ \sigma (t) }[/math] as:
- [math]\displaystyle{ \begin{align} \sigma (t) & = -\frac{\pi^2}{10} \left[e^{-\frac{5t^2}{\pi}} \right] + 3 + \frac{\pi^2}{10} \\ \sigma (t) & = \frac{\pi^2}{10} \left[1 - e^{-\frac{5t^2}{\pi}} \right] + 3 \\ \end{align} }[/math]
- Now we can find [math]\displaystyle{ \sigma (10) }[/math]:
- [math]\displaystyle{ \sigma (10) = \frac{\pi^2}{10} \left[1 - e^{-\frac{5(10)^2}{\pi}} \right] + 3 }[/math]:
- This gives:
- [math]\displaystyle{ \sigma (10) \approx 4 \ \frac{C}{A} }[/math]
- Now we can find the magnetic field generated by the rotating disk:
- [math]\displaystyle{ B(z) = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math]
- [math]\displaystyle{ B(z) = \left(1.58 \times 10^{-5} \right) \left[\frac{2z^2 + \left(1 \times 10^{-4}\right)}{\sqrt{z^2 + \left(1 \times 10^{-4}\right)}} - 2|z| \right] }[/math]
Difficult
Two concentric infinitely thin disks are touching and rotating in opposite directions in the xy-plane. Disk 1 [math]\displaystyle{ (D_1) }[/math] is the inner disk, with a radius of [math]\displaystyle{ R_1 = 1 \text{ m} }[/math]; it is rotating counter-clockwise at a rate of [math]\displaystyle{ \omega_1 = 10 \ \frac{\text{rads}}{s} }[/math]. Disk 2 [math]\displaystyle{ (D_2) }[/math] is the outer disk, with a radius of [math]\displaystyle{ R_2 = 5 \text{ m} }[/math]; it is rotating clockwise at a rate of [math]\displaystyle{ \omega_2 = 3 \ \frac{\text{rads}}{s} }[/math]. Their charge density is [math]\displaystyle{ \sigma = 20 \ \frac{C}{A} }[/math] See [2] for clarification. Ignore any frictional or electromagnetic effects the disks may have on each other.
- a) What is the direction of the magnetic field created by [math]\displaystyle{ D_1 }[/math] at a point along the axis of rotation and above the disk? What is the direction of the magnetic field created by [math]\displaystyle{ D_2 }[/math] at a point along the axis of rotation and above the disk?
- Using the right-hand rule, we see the two rotating disks are creating opposing magnetic fields; [math]\displaystyle{ D_1 }[/math] creates a field pointing straight up along the axis of rotation. [math]\displaystyle{ D_2 }[/math] creates a magnetic field pointing straight down along the axis of rotation.
- b) What is the magnitude of the net magnetic field [math]\displaystyle{ 0.13 \text{ m} }[/math] along the axis of rotation and above the disks?
- We can answer this question by solving for each magnetic field separately and then summing them (taking their directions into account). The major impediment is that the general formula:
- [math]\displaystyle{ B_z = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math]
- will not work for the outer disk [math]\displaystyle{ D_2 }[/math]. This is because in the derivation, we integrated from [math]\displaystyle{ r = 0 }[/math] to [math]\displaystyle{ r = R }[/math]. For [math]\displaystyle{ D_2 }[/math], we must integrate from [math]\displaystyle{ r = R_1 }[/math] to [math]\displaystyle{ r = R_2 }[/math], since those are its radial bounds. The formula will work as usual for [math]\displaystyle{ D_1 }[/math].
- Going back to the third to last step of the derivation, we have:
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}} }[/math]
- We will correct this for [math]\displaystyle{ D_2 }[/math] by replacing [math]\displaystyle{ r = 0 }[/math] by [math]\displaystyle{ r = R_1 }[/math]:
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \int_{R_1}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}} }[/math]
- Of course the integral will be the same as before, but with different bounds:
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{R_1}^{R} }[/math]
- [math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - \frac{2z^2 + {R_1}^2}{\sqrt{z^2 + {R_1}^2}} \right] }[/math]
- Therefore, the magnetic field created by [math]\displaystyle{ D_2 \ 0.13 \text{ m} }[/math] along the axis of rotation and above the disks is:
- [math]\displaystyle{ B_{D_2} = \frac{\mu_0 \times 20 \times 3}{2} \left[\frac{2(0.13)^2 + (5)^2}{\sqrt{(0.13)^2 + (5)^2}} - \frac{2(0.13)^2 + (1)^2}{\sqrt{(0.13)^2 + (1)^2}} \right] }[/math]
- [math]\displaystyle{ B_{D_2} = 1.5 \times 10^{-4} \text{ T} }[/math]
- To find the magnetic field due to [math]\displaystyle{ D_1 }[/math], we will use the normal formula:
- [math]\displaystyle{ B_{D_1} = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math]
- [math]\displaystyle{ B_{D_1} = \frac{\mu_0 \times 20 \times 10}{2} \left[\frac{2(0.13)^2 + (1)^2}{\sqrt{(0.13)^2 + (1)^2}} - 2|0.13| \right] }[/math]
- [math]\displaystyle{ B_{D_1} = 9.62 \times 10^{-5} \text{ T} }[/math]
- We can now find the net magnetic field at [math]\displaystyle{ z = 0.13 \text{ m} }[/math]. Since the up direction has been the positive direction for [math]\displaystyle{ z }[/math], we will use the up direction as the positive direction for the magnetic fields:
- [math]\displaystyle{ B_{net} = B_{D_1} - B_{D_2} = 9.62 \times 10^{-5} \text{ T} - 1.5 \times 10^{-4} = - 5.38 \times 10^{-5} \text{ T} }[/math]
- This means there is a magnetic field with a magnitude of [math]\displaystyle{ 5.38 \times 10^{-5} \text{ T} }[/math] pointing in the down direction along the axis of rotation of the disks.
Connectedness
1. Arago's Rotations utilize the Lorentz force created by a spinning conductive disk. Induction motors are based on Arago's Rotations and are cheaper to produce than synchronous motors because they do not require permanent magnets.
2. The calculation of the magnetic field produced by a spinning disk requires the use of Calculus, which is a is a large branch of Mathematics.
3. Neodymium disk magnets are used in products that require strong permanent magnets like wind turbines, sensors, speakers, alarms, and more.
History
The magnetic field produced by a spinning disk was discovered by Francois Arago in 1824. Arago rapidly rotated disks made of conductive material beneath a magnetized needle, and the needle reacted to the magnetic field being produced by the disk. At the time, the phenomenon was difficult to explain. Several scientists investigated Arago's rotations including Joseph Louis Gay-Lussac, Peter Barlow, Charles Babbage, and John Frederick William Herschel. Babbage and Herschel worked together to conduct experiments that tested the phenomenon on different materials, both conductive and non-conductive, and with different sizes of disks and needles. They found that Arago's rotations only worked with a big enough needle and a conductive disk. Later on, Michael Faraday wrote the theory of electromagnetic induction, which explained that Arago's rotations were the product of the disk be an inducted magnet that produced a magnetic field that influenced the magnetic needle above it.
See also
Further reading
- Matter & Interactions Vol. II
- Magnetic Fields of Spinning Disk and Sphere
External links
- Magnetic Field of a Long Straight Wire
- Magnetic Field of a Loop
- Biot-Savart Law
- Biot-Savart Law for Currents
- Current
References
- Matter & Interactions Vol. II
- The Royal Society Volume 115
- ScienceDirect
- American Journal of Physics, Volume 83, Issue 3
- Stanford Magnets
