Hooke’s Law: Difference between revisions
No edit summary |
|||
| (33 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Vinutna Veeragandham | Author: Vinutna Veeragandham | ||
| Line 6: | Line 6: | ||
==The Main Idea== | ==The Main Idea== | ||
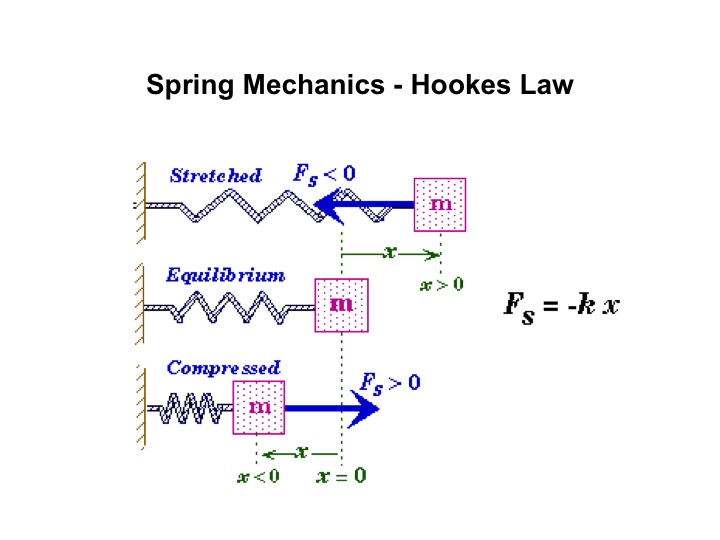
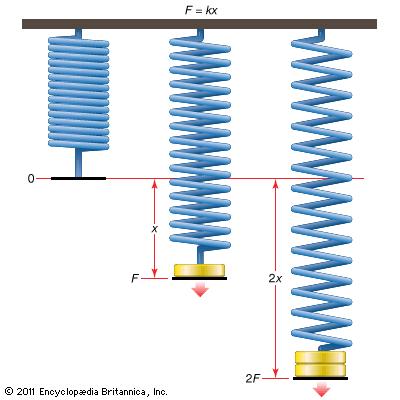
Hooke's Law demonstrates the relationship between forces applied to a spring and elasticity. It states that the force needed to extend or compress a spring by some distance is proportional to that distance. This law applies to many different materials such as balloons or strings; an elastic body to which Hooke's law applies is known as linear-elastic. Hooke's Law has been the basis for the modern Theory of Elasticity, led to creation of new inventions as well as been the foundation of many different branches of science such as seismology, molecular mechanics and acoustics. | Hooke's Law demonstrates the relationship between forces applied to a spring and elasticity. It states that the force needed to extend or compress a spring by some distance is proportional to that distance. This law applies to many different materials such as balloons or strings; an elastic body to which Hooke's law applies is known as linear-elastic. Hooke's Law has been the basis for the modern Theory of Elasticity, led to creation of new inventions as well as been the foundation of many different branches of science such as seismology, molecular mechanics and acoustics. | ||
[[File:146782-004-1CD38EA0.jpg]] | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
| Line 16: | Line 18: | ||
''X'' - spring displacement from the spring's free end while at equilibrium position, SI Units: Newtons/Meters | ''X'' - spring displacement from the spring's free end while at equilibrium position, SI Units: Newtons/Meters | ||
[[File:Slide31.jpg]] | |||
===A Computational Model=== | ===A Computational Model=== | ||
| Line 21: | Line 26: | ||
A computational representation of Hooke's Law can be created using VPython. The code below puts Hooke's law in action. | A computational representation of Hooke's Law can be created using VPython. The code below puts Hooke's law in action. | ||
# GlowScript 1.1 VPython | |||
L0=.1 #the natural length of the spring | L0=.1 #the natural length of the spring | ||
| Line 87: | Line 92: | ||
X = total stretch distance | X = total stretch distance | ||
F = applied force | F = applied force | ||
Find X... | Find X... | ||
X = F/k | X = F/k | ||
F = kx = mg | F = kx = mg | ||
| Line 95: | Line 100: | ||
k = [ (0.15) * (9.8) ] / 0.046 | k = [ (0.15) * (9.8) ] / 0.046 | ||
k = 32 N/m | k = 32 N/m | ||
With both masses... | With both masses... | ||
X = [ (m + M) * g ] / k | X = [ (m + M) * g ] / k | ||
X = [ (0.15 + 0.50) * (9.8) ] / 32 | X = [ (0.15 + 0.50) * (9.8) ] / 32 | ||
| Line 102: | Line 108: | ||
===Difficult=== | ===Difficult=== | ||
A mass of 1.0kg is attached to a spring obeying Hooke's Law F = k*s, where F is the force applied and s the spring extension. The spring constant, k is 50 N/m. The spring and the object lie on a surface tilted 45 degrees with respect to the vertical. Neglect friction. Answer the following questions: | |||
a. What is the extension of the spring? | |||
b. What is the work done by gravity in extending the spring by the above extension? | |||
a) | |||
1kg = 9.8 N | |||
Resolve the force into horizontal component... | |||
9.8 * sin(45) = 6.93 | |||
F = k*s --> F/k = s | |||
s = 6.93/50 = 0.139 m | |||
b) | |||
Work done by gravity can be calculated by calculating the change in potential energy. | |||
U = (1/2) * k * (x^2) | |||
= (1/2) * 50 * (0.139^2) | |||
= 0.483 J | |||
==Connectedness== | ==Connectedness== | ||
Hooke's law is relevant in our everyday lives from small objects all the way to massive structures. We can see the simplest of applications of Hooke's law in rubber bands, scrunchies and even our clothes. Just as Hooke's law prescribes we can see that there is a limit to which they can be stretched and still restore their original shape; after this limit, they will break or lose their shape. Larger applications of Hooke's law can be seen in the newer constructions of overpasses, which are high level road bridges. In specific, the tendons that create tension in order to suspend the bridge during construction follow design specifications based on Hooke's law. Even the skyscrapers and other tall buildings that we find ourselves in everyday include Hooke's law as a vital part of their design process. With different types of weather such as earthquakes or hurricanes, there is a possibility for huge forces to push on the buildings. The materials and geometry of the building are the factors in the stiffness of the building. The relationship between this stiffness and the force that pressures the building is summarized by Hooke's law, and in order to stay within it's limitations so the building doesn't collapse, architects must keep the law in mind during construction. Hooke's law holds a great importance in our lives whether or not we realize it. | |||
==History== | ==History== | ||
Hooke's law was discovered by 17th century scientist Robert Hooke. Hooke was a British physicist who actually discovered this law in 1660 when he was working on designs for the springs of a clock. Originally, Hooke announced his discovery as "Ut tensio, sic vis" which is Latin for "As the extension, so the force," and this later became known as Hooke's law. | |||
==See Also== | |||
===Further Reading=== | |||
Spring Force [http://www.physicsbook.gatech.edu/Spring_Force] | |||
Simple Harmonic Motion [http://www.physicsbook.gatech.edu/Simple_Harmonic_Motion] | |||
Work [http://www.physicsbook.gatech.edu/Work] | |||
===External Links=== | |||
Khan Academy [https://www.khanacademy.org/science/physics/work-and-energy/hookes-law/v/intro-to-springs-and-hooke-s-law] | |||
Spring/Hooke's Law Simulation [http://phet.colorado.edu/sims/mass-spring-lab/mass-spring-lab_en.html] | |||
==References== | |||
Universe Today [http://www.universetoday.com/55027/hookes-law/] | |||
Hyper Physics [http://hyperphysics.phy-astr.gsu.edu/hbase/permot2.html] | |||
Latest revision as of 22:56, 12 April 2016
Author: Vinutna Veeragandham
Hooke's Law: the force needed to extend or compress a spring by some distance is proportional to that distance.
The Main Idea
Hooke's Law demonstrates the relationship between forces applied to a spring and elasticity. It states that the force needed to extend or compress a spring by some distance is proportional to that distance. This law applies to many different materials such as balloons or strings; an elastic body to which Hooke's law applies is known as linear-elastic. Hooke's Law has been the basis for the modern Theory of Elasticity, led to creation of new inventions as well as been the foundation of many different branches of science such as seismology, molecular mechanics and acoustics.
A Mathematical Model
F = -kX
F - restoring force, force by which the free end of the spring is being pulled, SI Units: Newtons
k - spring constant, an inherent property of the string, SI Units: Meters
X - spring displacement from the spring's free end while at equilibrium position, SI Units: Newtons/Meters
A Computational Model
A computational representation of Hooke's Law can be created using VPython. The code below puts Hooke's law in action.
# GlowScript 1.1 VPython L0=.1 #the natural length of the spring k=15 #spring constant #the holder is the top plate for the spring holder= box(pos=vec(-.1,.1,0), size=vec(.1,.005,.1)) #the ball and the spring should be obvious #note that the ball has a trail ball=sphere(pos=vec(-.1,-L0+.1,0), radius=0.02, color=color.red, make_trail=true) spring=helix(pos=holder.pos, axis=ball.pos-holder.pos, radius=.02, coils=10) ball.m=0.1 #mass of the ball in kg ball.p=ball.m*vec(0,0,0) #starting momentum mass times velocity dr=vec(0,-0.05,0) #this is the displacement of the spring ball.pos=ball.pos+dr g=vec(0,-9.8,0) #gravitational field t=0 dt=0.01 #size of the time step #putting the loop as "while True" means it runs forever #you could change this to while t< 10: or something while t<3: rate(100) #this says 100 calculations per second #L is the length of the spring, from the holder to the ball L=ball.pos-holder.pos #remember that mag(R) gives the magnitude of vector R #remember that norm(R) gives the unit vector for R Fs=-k*(mag(L)-L0)*norm(L) #this is Hooke's law #this calculates the net force F=Fs+ball.m*g #update the momentum ball.p=ball.p+F*dt #update the position of the ball ball.pos= ball.pos +ball.p*dt/ball.m #this next line updates the spring spring.axis=ball.pos-holder.pos
Examples
Simple
A spring has a spring constant that is equal to 3.5. What force will make it stretch 4 cm?
F = k * x F = 3.5 * 4 F = 14 kg
Middling
A 0.15 kg mass is attached to a vertical spring and hangs at rest a distance of 4.6 cm below its original position. An additional 0.50 Kg mass is then suspended from the first mass and the system is allowed to descend to a new equilibrium position. What is the total extension of the spring?
m = 0.15 kg M = 0.5 kg x = 4.6 cm X = total stretch distance F = applied force Find X... X = F/k F = kx = mg k = mg/x k = [ (0.15) * (9.8) ] / 0.046 k = 32 N/m With both masses... X = [ (m + M) * g ] / k X = [ (0.15 + 0.50) * (9.8) ] / 32 X = 0.20 m
Difficult
A mass of 1.0kg is attached to a spring obeying Hooke's Law F = k*s, where F is the force applied and s the spring extension. The spring constant, k is 50 N/m. The spring and the object lie on a surface tilted 45 degrees with respect to the vertical. Neglect friction. Answer the following questions:
a. What is the extension of the spring?
b. What is the work done by gravity in extending the spring by the above extension?
a) 1kg = 9.8 N Resolve the force into horizontal component... 9.8 * sin(45) = 6.93 F = k*s --> F/k = s s = 6.93/50 = 0.139 m
b) Work done by gravity can be calculated by calculating the change in potential energy. U = (1/2) * k * (x^2) = (1/2) * 50 * (0.139^2) = 0.483 J
Connectedness
Hooke's law is relevant in our everyday lives from small objects all the way to massive structures. We can see the simplest of applications of Hooke's law in rubber bands, scrunchies and even our clothes. Just as Hooke's law prescribes we can see that there is a limit to which they can be stretched and still restore their original shape; after this limit, they will break or lose their shape. Larger applications of Hooke's law can be seen in the newer constructions of overpasses, which are high level road bridges. In specific, the tendons that create tension in order to suspend the bridge during construction follow design specifications based on Hooke's law. Even the skyscrapers and other tall buildings that we find ourselves in everyday include Hooke's law as a vital part of their design process. With different types of weather such as earthquakes or hurricanes, there is a possibility for huge forces to push on the buildings. The materials and geometry of the building are the factors in the stiffness of the building. The relationship between this stiffness and the force that pressures the building is summarized by Hooke's law, and in order to stay within it's limitations so the building doesn't collapse, architects must keep the law in mind during construction. Hooke's law holds a great importance in our lives whether or not we realize it.
History
Hooke's law was discovered by 17th century scientist Robert Hooke. Hooke was a British physicist who actually discovered this law in 1660 when he was working on designs for the springs of a clock. Originally, Hooke announced his discovery as "Ut tensio, sic vis" which is Latin for "As the extension, so the force," and this later became known as Hooke's law.
See Also
Further Reading
Spring Force [1]
Simple Harmonic Motion [2]
Work [3]
External Links
Khan Academy [4]
Spring/Hooke's Law Simulation [5]
References
Universe Today [6]
Hyper Physics [7]