Combining Electric and Magnetic Forces: Difference between revisions

Latest revision as of 01:13, 25 November 2018

Claimed by Luis Pimentel Fall 2018 Edited the Velocity Selector section. Went into more detail about why this works and created a VPython trinket demonstrating and visualizing a velocity selector for particles.

Though the pattern in which electric and magnetic forces interact with particles is observably different, their effects can be quantitatively be compared. The principle of adding the two functions of force as a net force is one that now serves as a fundamental principle of electromagnetics. It serves as a building block for many important Laws such as Hall Effect and Motional Emf.

The Main Idea

If a charged particle within an electric field is moving in a magnetic field, the particle is subject to an Electric Force and a Magnetic Force. The net force on the particle is called the Lorentz Force, which is the sum of electric and magnetic forces.

A Mathematical Model

Electric Forces

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 1. An electric force acts in a pattern parallel to the electric field, pointing radially inward or outward of a particle. The direction depends on the signs of the interacting charged particles.

• A particle being acted upon by an electric force will move in a straight line, in the path, or negative path depending on charge, of the the electric field line (See Figure 1) .

• Electric fields point in a direction radially outward/ inward of a charged particle. There are four possible scenarios for the interaction of 2 charged particles:

1. A negatively charged particle (p1) is acting on a negatively charged particle (p2)

- p2 feels force pointing radially outward from p2

2. A positively charged particle (p1) is acting on a negatively charged particle (p2)

- p2 feels force pointing radially inward toward p2

3. A negatively charged particle (p1) is acting on a positively charged particle (p2)

- p2 feels force pointing radially inward toward p1

4. A positively charged particle (p1) is acting on a positively charged particle (p2)

- p2 feels force pointing radially outward from p1

• The electric force formula: [math]\displaystyle{ \vec {F}_{E}=q\vec E }[/math]

- Force on the observed particle is determined by the interaction of the charge of the observed particle and the electric field created by other charged particles.

Magnetic Forces

**Figure 2.** Magnetic Fields follow a helical pattern

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 3. Magnetic Force Right Hand Rule

• The magnetic force on a charged particle is orthogonal to the magnetic field.

• The particle must be moving with some velocity for a magnetic force to be present.

• Particles move perpendicular to the magnetic field lines in a helical manner (See Figure 2)

• To find the magnetic force, you can use the Right Hand Rule as follows (See Figure 3):

1. Thumb in direction of the velocity

2. Fingers in the direction of the magnetic field

3. Your palm will face in the direction of the Magnetic Force

• The magnetic force formula: [math]\displaystyle{ {\vec {F}_{M} = q\vec {v}\times\vec {B}} }[/math]

- q is the charge of the moving charge, including its sign

- [math]\displaystyle{ \vec v }[/math] is the velocity of the moving charge

- [math]\displaystyle{ \vec B }[/math] is the applied magnetic field, in Tesla

- Note: if [math]\displaystyle{ \vec v }[/math] and [math]\displaystyle{ \vec B }[/math] are parallel to each other, [math]\displaystyle{ {\vec {F}_{M} = 0} }[/math] ([math]\displaystyle{ {\vec {A}\times\vec {B} = |\vec A||\vec B|sin(θ) = 0} }[/math])

Electric and Magnetic Forces Combined

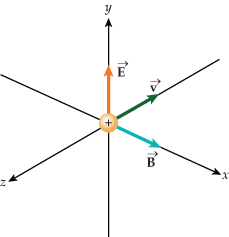
**Figure 4.** The electric field, magnetic field, and velocity vector are all perpendicular to each other

• The Lorentz Force formula:

[math]\displaystyle{ {\vec {F}_{net} = \vec {F}_{E} + \vec {F}_{M}} }[/math]

[math]\displaystyle{ {\vec {F}_{net} = q\vec E + q\vec {v}\times\vec {B}} }[/math]

• When the net force is equal to zero, the velocity stays constant.

[math]\displaystyle{ {\vec {F}_{E} = \vec {F}_{M}} }[/math]

[math]\displaystyle{ {q\vec E = q\vec {v}\times\vec {B}} }[/math]

As seen in Figure 4 , when the net forces acting on a particle are balanced the electric field, magnetic field, and velocity vector are all perpendicular to each other. The electric and magnetic forces are equal but opposite. When forces are not balanced the trajectory of the the particle will change.

The Lorentz Force calculation is now a fundamental principle of electromagnetism.

A Computational Model

Following are diagrams which display a uniform electric field in the +x direction and a uniform magnetic field in +y direction for a proton and an electron, with varying velocities.

The force equations and the right hand rule can both be used to determine the directions of the forces:

- According to [math]\displaystyle{ {\vec {F}_{E} = q\vec E} }[/math], [math]\displaystyle{ {\vec {F}_{Eproton}} }[/math] points in the direction of [math]\displaystyle{ \vec E }[/math] and [math]\displaystyle{ {\vec {F}_{Eelectron}} }[/math] points in opposite direction of [math]\displaystyle{ \vec E }[/math].

- According to [math]\displaystyle{ {\vec {F}_{M} = q\vec {v}\times\vec {B}} }[/math], [math]\displaystyle{ \vec {F}_{M} = 0 }[/math] when [math]\displaystyle{ \vec v }[/math] is parallel to [math]\displaystyle{ \vec B }[/math]. The direction of [math]\displaystyle{ \vec {F}_{M} }[/math] can be determined by the cross multiplication of [math]\displaystyle{ \vec v }[/math] and [math]\displaystyle{ \vec B }[/math] and by the sign of [math]\displaystyle{ q }[/math].

• Proton at rest:

- Direction of electric force: +x

- Direction of magnetic force: no magnetic force

• Proton moving in +x direction:

- Direction of electric force: +x

- Direction of magnetic force: +z

• Proton moving in +y direction:

- Direction of electric force: +x

- Direction of magnetic force: no magnetic force

• Proton moving in +z direction:

- Direction of electric force: +x

- Direction of magnetic force: -x

• Electron at rest:

- Direction of electric force: -x

- Direction of magnetic force: no magnetic force

• Electron moving in +x direction:

- Direction of electric force:-x

- Direction of magnetic force: -z

• Electron moving in +y direction:

- Direction of electric force: -x

- Direction of magnetic force: no magnetic force

• Electron moving in +z direction:

- Direction of electric force: -x

- Direction of magnetic force: +x

Examples

Simple

A proton is moving with velocity 7e8 in the +x direction. The trajectory of the proton is constant. There is an electric field in the area of 3.6e7 in the +y direction. Calculate the direction and magnitude of the magnetic field acting on the particle?

Solution:

Step 1: [math]\displaystyle{ {|q\vec E| = |q\vec v\vec B|} }[/math]

Step 2: [math]\displaystyle{ {\vec {E} = \vec {v}\vec {B}} }[/math]

Step 3: [math]\displaystyle{ {\vec {B} = \frac {\vec {E}} {\vec {v}} = \frac {3.6e7} {7e8}} }[/math]

Answer: [math]\displaystyle{ {\vec {B} = 0.051 T} }[/math]

The magnetic field is in the +z direction.

Middling

At a particular instant, a proton is moving with velocity <0,5e5,0> m/s and an electron is moving with velocity <-4.2e2,0,0> m/s. The electron is located 1.4e-3 m below the proton (in the -y direction). Determine the net force on the electron due to the proton.

Solution:

Step 1: [math]\displaystyle{ {\vec {F}_{net} = \vec {F}_{E} + \vec {F}_{B}} }[/math]

Step 2: [math]\displaystyle{ {\vec {F}_{net} = \vec {F}_{E} + 0 = q\vec {E}} }[/math] (At the electron's location, [math]\displaystyle{ \vec B = 0 }[/math] because the velocity of the proton is parallel to [math]\displaystyle{ \hat{r} }[/math])

Step 3: [math]\displaystyle{ {\vec {E} = \frac {1} {4πεo} \frac {q} {r^2} \hat{r}} }[/math] ([math]\displaystyle{ \hat{r} = \lt 0,-1,0\gt and r = 1.4e-3 m }[/math])

Step 4: [math]\displaystyle{ \vec E = \lt 0,-7.35e-4,0\gt N/C }[/math]

Step 5: [math]\displaystyle{ {\vec {F}_{net} = -e \vec E = \lt 0,1.18e-22,0\gt N} }[/math]

Difficult

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 5. Middle example diagram.

A copper bar of length L and zero resistance slides at a constant velocity, v. There is a uniform magnetic field, B, directed into the page. A voltmeter is connected across a resistor, R, and reads ΔV. See Figure 5. Determine the direction of the magnetic force on the diagram and the current through the resistor. Your answer should be in terms of the given variables.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 6. Middle example solution.

Solution:

Step 1: Direction of the Magnetic Force - Use right hand rule or [math]\displaystyle{ {\vec v \times\vec B} }[/math]. See Figure 6.

Step 2: Current through the resistor -

[math]\displaystyle{ {ΔV}_{round trip} = 0 }[/math]

[math]\displaystyle{ {{ΔV}_{round trip} + motional emf - {ΔV}_{resistor} = 0} }[/math]

[math]\displaystyle{ motional emf = IR }[/math]

[math]\displaystyle{ I = \frac {motional emf} {R} }[/math]

[math]\displaystyle{ {|q\vec E| = |q\vec v\vec B|} }[/math], [math]\displaystyle{ {|ΔV| = IR} }[/math]

[math]\displaystyle{ {qE = qvB} }[/math]

[math]\displaystyle{ E = vB }[/math]

[math]\displaystyle{ motional emf = |ΔV| = E*ΔL = vBL }[/math]

[math]\displaystyle{ {I = \frac {vBL} {R}} }[/math]

Connectedness

The Lorentz Force principle has been a component in many modern day inventions and critical building block for many physics principles. With known forces, we can predict the very important figure, the velocity and trajectory of a moving particle.

Applications

Velocity Selector

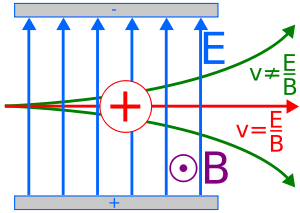
The Velocity Selector is a device used to filter particles based on their velocity. A Velocity Selector uses controlled, perpendicular, electric and magnetic fields to filter certain charged particles (See Figure 7 ). These electric and magnetic fields exert a Lorentz force on the particle. For the particle to remain unaffected, the Lorentz force must be zero. Therefore, we have:

[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} = 0 }[/math]

[math]\displaystyle{ \lvert q\vec{E}\rvert = \lvert q\vec{v} ⨯ \vec{B}\rvert }[/math]

[math]\displaystyle{ qE= qvB }[/math]

[math]\displaystyle{ v = E/B }[/math]

From this relationship we can adjust to our electric and magnetic fields to pass particles with a desired speed of a narrow band through a target area. Particles at a desired speed will remain unaffected while other particles with undesired speeds will be deflected. This technique is used in technologies such as electron microscopes and spectrometers.

The following VPython trinket module is a demonstration of a velocity selector. Two particles of different speeds pass through an area with perpendicular magnetic and electric fields. Within this trinket, you can change the initial values of the velocity selector and particle velocities to see how this affects the particles' motion as they try to pass through a circular area.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 7.1. SImulation of a Velocity Selector

Velocity Selector Trinket

Electric Motor

An electric motor is a device that uses the Lorentz force to convert electric energy into mechanical energy. Using the magnetic torque principle, electric energy is created by using the magnetic field of a magnet. The torque laws are based off the principles of the net electric and magnetic forces.

History

The relationship between electric and magnetic forces was first questioned in the mid-18th century when Johann Tobias Mayer (1760) and Henry Cavendish (1762) proposed that the force on magnetic poles and electrically charged objects followed the inverse-square law, which was proven to be true by Charles-Augustin in 1784.

Following Michael Faraday's proposal of the concept of electric and magnetic fields, James Clerk Maxwell was first to mathematically prove the concepts. In 1865, Maxwell's field equations consisted of some form of the Lorentz force equation, but at the time it was not clear how it related to forces on charged moving particles. J.J Thomson was the first to attempt a derivation of Maxwell's field equations, and he derived a basic form of the formula for the electromagnetic forces on a charged moving particle in relation to the properties of the particle and its external fields. In 1892, Hendrik Lorentz corrected mistakes of the old formula and derived the modern form of the equation, which contains the forces due to both electric and magnetic fields.

All images found on google image search: https://en.wikipedia.org/wiki/Magnetic_field https://en.wikipedia.org/wiki/Wien_filter http://aplusphysics.com/wordpress/regents/em/electric-field/

Fields

@@ Line 1: / Line 1: @@
-Claimed by Alana Kaplan (Fall, 2015); Claimed to Edit by Alexis Jacob (Spring, 2016 - ''Added middle and difficult examples, figures, and minor format changes'')
+Claimed by Luis Pimentel Fall 2018
-Claimed by Ha Eun An (Fall 2016)
+Edited the Velocity Selector section. Went into more detail about why this works and created a VPython trinket demonstrating and visualizing a velocity selector for particles.
 Though the pattern in which electric and magnetic forces interact with particles is observably different, their effects can be quantitatively be compared. The principle of adding the two functions of force as a net force is one that now serves as a fundamental principle of electromagnetics. It serves as a building block for many important Laws such as [[Hall Effect]] and  [[Motional Emf]].
@@ Line 47: / Line 47: @@
 :3. Your palm will face in the direction of the Magnetic Force
-• The magnetic force on an object is: <math>\vec {F}_{M}=q\vec v x \vec B </math>
+• The magnetic force formula: <math> {\vec {F}_{M} = q\vec {v}\times\vec {B}} </math>
-Note that if the velocity and magnetic field are parallel the magnetic force is zero; this is due to AxB = |A||B|sin(θ). If the angle between the two vectors is 0 or 180 degrees (parallel), then sin(θ) = 0. Therefore, AxB = 0.
+:- q is the charge of the moving charge, including its sign
+:- <math>\vec v</math> is the velocity of the moving charge
+:- <math>\vec B</math> is the applied magnetic field, in Tesla
+:- Note: if <math>\vec v</math> and <math>\vec B</math> are parallel to each other, <math> {\vec {F}_{M} = 0} </math> (<math> {\vec {A}\times\vec {B} = |\vec A||\vec B|sin(θ) = 0} </math>)
 ====Electric and Magnetic Forces Combined====
 [[File:Velocity selector.gif|thumb| '''Figure 4.''' The electric field, magnetic field, and velocity vector are all perpendicular to each other  ]]
-The net force acting on a particle passing through a magnetic and electric field is:
-::[[File:Fnet.jpg]]
+• The Lorentz Force formula:
-This net force calculation is known as "Lorentz Force"
+:<math> {\vec {F}_{net} = \vec {F}_{E} + \vec {F}_{M}} </math>
+:<math> {\vec {F}_{net} = q\vec E + q\vec {v}\times\vec {B}} </math>
-When the net force is equal to zero, the velocity stays constant. The net force is equal when:
+• When the net force is equal to zero, the velocity stays constant.
+:<math> {\vec {F}_{E} = \vec {F}_{M}} </math>
-[[File:Force=0.jpg]]
+:<math> {q\vec E = q\vec {v}\times\vec {B}} </math>
 As seen in '''Figure 4''' , when the net forces acting on a particle are balanced the electric field, magnetic field, and velocity vector are all perpendicular to each other. The electric and magnetic forces are equal but opposite. When forces are not balanced the trajectory of the the particle will change.
@@ Line 65: / Line 68: @@
 The Lorentz Force calculation is now a fundamental principle of electromagnetism.
-==Examples==
+===A Computational Model===
-===Simple===
+Following are diagrams which display a uniform electric field in the +x direction and a uniform magnetic field in +y direction for a proton and an electron, with varying velocities.
-'''Q:''' A proton is moving with velocity 7e8 in the +x direction. The trajectory of the proton is constant. There is an electric field in the area of 3.6e7 in the +y direction. Calculate the direction and magnitude of the magnetic field acting on the particle?
+The force equations and the right hand rule can both be used to determine the directions of the forces:
+:- According to <math> {\vec {F}_{E} = q\vec E} </math>, <math> {\vec {F}_{Eproton}} </math> points in the direction of <math> \vec E </math> and <math> {\vec {F}_{Eelectron}} </math> points in opposite direction of <math> \vec E </math>.
+:- According to <math> {\vec {F}_{M} = q\vec {v}\times\vec {B}} </math>, <math> \vec {F}_{M} = 0 </math> when <math> \vec v </math> is parallel to <math> \vec B </math>. The direction of <math> \vec {F}_{M} </math> can be determined by the cross multiplication of <math> \vec v </math> and <math> \vec B </math> and by the sign of <math> q </math>.
-'''A:''' |qE| = |qvB|
+• '''Proton at rest:'''
+:[[File:protonr2.png]]
+:- Direction of electric force: +x
+:- Direction of magnetic force: no magnetic force
-E = vB
-B = E/v = 3.6e7/7e8
+• '''Proton moving in +x direction:'''
+:[[File:protonx2.png]]
+:- Direction of electric force: +x
+:- Direction of magnetic force: +z
-B = 0.051 T
-The magnetic field is in the +z direction.
+• '''Proton moving in +y direction:'''
+:[[File:protony.png]]
+:- Direction of electric force: +x
+:- Direction of magnetic force: no magnetic force
-===Middling===
-'''Q:''' At a particular instant, a proton is moving with velocity <0,5e5,0> m/s and an electron is moving with velocity <-4.2e2,0,0> m/s. The electron is located 1.4e-3 m below the proton (in the -y direction).
-Determine the net force on the electron due to the proton.
+• '''Proton moving in +z direction:'''
+:[[File:protonz.png]]
+:- Direction of electric force: +x
+:- Direction of magnetic force: -x
-'''A:''' Fnet = F(e) + F(B)
+• '''Electron at rest:'''
+:[[File:electronr2.png]]
+:- Direction of electric force: -x
+:- Direction of magnetic force: no magnetic force
-@ the electron's location, B = 0 because the velocity of the proton is parallel to r-hat.
-Fnet = F(e) + 0 = q*E
+• '''Electron moving in +x direction:'''
+:[[File:electronx.png]]
+:- Direction of electric force:-x
+:- Direction of magnetic force: -z
-E = (1/4πεo)*(q/r^2)*rhat
-where rhat = <0,-1,0> and r = 1.4e-3 m
+• '''Electron moving in +y direction:'''
+:[[File:electrony.png]]
+:- Direction of electric force: -x
+:- Direction of magnetic force: no magnetic force
-E = <0,-7.35e-4,0> N/C
-Fnet = -e*E = <0,1.18e-22,0> N
+• '''Electron moving in +z direction:'''
+:[[File:electronz.png]]
+:- Direction of electric force: -x
+:- Direction of magnetic force: +x
-===Difficult===
+==Examples==
-[[File:Middle_Example_A.jpg|thumb| '''Figure 5.''' Middle example diagram. ]]
-'''Q:''' A copper bar of length L and zero resistance slides at a constant velocity, v. There is a uniform magnetic field, B, directed into the page. A voltmeter is connected across a resistor, R, and reads ΔV. See '''Figure 5'''.
-Determine the direction of the magnetic force on the diagram and the current through the resistor. Your answer should be in terms of the given variables.
+===Simple===
-[[File:Middle_Example_B.jpg|thumb| '''Figure 6.''' Middle example solution. ]]
+A proton is moving with velocity 7e8 in the +x direction. The trajectory of the proton is constant. There is an electric field in the area of 3.6e7 in the +y direction. Calculate the direction and magnitude of the magnetic field acting on the particle?
-'''A:''' ''Direction of the Magnetic Force''- Use right hand rule for v cross B. See '''Figure 6'''.
-''Current through the resistor''-
+:''Solution:''
+:Step 1: <math> {|q\vec E| = |q\vec v\vec B|} </math>
+:Step 2: <math> {\vec {E} = \vec {v}\vec {B}} </math>
+:Step 3: <math> {\vec {B} = \frac {\vec {E}} {\vec {v}} = \frac {3.6e7} {7e8}} </math>
-ΔV round trip = 0
+:Answer: <math> {\vec {B} = 0.051 T} </math>
-ΔV round trip = +motional emf - ΔV resistor = 0
+The magnetic field is in the +z direction.
-motional emf = IR
+===Middling===
-I = (motional emf/R)
+At a particular instant, a proton is moving with velocity <0,5e5,0> m/s and an electron is moving with velocity <-4.2e2,0,0> m/s. The electron is located 1.4e-3 m below the proton (in the -y direction). Determine the net force on the electron due to the proton.
+:''Solution:''
+:Step 1: <math> {\vec {F}_{net} = \vec {F}_{E} + \vec {F}_{B}} </math>
+:Step 2: <math> {\vec {F}_{net} = \vec {F}_{E} + 0 = q\vec {E}} </math> (At the electron's location, <math> \vec B = 0 </math> because the velocity of the proton is parallel to <math> \hat{r} </math>)
+:Step 3: <math> {\vec {E} = \frac {1} {4πεo} \frac {q} {r^2} \hat{r}} </math> (<math> \hat{r} = <0,-1,0> and r = 1.4e-3 m</math>)
+:Step 4: <math> \vec E = <0,-7.35e-4,0> N/C </math>
+:Step 5: <math> {\vec {F}_{net} = -e \vec E = <0,1.18e-22,0> N} </math>
-According to Lorentz force, |F(e)| = |F(B)|
+===Difficult===
+[[File:Middle_Example_A.jpg|thumb| '''Figure 5.''' Middle example diagram. ]]
-q*E = q*v*B
+A copper bar of length L and zero resistance slides at a constant velocity, v. There is a uniform magnetic field, B, directed into the page. A voltmeter is connected across a resistor, R, and reads ΔV. See '''Figure 5'''. Determine the direction of the magnetic force on the diagram and the current through the resistor. Your answer should be in terms of the given variables.
-E = v*B
+[[File:Middle_Example_B.jpg|thumb| '''Figure 6.''' Middle example solution. ]]
-|ΔV| = E*ΔL = vBL
+:''Solution:''
+:Step 1: Direction of the Magnetic Force - Use right hand rule or <math> {\vec v \times\vec B} </math>. See '''Figure 6'''.
-I = (vBL)/R
+:Step 2: Current through the resistor -
+::: <math> {ΔV}_{round trip} = 0 </math>
+::: <math> {{ΔV}_{round trip} + motional emf - {ΔV}_{resistor} = 0} </math>
+::: <math> motional emf = IR </math>
+::: <math> I = \frac {motional emf} {R} </math>
+::: <math> {|q\vec E| = |q\vec v\vec B|} </math>, <math> {|ΔV| = IR} </math>
+::: <math> {qE = qvB} </math>
+::: <math> E = vB </math>
+::: <math> motional emf = |ΔV| = E*ΔL = vBL </math>
+::: <math> {I = \frac {vBL} {R}} </math>
 ==Connectedness==
@@ Line 143: / Line 180: @@
 [[File:Velocityselector2.png|thumb| '''Figure 7.''' Illustration of a Velocity Selector ]]
-The Velocity Selector is a device used to filter particles based on their velocity. A Velocity Selector uses controlled, perpendicular, electric and magnetic fields to filter certain charged particles (See '''Figure 7''' ).  Particles with the correct speed will be unaffected while other particles will be deflected. This technique is used in technologies such as electron microscopes and spectrometers.
+The Velocity Selector is a device used to filter particles based on their velocity. A Velocity Selector uses controlled, perpendicular, electric and magnetic fields to filter certain charged particles (See '''Figure 7''' ). These electric and magnetic fields exert a Lorentz force on the particle. For the particle to remain unaffected, the Lorentz force must be zero. Therefore, we have:
+<math> \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} = 0 </math>
+<math> \lvert q\vec{E}\rvert = \lvert q\vec{v} ⨯ \vec{B}\rvert </math>
+<math> qE= qvB </math>
+<math> v = E/B </math>
+From this relationship we can adjust to our electric and magnetic fields to pass particles with a desired speed of a narrow band through a target area. Particles at a desired speed will remain unaffected while other particles with undesired speeds will be deflected. This technique is used in technologies such as electron microscopes and spectrometers.
+The following VPython trinket module is a demonstration of a velocity selector. Two particles of different speeds pass through an area with perpendicular magnetic and electric fields. Within this trinket, you can change the initial values of the velocity selector and particle velocities to see how this affects the particles' motion as they try to pass through a circular area.
+[[File:velocitySelector3Stages.jpg|thumb| '''Figure 7.1.''' SImulation of a Velocity Selector ]]
+[https://trinket.io/glowscript/d3067081b7 Velocity Selector Trinket]
 '''''Electric Motor'''''
@@ Line 164: / Line 220: @@
 [[Inductance]]
+==History==
+The relationship between electric and magnetic forces was first questioned in the mid-18th century when Johann Tobias Mayer (1760) and Henry Cavendish (1762) proposed that the force on magnetic poles and electrically charged objects followed the inverse-square law, which was proven to be true by Charles-Augustin in 1784.
+Following Michael Faraday's proposal of the concept of electric and magnetic fields, James Clerk Maxwell was first to mathematically prove the concepts. In 1865, Maxwell's field equations consisted of some form of the Lorentz force equation, but at the time it was not clear how it related to forces on charged moving particles. J.J Thomson was the first to attempt a derivation of Maxwell's field equations, and he derived a basic form of the formula for the electromagnetic forces on a charged moving particle in relation to the properties of the particle and its external fields. In 1892, Hendrik Lorentz corrected mistakes of the old formula and derived the modern form of the equation, which contains the forces due to both electric and magnetic fields.
 == See also ==

Combining Electric and Magnetic Forces: Difference between revisions

Latest revision as of 01:13, 25 November 2018

Contents

The Main Idea

A Mathematical Model

Electric Forces

Magnetic Forces

Electric and Magnetic Forces Combined

A Computational Model

Examples

Simple

Middling

Difficult

Connectedness

Applications

Other related topics

History

See also

Further reading

External links

References

Navigation menu