Power (Mechanical): Difference between revisions
(→Simple) |
|||
| Line 154: | Line 154: | ||
The transmission of mechanical power has evolved over the course of the past few centuries. In the 16th century, mechanical power transmission involved systems of push-rods that linked pumps to water wheels. This example is seen further in the late 18th century in German towns where power is transmitted from water wheels to salt wells. This "primitive" is still present in today's day and age, as oil fields transmitting power from pumping engines to pump jacks follow the same principle. Other mediums to transfer mechanical power include hydraulic systems, pneumatic systems, and solid structures such as gears and driveshafts. | The transmission of mechanical power has evolved over the course of the past few centuries. In the 16th century, mechanical power transmission involved systems of push-rods that linked pumps to water wheels. This example is seen further in the late 18th century in German towns where power is transmitted from water wheels to salt wells. This "primitive" is still present in today's day and age, as oil fields transmitting power from pumping engines to pump jacks follow the same principle. Other mediums to transfer mechanical power include hydraulic systems, pneumatic systems, and solid structures such as gears and driveshafts. | ||
== See also == | == See also == | ||
Latest revision as of 20:03, 18 April 2018
EDITING CLAIMED BY TYLER ARNOLD (SPRING 2018)
The Main Idea
Power is the rate of doing work or the amount of energy consumed over an interval of time. In the context of mechanical systems, mechanical power is an aggregation of both forces and movement. Specifically, power is an object's velocity multiplied by the object's force. This accounts for the distance per time. In the context of a shaft, power is calculated as the product of a shaft's torque with its angular velocity. The SI unit for power is watts (J/s).
A Mathematical Model
Below are the types of mathematical equations and calculations that are associated with power:
When a force is applied over a distance in a unit of time, power is calculated by
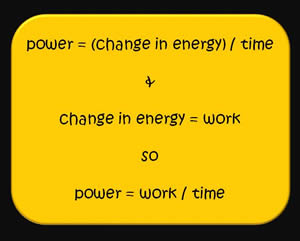
- [math]\displaystyle{ power = \frac{F \Delta r}{\Delta t} = \frac{W}{\Delta t} }[/math]
where F is force, Δr is displacement, Δt is the duration of time and W is work.
It then follows that instantaneous power is
- [math]\displaystyle{ power = F\cdot v }[/math]
where v is velocity.
In rotational systems, power is the product of the torque τ and Angular Velocity ω,
- [math]\displaystyle{ power = \boldsymbol{\tau} \cdot \boldsymbol{\omega}, \, }[/math]
where ω is measured in radians per second. The [math]\displaystyle{ \cdot }[/math] represents scalar product.
The work done by a certain force that moves along a curve can be calculated through the following integral:
- [math]\displaystyle{ W_c = \int_c F * v dt }[/math]
If a force is conservative (meaning that it holds the property where the work done in moving a particle from two locations is independent of the path it takes), we can derive the following formula after applying the gradient theorem:
- [math]\displaystyle{ W_c = U(B) - U(A) }[/math]
Where A and B represent the final and initial locations of along the path in which the work was done.
In the case where we assume that the mechanical system has no losses, we can draw the conclusion that the input power must equal the output power. Knowing this provides us a formula for mechanical advantage, which is a metric for the factor in which a force is amplified through a tool:
- [math]\displaystyle{ P = F_B v_B=F_A v_A }[/math]
With P being the input force, where [math]\displaystyle{ F_A }[/math] is a force that moves with velocity [math]\displaystyle{ v_A }[/math] and [math]\displaystyle{ F_B }[/math] is a force that moves with velocity [math]\displaystyle{ v_B }[/math]. Given these conditions, we can arrive to the mechanical advantage:
- [math]\displaystyle{ MA=\frac{F_A}{F_B}=\frac{v_A}{v_B} }[/math]
Examples
Simple
A certain motor is capable of doing 3000 J of work in 12 s. What is the power output of this motor?
- [math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{3000 J}{12 s} = 250 J/s }[/math]
A weightlifter does 5000 J of work over a time span of 5 seconds. How much power does the weightlifter exert?
- [math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{5000 J}{5 s} = 1000 J/s }[/math]
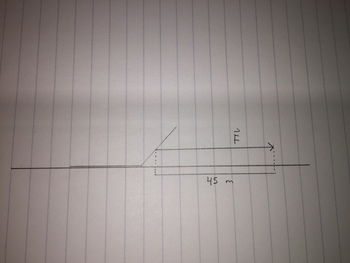
It takes a husky 30 s to pull a sled 45 m. Over that time the dig uses a constant force of 50 N. How much power does the husky exert?
- [math]\displaystyle{ power = \frac{{F}{\Delta r}}{\Delta t} = \frac{{50 N} \cdot {45 m}}{30 s} = \frac{2250 J}{30 s} = 75 J/s }[/math]
Simpler problems will more often than not provide you with the Work, or only require a small calculation to find it.
Middling
Here are questions dealing with human power. (a) If you follow a diet of 2000 food calories per day (2000 kC), what is your average rate of energy consumption in watts (power input)? (A food or “large” calorie is a unit of energy equal to 4.2 J; a regular or “small” calorie is equal to 4200 J.) (b) How many days of a diet of 2000 large calories are equivalent to the gravitational energy change from sea level to the top of Mount Everest, 8848 m above sea level? Assume your weight is 58 kg. (The body is not anywhere near 100% efficient in converting chemical energy into change in altitude. Also note that this is in addition to your basal metabolism.)
(a) [math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{2000 kC}{day} \cdot \frac{4200 J}{1 kC} \cdot \frac{1 day}{24 h} \cdot \frac{1 h}{3600 s} = 97.2 J/s }[/math]
(b) [math]\displaystyle{ {\frac{97.2 J}{s}} \cdot \frac{3600 s}{1 h} \cdot \frac{24 h}{1 day} = 8398080 J/day }[/math]
- [math]\displaystyle{ \Delta U_g = mg\Delta y = (58 kg)(9.8 m/s^2)(8848 m - 0 m) = 5029203.2 J }[/math]
- [math]\displaystyle{ \Delta t = \frac{W}{power} = \frac{5029203.2 J}{8398080 J/day} = 0.599 days }[/math]
A man starting at rest accelerates in the positive x direction. It has a mass of 1.1 x 103 kg and has a constant acceleration of 4.6m/s2 for 5 seconds. Determine in the average power generated by this vehicle:
- [math]\displaystyle{ V_o = 0 m/s   m=1,100kg   a=4.6m/s^2   t=5s }[/math]
- [math]\displaystyle{ P={\frac{W}{t}}   W=F*S   W=\Delta KE }[/math]
- [math]\displaystyle{ x=V_ot+{\frac{1}{2}}at }[/math]
- [math]\displaystyle{ x=0+{\frac{1}{2}}(4.6)*(5)^2 }[/math]
- [math]\displaystyle{ x=57.5m }[/math]
- [math]\displaystyle{ W = mas }[/math]
- [math]\displaystyle{ W = (1,100)*(4.6)*(57.5) }[/math]
- [math]\displaystyle{ W = 290950J }[/math]
- [math]\displaystyle{ P = {\frac{290950}{5}} }[/math]
- [math]\displaystyle{ P = 58190W }[/math]
Intermediate problems usually require a step beyond just finding Work and relating it to time. Power can also be compared to other topics in the physics realm.
Difficult
A bicyclist is going up an inclined slope with an angle [math]\displaystyle{ \alpha }[/math] = 2.9 degrees by a uniform speed of 27 km/h. The magnitude of the air resistance force is given by [math]\displaystyle{ F_{odp} = kv^2 }[/math] kgs/m where the numerical value of [math]\displaystyle{ k = 0.3 }[/math] if the unit of the speed is m/s and the unit of the resistance force is the newton (N). The mass of the bicyclist including the bike is 70 kg. Do not consider the rolling resistance. (a) What forward force exerted on the bike by the road is needed to make the bicyclist move with constant speed? (b) How much work does the bicyclist do when riding a distance of 1200 m? (c) What is the power of the bicyclist during the ride? Assume there is no loss of mechanical energy.
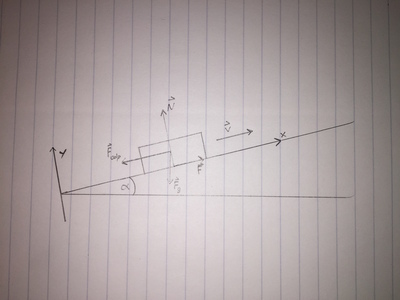
- [math]\displaystyle{ F_g }[/math] = weight
- N = normal force exerted on the bike by the road
- [math]\displaystyle{ F_{odp} }[/math] = air resistance
- F = unknown forward force exerted on the bike by the road
(a) [math]\displaystyle{ x-components: -F_gsin\alpha -F_{odp} + F = 0 }[/math]
- [math]\displaystyle{ y-components: N -F_gcos\alpha = 0 }[/math]
- [math]\displaystyle{ F = F_gsin\alpha + F_{odp} = mgsin\alpha + kv^2 }[/math]
- [math]\displaystyle{ v = \frac{27 km}{h} \cdot \frac{1000 m}{1 km} \cdot \frac{1 h}{3600 s} = 7.5 m/s }[/math]
- [math]\displaystyle{ F = (70 kg)(9.8 m/s^2)sin2.9 + (0.3 kgs/m)(7.5 m/s)^2 = 51.6 N }[/math]
(b) [math]\displaystyle{ W = F\Delta r = (51.6 N)(1200 m) = 61920 J }[/math]
(c) [math]\displaystyle{ power = F\cdot v = (51.6 N)(7.5 m/s) = 387 J/s }[/math]
Difficult problems will require a multitude of forces to be found before calculating the work. These can be tricky so make sure to draw a free body diagram.
Connectedness
1. How is this topic connected to something that you are interested in?
Power is the culmination of many previous concepts we have, such as work and displacement, which is information that can be found using kinematics in certain situations. Power is the concept that is most directly related to my life whether playing a sport and knowing the right about of force to use or helping a friend move into their new home. In a subject that has many abstract, impersonal concepts, power is one that can be recognized and applied to daily life.
2. How is it connected to your major?
Physics applies to more than just engineering science majors. As a biology student with a pre-med concentration, topics on a more personal level connect to biological processes. Working in the field of medicine requires to have an understand of the physiology of the body and how it can be used in order to maximize effectiveness of rehabilitation and repair measures.
3. Is there an interesting industrial application?
Power can be applied to a number of industries. In the medical world, an understanding of power can be utilized to design better prosthetics that allow for people to live better lives after traumatic instances. Instead of just producing a stale replica of an arm, bionics can be created to make the new prosthetic more powerful than the original, biological design.
History
Electrical power transmission has replaced mechanical power transmission in all but the very shortest distances. From the 16th century through the industrial revolution to the end of the 19th century mechanical power transmission was the norm. The oldest long-distance power transmission technology involved systems of push-rods connecting waterwheels to distant mine-drainage and brine-well pumps. The unit of power, the watt, was named after the mechanical engineer James Watt, for his contributions to the development of the steam engine. We can observe this concept of power in our every day life through a measure of horsepower, comparing to the power of a horse.
The transmission of mechanical power has evolved over the course of the past few centuries. In the 16th century, mechanical power transmission involved systems of push-rods that linked pumps to water wheels. This example is seen further in the late 18th century in German towns where power is transmitted from water wheels to salt wells. This "primitive" is still present in today's day and age, as oil fields transmitting power from pumping engines to pump jacks follow the same principle. Other mediums to transfer mechanical power include hydraulic systems, pneumatic systems, and solid structures such as gears and driveshafts.
See also
Further reading
Chabay, Ruth W.; Sherwood, Bruce A. Matter and Interactions, 4th Edition: 1-2. Wiley. Section 7.6.
External links
<http://www.physicsclassroom.com/class/energy/Lesson-1/Power>
<http://hyperphysics.phy-astr.gsu.edu/hbase/pow.html>
References
Chabay, Ruth W.; Sherwood, Bruce A. Matter and Interactions, 4th Edition: 1-2. Wiley.
"General Mechanics/Work and Power." - Wikibooks, Open Books for an Open World. Web. General Mechanics/Work and Power
<https://physicstasks.eu/280/bicyclist-going-uphill>.
<https://en.wikipedia.org/wiki/Power_(physics)>.
<https://en.wikipedia.org/wiki/Power_transmission#Mechanical_power>
<https://en.wikibooks.org/wiki/General_Mechanics/Work_and_Power>