Power (Mechanical)

EDITING CLAIMED BY KAMESH DARISIPUDI (SPRING 2017)

The Main Idea

Power is the rate of doing work or the amount of energy consumed over an interval of time. In the context of mechanical systems, mechanical power is an aggregation of both forces and movement. Specifically, power is an object's velocity multiplied by the object's force. In the context of a shaft, power is calculated as the product of a shaft's torque with its angular velocity. The SI unit for power is watts (J/s)

A Mathematical Model

When a force is applied over a distance in a unit of time, power is calculated by

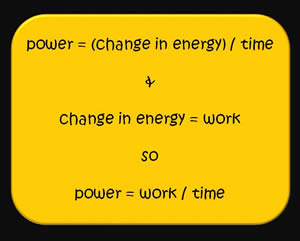
[math]\displaystyle{ power = \frac{F \Delta r}{\Delta t} = \frac{W}{\Delta t} }[/math]

where F is force, Δr is displacement, Δt is the duration of time and W is work.

It then follows that instantaneous power is

[math]\displaystyle{ power = F\cdot v }[/math]

where v is velocity.

In rotational systems, power is the product of the torque τ and Angular Velocity ω,

[math]\displaystyle{ power = \boldsymbol{\tau} \cdot \boldsymbol{\omega}, \, }[/math]

where ω is measured in radians per second. The [math]\displaystyle{ \cdot }[/math] represents scalar product.

The work done by a certain force that moves along a curve can be calculated through the following integral:

[math]\displaystyle{ W_c = \int_c F * v dt }[/math]

If a force is conservative (meaning that it holds the property where the work done in moving a particle from two locations is independent of the path it takes), we can derive the following formula after applying the gradient theorem:

[math]\displaystyle{ W_c = U(B) - U(A) }[/math]

Where A and B represent the final and initial locations of along the path in which the work was done.

In the case where we assume that the mechanical system has no losses, we can draw the conclusion that the input power must equal the output power. Knowing this provides us a formula for mechanical advantage, which is a metric for the factor in which a force is amplified through a tool:

[math]\displaystyle{ P = F_B v_B=F_A v_A }[/math]

With P being the input force, where [math]\displaystyle{ F_A }[/math] is a force that moves with velocity [math]\displaystyle{ v_A }[/math] and [math]\displaystyle{ F_B }[/math] is a force that moves with velocity [math]\displaystyle{ v_B }[/math]. Given these conditions, we can arrive to the mechanical advantage:

[math]\displaystyle{ MA=\frac{F_A}{F_B}=\frac{v_A}{v_B} }[/math]

Examples

Simple

A certain motor is capable of doing 3000 J of work in 12 s What is the power output of this motor?

[math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{3000 J}{12 s} = 250 J/s }[/math]

Middling

Here are questions dealing with human power. (a) If you follow a diet of 2000 food calories per day (2000 kC), what is your average rate of energy consumption in watts (power input)? (A food or “large” calorie is a unit of energy equal to 4.2 J; a regular or “small” calorie is equal to 4200 J.) (b) How many days of a diet of 2000 large calories are equivalent to the gravitational energy change from sea level to the top of Mount Everest, 8848 m above sea level? Assume your weight is 58 kg. (The body is not anywhere near 100% efficient in converting chemical energy into change in altitude. Also note that this is in addition to your basal metabolism.)

(a) [math]\displaystyle{ power = \frac{W}{\Delta t} = \frac{2000 kC}{day} \cdot \frac{4200 J}{1 kC} \cdot \frac{1 day}{24 h} \cdot \frac{1 h}{3600 s} = 97.2 J/s }[/math]

(b) [math]\displaystyle{ {\frac{97.2 J}{s}} \cdot \frac{3600 s}{1 h} \cdot \frac{24 h}{1 day} = 8398080 J/day }[/math]

[math]\displaystyle{ \Delta U_g = mg\Delta y = (58 kg)(9.8 m/s^2)(8848 m - 0 m) = 5029203.2 J }[/math]

[math]\displaystyle{ \Delta t = \frac{W}{power} = \frac{5029203.2 J}{8398080 J/day} = 0.599 days }[/math]

A man starting at rest accelerates in the positive x direction. It has a mass of 1.1 x 10³ kg and has a constant acceleration of 4.6m/s² for 5 seconds. Determine in the average power generated by this vehicle:

[math]\displaystyle{ V_o = 0 m/s   m=1,100kg   a=4.6m/s^2   t=5s }[/math]

[math]\displaystyle{ P={\frac{W}{t}}   W=F*S   W=\Delta KE }[/math]

[math]\displaystyle{ x=V_ot+{\frac{1}{2}}at }[/math]

[math]\displaystyle{ x=0+{\frac{1}{2}}(4.6)*(5)^2 }[/math]

[math]\displaystyle{ x=57.5m }[/math]

[math]\displaystyle{ W = mas }[/math]

[math]\displaystyle{ W = (1,100)*(4.6)*(57.5) }[/math]

[math]\displaystyle{ W = 290950J }[/math]

[math]\displaystyle{ P = {\frac{290950}{5}} }[/math]

[math]\displaystyle{ P = 58190W }[/math]

Difficult

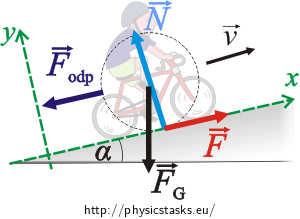
A bicyclist is going up an inclined slope with an angle [math]\displaystyle{ \alpha }[/math] = 2.9 degrees by a uniform speed of 27 km/h. The magnitude of the air resistance force is given by [math]\displaystyle{ F_{odp} = kv^2 }[/math] kgs/m where the numerical value of [math]\displaystyle{ k = 0.3 }[/math] if the unit of the speed is m/s and the unit of the resistance force is the newton (N). The mass of the bicyclist including the bike is 70 kg. Do not consider the rolling resistance. (a) What forward force exerted on the bike by the road is needed to make the bicyclist move with constant speed? (b) How much work does the bicyclist do when riding a distance of 1200 m? (c) What is the power of the bicyclist during the ride? Assume there is no loss of mechanical energy.

[math]\displaystyle{ F_g }[/math] = weight

N = normal force exerted on the bike by the road

[math]\displaystyle{ F_{odp} }[/math] = air resistance

F = unknown forward force exerted on the bike by the road

(a) [math]\displaystyle{ x-components: -F_gsin\alpha -F_{odp} + F = 0 }[/math]

[math]\displaystyle{ y-components: N -F_gcos\alpha = 0 }[/math]

[math]\displaystyle{ F = F_gsin\alpha + F_{odp} = mgsin\alpha + kv^2 }[/math]

[math]\displaystyle{ v = \frac{27 km}{h} \cdot \frac{1000 m}{1 km} \cdot \frac{1 h}{3600 s} = 7.5 m/s }[/math]

[math]\displaystyle{ F = (70 kg)(9.8 m/s^2)sin2.9 + (0.3 kgs/m)(7.5 m/s)^2 = 51.6 N }[/math]

(b) [math]\displaystyle{ W = F\Delta r = (51.6 N)(1200 m) = 61920 J }[/math]

(c) [math]\displaystyle{ power = F\cdot v = (51.6 N)(7.5 m/s) = 387 J/s }[/math]

Connectedness

1. How is this topic connected to something that you are interested in?

I've always been fascinated with the evolution of power generation over time as society itself evolves. As a result, I have been interested in the ways power is stored, generated, and applied.

2. How is it connected to your major?

My major of industrial and systems engineering deals with making systems efficient and as optimized as possible. With mechanical power applied in the context of industrial engineering, we can approach and address questions pertaining to the efficient transfer of power within mechanical systems.

3. Is there an interesting industrial application?

An interesting application of mechanical power is seen in hydraulic systems where hydroelectric generators, canals, and other power generations facilities use water to pump and push, consequently storing and transferring mechanical energy.

History

Electrical power transmission has replaced mechanical power transmission in all but the very shortest distances. From the 16th century through the industrial revolution to the end of the 19th century mechanical power transmission was the norm. The oldest long-distance power transmission technology involved systems of push-rods connecting waterwheels to distant mine-drainage and brine-well pumps. The unit of power, the watt, was named after the mechanical engineer James Watt, for his contributions to the development of the steam engine. We can observe this concept of power in our every day life through a measure of horsepower, comparing to the power of a horse.

The transmission of mechanical power has evolved over the course of the past few centuries. In the 16th century, mechanical power transmission involved systems of push-rods that linked pumps to water wheels. This example is seen further in the late 18th century in German towns where power is transmitted from water wheels to salt wells. This "primitive" is still present in today's day and age, as oil fields transmitting power from pumping engines to pump jacks follow the same principle. Other mediums to transfer mechanical power include hydraulic systems, pneumatic systems, and solid structures such as gears and driveshafts.

See also

• Work
• Gravitational Potential Energy
• Newton's Second Law of Motion
• System & Surroundings

Further reading

Chabay, Ruth W.; Sherwood, Bruce A. Matter and Interactions, 4th Edition: 1-2. Wiley. Section 7.6.

External links

<http://www.physicsclassroom.com/class/energy/Lesson-1/Power>
<http://hyperphysics.phy-astr.gsu.edu/hbase/pow.html>

References

Chabay, Ruth W.; Sherwood, Bruce A. Matter and Interactions, 4th Edition: 1-2. Wiley.
"General Mechanics/Work and Power." - Wikibooks, Open Books for an Open World. Web. General Mechanics/Work and Power
<https://physicstasks.eu/280/bicyclist-going-uphill>.
<https://en.wikipedia.org/wiki/Power_(physics)>.
<https://en.wikipedia.org/wiki/Power_transmission#Mechanical_power>