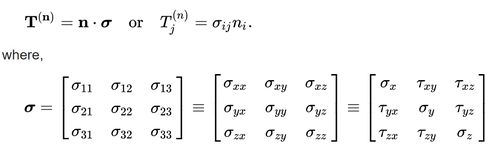Fluid Mechanics: Difference between revisions
No edit summary |
|||
| Line 23: | Line 23: | ||
== Examples: A sampling of equations that could be used in an introductory fluid mechanics class. == | == Examples: A sampling of equations that could be used in an introductory fluid mechanics class. == | ||
'''Navier-Stokes equations''' describe the motion of viscous fluid substances. It is derived as a form of the cauchy momentum equation. (7) | '''Navier-Stokes equations''' describe the motion of viscous fluid substances. It is derived as a form of the cauchy momentum equation. (7) | ||
[[File:Navier stokes.JPG]] | [[File:Navier stokes.JPG|500px]] | ||
*ρ is the density | *ρ is the density | ||
*u is the flow velocity | *u is the flow velocity | ||
| Line 31: | Line 31: | ||
*I is the identity matrix | *I is the identity matrix | ||
*τ is the deviatoric stress tensor | *τ is the deviatoric stress tensor | ||
**[[File:Cauchy stress tensor.JPG]] | **[[File:Cauchy stress tensor.JPG|500px]] | ||
*g represents body accelerations acting on the continuum | *g represents body accelerations acting on the continuum | ||
*⊗ is the outer product that makes the equation u⊗v = uvT true | *⊗ is the outer product that makes the equation u⊗v = uvT true | ||
| Line 37: | Line 37: | ||
---- | ---- | ||
'''Reynolds number flows''' is used to predict flow patterns. (11) The equation is: | '''Reynolds number flows''' is used to predict flow patterns. (11) The equation is: | ||
[[File:Reynolds equation.JPG]] | [[File:Reynolds equation.JPG|500px]] | ||
*ρ is the density of the fluid (SI units: kg/m3) | *ρ is the density of the fluid (SI units: kg/m3) | ||
*u is the velocity of the fluid with respect to the object (m/s) | *u is the velocity of the fluid with respect to the object (m/s) | ||
| Line 60: | Line 60: | ||
**Fluid mechanics is extremely applicable in industries that incorporate hydraulics and hydroelectric power. Both of these, and many other industrial applications, play a huge part in various mechanisms used in daily life. | **Fluid mechanics is extremely applicable in industries that incorporate hydraulics and hydroelectric power. Both of these, and many other industrial applications, play a huge part in various mechanisms used in daily life. | ||
**Georgia Tech also has its own fluid mechanics lab! | **Georgia Tech also has its own fluid mechanics lab! | ||
[[File:Fluid mechanics lab pt 2.JPG]] | [[File:Fluid mechanics lab pt 2.JPG|500px]] | ||
[[File:Fluid mechanics lab.JPG]] | [[File:Fluid mechanics lab.JPG|500px]] | ||
Revision as of 21:20, 16 April 2018
Claimed / Created by Anna Munns Spring 2018
The Main Idea
Fluid mechanics focuses on how fluids (gases or liquids) respond to forces that finds its importance in various fields, specifically hydraulics and many engineering disciplines. (1,2) Water has been historically studied the most out of most fluids, but the field is not limited to water. (1) The field of fluid dynamics consists of: fluid statics, fluid kinematics, and fluid dynamics. Fluid statics is the study of fluids at rest, fluid kinematics is the study of fluids when they are moving (does not include pressure forces), and fluid dynamics is the study of fluids when they are moving while incorporating pressure forces.

Mathematical Model
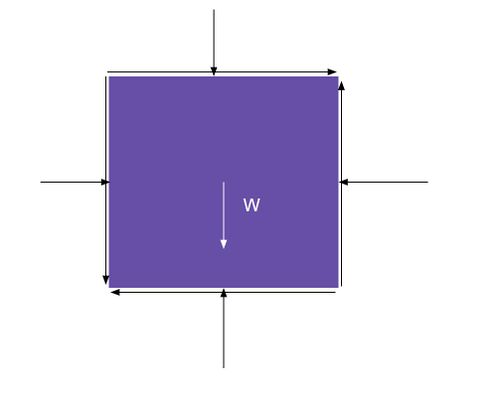
While very complex, many physics principles are applicable to fluid mechanics, namely Newton’s first and second law. Fluid statics utilizes Newton’s first law, an object at rest will stay at rest unless acted upon by an unbalanced force, or Fnet = 0. (4) Fluid mechanics and Fluid dynamics use Newton’s second law which deals with the behavior of objects where existing forces are unbalanced, or Fnet = mass x acceleration. This first picture represents a fluid particle at rest and the second represents a fluid particle in motion.
Computational Model
There is an entire branch of fluid mechanics that is dedicated to computationally modeling fluid dynamics using numerical analysis and data structures. (6) While extremely complex, here are some pictures that have been modeled using computational fluid dynamics.
Examples: A sampling of equations that could be used in an introductory fluid mechanics class.
Navier-Stokes equations describe the motion of viscous fluid substances. It is derived as a form of the cauchy momentum equation. (7)

- ρ is the density
- u is the flow velocity
- ∇∙ is the divergence (8) (the volume density of the outward magnitude and direction of a flow (flux)) (9)
- p is the pressure
- t is time
- I is the identity matrix
- τ is the deviatoric stress tensor
- g represents body accelerations acting on the continuum
- ⊗ is the outer product that makes the equation u⊗v = uvT true
Reynolds number flows is used to predict flow patterns. (11) The equation is:
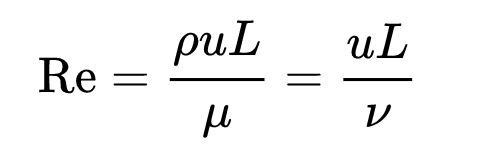
- ρ is the density of the fluid (SI units: kg/m3)
- u is the velocity of the fluid with respect to the object (m/s)
- L is a characteristic linear dimension (defines the length scale of a physical system) (12.) (m)
- μ is the dynamic viscosity of the fluid (Pa·s or N·s/m2 or kg/m·s)
- ν is the kinematic viscosity of the fluid (m2/s).
The Bernoulli Equation is the equation that is used to show that energy is conserved when analyzing fluids. There is a term called the “Bernoulli effect” that is whe fluid pressure lowers in regions where flow velocity has gone up. (13) The basis of the equation is:
- energy/unit initial = energy/unit final
- P1 + ½ ρv12 + ρgh1 = P2 + ½ ρv22 + ρgh2
- P is the pressure energy
- P1 + ½ ρv12 + ρgh1 = P2 + ½ ρv22 + ρgh2
Connectedness
- How is the topic connected to something that I am interested in?
- This topic is very interesting because it has real applications with the human body. The human body is nearly 60% water so fluid mechanics comes into play with other subjects such as biology and together the two fields of study can help with the research involved to fight diseases and save lives. (3)
- How is it connected to my major?
- My major is Industrial Engineering, and while on the surface fluid mechanics has no direct connection to IE, IE is very focused on efficiency and optimization. These two characteristics of IE are primary goals of people who study fluid dynamics: optimizing the use of fluids in the most efficient way possible.
- Is there an interesting industrial application?
- Fluid mechanics is extremely applicable in industries that incorporate hydraulics and hydroelectric power. Both of these, and many other industrial applications, play a huge part in various mechanisms used in daily life.
- Georgia Tech also has its own fluid mechanics lab!
History
The emergence of fluid mechanics as an interest began in around 250 BC when it was founded by Archimedes, a famous mathematician and inventor. Allegedly, Archimedes was taking a bath when suddenly he jumped out of the bath and ran through the streets of Syracuse, Greece screaming “Eureka!” Hydrodynamics was not deeply studied until the 18th century when Leonhard Euler and Daniel Bernoulli explored hydrodynamics, which was more based off of Newton’s dynamic principles. (1.)
References
The references are numbered according to the numbers in parenthesis throughout the page. 1. [1] 2. [2] 3. Pocock, Jennifer. ASEE Prism; Washington Vol. 26, Iss. 2, (Oct 2016): 22. “Fluid Dynamic” 4. [3] 5. [4] 6. [5] 7. [6] 8. [7] 9. [8] 10. [9] 11. [10] 12. [11] 13. [12] 14. [13] 15. [14] 16. [15]