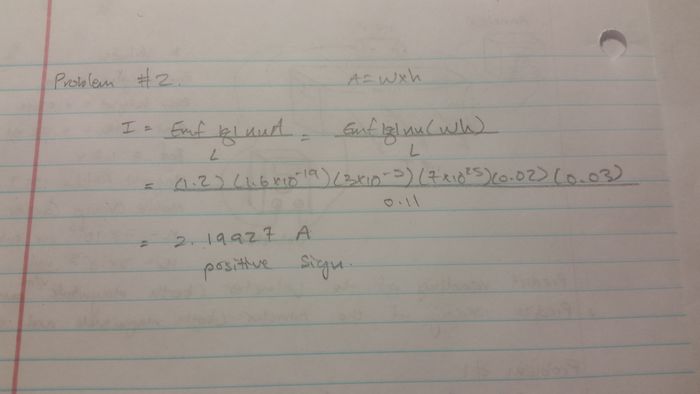Hall Effect

The Hall Effect is the electric polarization of a block or slab of metal that occurs when a current is run through it while it is subject to a magnetic field perpendicular to the current.

The Main Idea

When a mobile charge, either positive or negative, flows through a metal block and is influenced by a magnetic field, the magnetic force on the charges force them to begin concentrating on one side of the block. Thus the block polarizes and has negative charges on one side and positive on the other in order to remain neutral. This grouping of positive charges in one part of the block and negative charges in another part of the block creates an electric field and thus an electric force equal on magnitude to the magnetic force that causes the initial polarization, but opposite in direction. The magnetic and electric forces cancel each other out and after some time, the charges flow normally through the block and do not group on one side or the other of the block. This perpendicular electric field also creates a potential difference known as the "Hall Voltage."

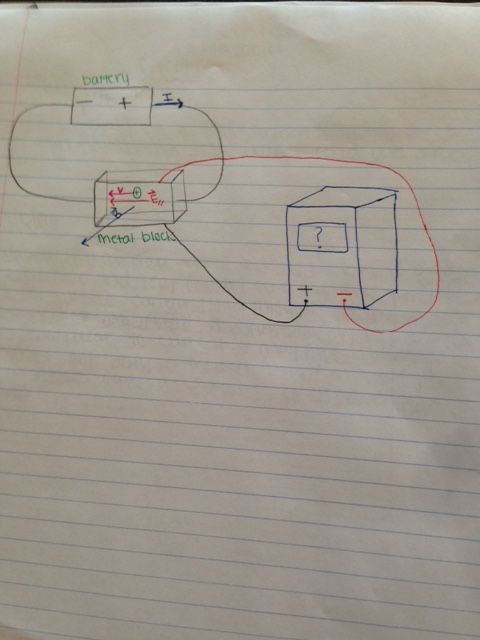
Part 1: Normal circuit (No Magnetic Field Yet)

(For simplicity, the mobile charges in this example have already been determined to be negatively charged electrons. This will not always be the case and it should not be assumed that the mobile charges are electrons)

Mobile electrons flow through a wire due to a parallel electric field inside the wire. This electric field is caused by an energy source, most commonly a battery. The parallel electric field flows from an area of high potential (i.e. the positive end of the battery) to an area of low potential (i.e. the negative end of the battery). This is the same direction as the conventional current. Since electrons are negatively charged, they flow in the opposite direction of the parallel electric field.

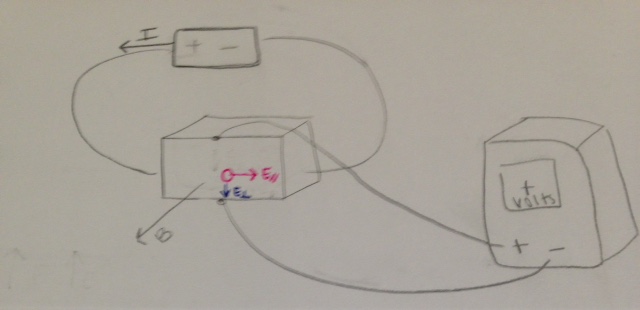
Part 2: Initial Transient State (Magnetic Field Present)

Mobile electrons are subjected to a magnetic field perpendicular to their motion as they flow through the wire. This results in the mobile charges being forced onto one side of the block by the magnetic force. This grouping of mobile charges on one side of the block creates an electric force. As time passes, more mobile charges are deposited on the side of the block and the electric force increases in magnitude.

Part 3: Steady State (Magnetic Field Still Present, but abated)

Over time massive quantities of charges are concentrated on one side of the block. As the charges build up, they will begin to create a charged area on one surface of the conductor. The charged surface will create an electric force to oppose the magnetic force that is pushing new electrons onto this charged surface. This opposing electric force is called the transverse electric force. When enough mobile charges have collected, their combined transverse electric force will be equal in magnitude to the magnetic force that is holding them. At this point, there is no net vertical force pushing more electrons against the surface of the conductor and these electrons will flow normally again, as they would if there was no magnetic field present. This is called the steady state.

A Mathematical Model

Part 1: Normal circuit (No Magnetic Field Yet)

[math]\displaystyle{ F_{electric, parallel} = qE_{parallel} }[/math]

Where q is the electric charge of the mobile charge. As F and E are vectors, a negative charge results in an electric force in the opposite direction of the electric field.

Part 2: Initial Transient State (Magnetic Field Present)

[math]\displaystyle{ F_{magnetic} = q(v\; Χ \;B) }[/math]

Where v is the velocity of the mobile charge and B is the magnetic field. For help calculating the cross product, including an example using the Hall Effect, see Right-Hand_Rule. REMEMBER, the mobile charge will move in the opposite direction of the cross product if it is negative, similar to how it behaves in an electric field.

Part 3: Steady State (Magnetic Field Still Present, but abated)

[math]\displaystyle{ F_{electric, perpendicular} = qE_{perpendicular} }[/math]

[math]\displaystyle{ |F_{electric, perpendicular}| = |F_{magnetic}| }[/math]

Computational Model

In this diagram, it is assumed the charge carrier is a negatively charged electron.

Examples

The following are 3 examples that help to reinforce the concepts of the Hall Effect and two examples that involves actual calculation. Make sure to understand the conceptual examples before doing the examples with calculation because many of the calculation require the application of these concepts into the problem.

Conceptual Examples

Here are the 3 conceptual examples regarding the Hall Effect. They are categorized in level of difficulty.

Simple

Question: A metal slab is connected to a battery by two wires. Conventional current flows clockwise and the mobile charge in the block is positive. The block also experiences a magnetic field out of the page. The slab is also connected to a voltmeter.The positive end of the voltmeter is connected to the bottom of the block and the negative end of the voltmeter is connected to the top of the block. See attached photo for a diagram.

Click for Solution

In order to determine this, we must determine what direction the magnetic force is. In this case, since magnetic force is qv X B, the magnetic force points up. This means that the mobile charges (positive) will be pushed towards the top of the block and the negative charge will be at the bottom of the block, so that the block will remain neutrally charged. Remember: a voltmeter will have a positive reading if the positive end is connected to the part with the larger potential. In this case, the larger potential is at the top because that is where the positive charge is, but the negative end of the voltmeter is connected there. The voltmeter will have a negative reading.

Middling

Question: A battery and metal block are connected by 2 wires. Conventional current flows counterclockwise. A voltmeter is attached to the block with its positive lead at the top of the block and its negative lead at the bottom of the block. The voltmeter has a positive reading. What sign does the mobile charge have? (See attached diagram)

Click for Solution

First of all, due to the Voltmeter having a positive reading, we know that the electric field perpendicular (or the electric field that the Voltmeter is telling us about) points from where the positive lead of the voltmeter is connected to the negative lead (in this example, from top to bottom). We also know that Fmagnetic + Felectric_perpendicular equals zero, so F_b and F_e must have opposite signs. F_b is calculated using I*dl X B. The right hand rule tells us that F_b points in the positive y direction. This tells us that F_e perpendicular must point in the negative y direction. F_e is simply (E*q). As determined earlier, E already points in - y direction so we can conclude that the mobile charges are positive.

Difficult

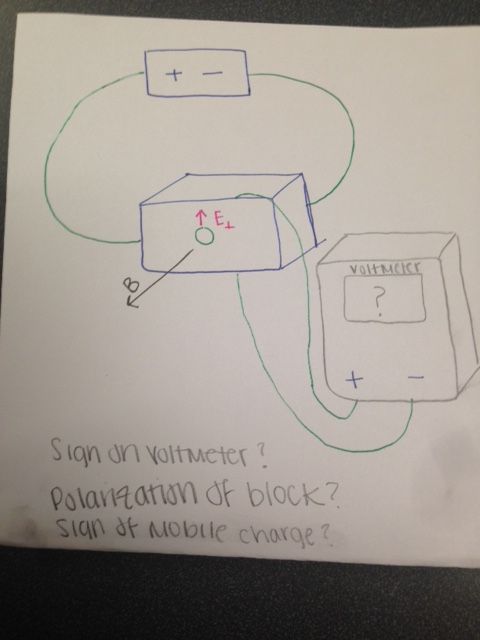
Question: A battery and metal block are connected by two wires. There is also a magnetic field coming out of the page. You are told that the Efield perpendicular is point in the positive y direction. There is also a voltmeter with the positive lead on the top of the block and the negative lead is on the bottom of the block. You are asked to find: the sign of the potential difference that the voltmeter will measure, the polarization of the block, and the sign of the mobile charge. (See attached diagram)

Examples with Calculation

These are the questions that involves numerical calculation with the application of Hall Effect. There are two problems, which aren't necessarily categorized in level of difficulty.

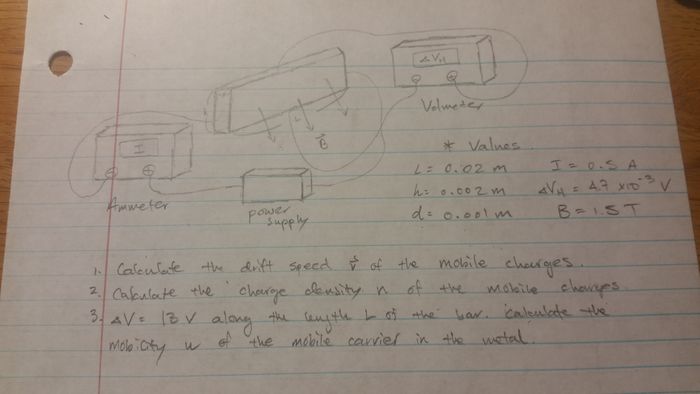
Problem #1

Click for Solution

Explanation: The voltmeter reads the voltage of the bar between the given distance. Since this voltmeter is attached along the height of the bar, the distance is going to be the 3cm. Anyways, we write out the Lorentz Force formula and equal it to zero, which makes the magnetic force and electric force equal to each other. After manipulating the equation, the Hall Electric Field is drift sped times the magnetic field. The drift speed is found by manipulating the Current formula, Area density formula, and the Resistance Formula. After I is found, you plug it into the I in the drift speed formula, and plug drift speed v into the Hall electric field formula. Since Hall voltage is Hall electric times the distance, you multiply the calculated Hall electric field with 3 cm in order to get the final Hall voltage.

Click for Solution

Explanation: You use the derivation of I from first portion of the question and plug in the values to calculate the conventional current. The Area here is the width times the height because the Ammeter is connected through the face created by the area of width and height.

Problem #2

Click for Solution

Explanation: First, you set up the Lorentz Force Equation equaling the net force of zero to the sum of magnetic force and electric force. After couple manipulation similar to first question, the Hall electric field equals to the product of the drift speed and magnetic field. Since, hall electric field is not given but hall voltage is, you have to substitute the hall electric field with hall voltage divided by the height of the bar (distance that voltmeter calculated). Afterwards, plug in all the given values, and calculate for the drift speed.

Click for Solution

Explanation: In order to find the charge density of the mobile charge carriers, you have to use the conventional current formula. You have to manipulate the conventional current formula to equal it to the charge density, and plug in all the values.

Click for Solution

Explanation: The drift speed of the particle is the product of the electric field and mobility of the particle. Since electric field is not given, but the voltage along the length of the bar is, you have to substitute the electric field with the given voltage divided by the length of the bar. Afterwards, plug in all the values given in the problem and calculate for the drift speed.

Important Tricks

Hall effect can only be tested so many ways. There are a few tricks to keep in mind.

for example look at the photo above. There a Voltmeter connected to a sheet of metal. SInce the voltmeter reads a negative voltage, you can automatically assume that the side connected to the negative terminal of the voltmeter is connected to the positive side of the metal due to hall effect. This is because that a voltmeter is reading a charge in the opposite direction.

You can try this in lab as well. Use a voltmeter and measure the voltage across a battery, if you switch between the positive and negative sides, then you also which between a positive and negative values. If the value is negative, then you are going in the opposite direction of the current.

CASE 2:

You have a conductive metal passing a wire with a voltage the blue X's are a magnetic field going into the page. Current of the Box is moving from the right to the left though the middle of the box, and as you can see from the voltameter, the siders are negative and positive polarized as listed in the picture. The negative voltage is due to the defection of electrons to the sensors in the voltameters.

Equilibrium is met in a problem with electric force is equal to a magnetic force, in this example, the electric field is from the polarized conductor.

So if Eh is the electric field from the hall effect, then the following is true of the system above in Equilibrium. Fe=Fb q*Eh=q*v*B so Eh=v*B

Where v is the velocity of the block entering the square wire Vh=(Voltage read on voltmeter)

Also note that if d is the width of the conductor, then the hall voltage Vh measured by the voltmeter is:

Vh=Eh*d=v*B*d

In this case, because F_b is (I*dl) X B, we can say that F_b points in the negative y direction. Since F_b must equal -F_e, F_e must point in the + y direction. E perpendicular does, so this means that our mobile charge is positive (See the previous problem for more explanation of finding the mobile charge). The polarization is determined by analyzing which way the magnetic force (before the Electric force cancels it out) pushes the mobile charge. In this case, the magnetic force pushes the positive mobile charge to the bottom, so negative mobile charges are at the bottom of the block to maintain neutrality. If the positive lead is connected to the place of higher potential (the positive polarization of the block), then the volt meter would read positive. In this case, the positive lead is connected to the place of lower potential, so the voltmeter would be negative.

Connectedness

How is this topic connected to something that you are interested in?

The Hall Effect can be as enjoyable as a puzzle. One has to pull the threads with all of the information that is given and connect the dots. Several key physics laws have to be applied, and the results can be quite practical. One practical application of the Hall Effect is the Hall Effect Sensor. It is a small sensor that will output a difference in voltage depending on the change in the magnetic field near the sensor. Thanks to this, one of the ways it is used is as a motion sensor, as described below.

How is it connected to your major?

Hall effect is all about seeing the relationship between magnetic and electric forces while also remembering how metals polarize. This means that it has a lot of mechanical and machine applications. It can sense when a magnetic field or electric field changes, so it can control many machines, apply pressures, and report many values. All of these skills are very important for Mechanical Engineering, so this topic has a lot of relevance to my major. Moreover, a lot of engineering, in general, is about analyzing concepts before calculating values. The idea of the Hall Effect gives a lot of important data without the use of any numbers (of course it gives more info on the calculation of numbers). This reasoning process required for the Hall Effect is a very helpful skill for engineers to have.

Hall Effect Sensor with an magnet

Hall Effect Sensor with an magnet

Hall Effect Sensor pinout

Another field that takes advantage of the Hall Effect is Electrical Engineering thanks to the Hall Effect Sensor. Electrical engineers can use the hall effect sensor to record movement. As seen in the pictures to the left and to the right, the sensor will increase its voltage the closer the magnet is to the sensor. In fact, a VIP group here at Georgia Tech, the VIP Hands-on Learning team, researched the possibility of using the sensor to measure the movement of a two-degree of freedom spring-mass system. Links to the VIP Research: https://vip.gatech.edu/wiki/index.php/Vibrations https://vip.gatech.edu/wiki/index.php/Hall_Effect_Sensor

Is there an interesting industrial application?

Hall Effects are used in industry to aid in the control of Hydraulic systems such as moving cranes and backhoes. It is also used to help sense a car wheel's motion to aid in the use of anti-skid/anti-lock brakes. Every smartphone today uses a hall effect sensor as well. This is how the digital compass of a cell phone works. The hall effect senses the change in magnetic field to approximate direction. Another great way of using the hall effect in smartphones is to lock the screen when a case cover is flipped. The cover has a magnet that the smartphone senses, so it locks the screen automatically when the cover is on the screen. A test for this feature can be seen in the following video: https://www.youtube.com/watch?v=ITbT5vrvhX8 .

Explore its application in a lab setting

Hall effect is also taken into consideration when hall probes are used as magnetometers.

A Hall probe is used to measure the difference of magnetic flux perpendicular to its sensor. this information is then fed to magnetometers to help read the difference in magnetic fields.

This is a link to buys a hall effect sensor. if you would ever want to buy one! http://www.ebay.com/sch/i.html?_nkw=hall+effect+sensor

and here is where you can buy a magnetometer http://www.ebay.com/itm/EM2-EARTH-MAGNETOMETER-MAP-MAGNETIC-FIELDS-SURVEY-TOOL-/251324557405?hash=item3a841c685d:m:m8gnViuidubx7vMbMejiNNA

To use this idea in a lab, simply create a circuit through a conductive material, like a piece of foil, and calculate the direction of the magnetic field using right-hand rule. Use this information to then properly add the hall probes to the foil so they are perpendicular to the magnetic field, and then BOOM! You will have information to read to a magnetometer.

History

Edwin Herbert Hall

The Hall Effect was discovered in 1879 by Edwin Hall while he was attending Johns Hopkins University for his Doctoral Degree. He exposed a gold leaf (metal slab) to a magnetic field perpendicular to its surface and had current flow through the slab. He observed a potential (delta V) perpendicular to the current and also the magnetic field. This means that potential is observed not only in the direction of current flow as usual. This is what led to Hall's discovery of the Hall Effect.

CONCLUSION: IF YOU WANT TO REMEMBER ANYTHING, THIS IS IT

1. When a current carrying metal/conductor is placed in a magnetic field, a voltage is formed perpendicular to both current and magnetic field

2. The Hall effect is made when the charges create almost a polarized metal, as a result the conductor experience charge carriers

3. Right-hand rule whenever in doubt.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Combining Electric and Magnetic Forces

Biot-Savart Law for Currents

Lorentz Force

Further reading

Books, Articles or other print media on this topic

Matter and Interactions: Volume 2 by Ruth Chabay and Bruce Sherwood (4th Edition)

http://www.phys.utk.edu/labs/modphys/Hall%20Effect.pdf

External links

Internet resources on this topic

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/hall.html

https://www.youtube.com/watch?v=_ATDraCQtpQ

References

https://en.wikipedia.org/wiki/Hall_effect

http://www.nobelprize.org/nobel_prizes/physics/laureates/1998/press.html

https://en.wikipedia.org/wiki/Edwin_Hall

Matter and Interactions: Volume 2 by Ruth Chabay and Bruce Sherwood (4th Edition)

http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/hall-edwin.pdf

http://www.electronics-tutorials.ws/electromagnetism/hall-effect.html

https://www.quora.com/What-is-the-use-of-Hall-effect-sensors-in-smartphones