Crystalline Structures: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
Bravais Lattices are the basic patterns that describe how points can be arranged in space to form a crystal lattice. Named after Auguste Bravais, who studied them in 1848, there are 14 unique Bravais lattices, each representing a distinct way to repeat a pattern in three dimensions. These lattices are grouped into seven crystal systems: cubic, tetragonal, orthorhombic, hexagonal, trigonal, monoclinic, and triclinic. Each lattice is defined by its symmetry and how it repeats in space, forming the backbone of all crystalline materials. Understanding Bravais lattices is important because they help explain how atoms are arranged in crystals and how this arrangement affects a material's properties like strength, conductivity, and optical behavior. | Bravais Lattices are the basic patterns that describe how points can be arranged in space to form a crystal lattice. Named after Auguste Bravais, who studied them in 1848, there are 14 unique Bravais lattices, each representing a distinct way to repeat a pattern in three dimensions. These lattices are grouped into seven crystal systems: cubic, tetragonal, orthorhombic, hexagonal, trigonal, monoclinic, and triclinic. Each lattice is defined by its symmetry and how it repeats in space, forming the backbone of all crystalline materials. Understanding Bravais lattices is important because they help explain how atoms are arranged in crystals and how this arrangement affects a material's properties like strength, conductivity, and optical behavior. | ||
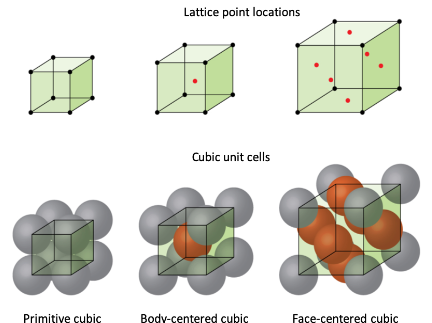
[[File:FCCBCC.png | [[File:FCCBCC.png]] | ||
===Body-Centered Cubic=== | ===Body-Centered Cubic=== | ||
Revision as of 22:27, 6 December 2024
Bravais lattices
Bravais Lattices are the basic patterns that describe how points can be arranged in space to form a crystal lattice. Named after Auguste Bravais, who studied them in 1848, there are 14 unique Bravais lattices, each representing a distinct way to repeat a pattern in three dimensions. These lattices are grouped into seven crystal systems: cubic, tetragonal, orthorhombic, hexagonal, trigonal, monoclinic, and triclinic. Each lattice is defined by its symmetry and how it repeats in space, forming the backbone of all crystalline materials. Understanding Bravais lattices is important because they help explain how atoms are arranged in crystals and how this arrangement affects a material's properties like strength, conductivity, and optical behavior.