Relative Velocity

This page defines and describes relative velocity.

The Main Idea

Velocity is a relative property, meaning that its value depends on the frame of reference from which it is observed and has no absolute "true" or "correct" value. This is because the position and therefore velocity of an object can only be defined relative to some coordinate system determined by the frame of reference chosen to model the situation. If two frames of reference are not moving with respect to each other, they will observe the same velocity for a given particle (even if their origins lie in different places), but if two frames of reference are moving with respect to each other, they will observe different velocity values for the same particle.

Consider a car driving down the highway. Suppose you want to determine the velocity of its driver. To do this, you must choose a frame of reference. You might choose the road, in which case the driver might have a velocity of 60mph in the northerly direction. However, you might also choose the car itself, in which case the driver would be at rest. The driver's position within the car does not change over time, so the velocity of the driver relative to the car is 0. You might even choose the center of the earth as a frame of reference, in which case the velocity of the driver would be more than 1000mph in the easterly direction due to the rotation of the earth (plus 60mph in the northerly direction because of the car's movement along the highway). The universe does not have a "natural" or "true" reference frame, so no choice of reference frame or observed velocity is more objectively correct than any other. That said, depending on why you want to know the driver's velocity, one choice of reference frame might be more useful to you than others for your specific situation. For example, if you are trying to determine how much danger the driver would be in in the event of a collision with a tree, you would want to know their velocity relative to that tree (which would be the same as their velocity relative to the road because the tree and the road are not moving with respect to each other). However, if you are trying to determine how much danger the driver would be in in the event of a collision with another car, you would want to know their velocity relative to that other car, which might be very low if the other car is traveling in the same direction or very high if the other car is traveling in the opposite direction.

A car moving left to one person can also be moving right to another person on the other side of the road. A frame of reference like this is known as an observational frame of reference. Differences in reference frames can result in problems varying slightly from person to person. On a coordinate axis, one reference frame may show direction to the left as moving along the negative x-axis while another may show that direction as moving along the positive x-axis.

Relative Velocity

When an object is moving in a medium that is also moving, its velocity may be different depending on the location of the observer. For example, consider a boat moving through a flowing river. If the observer is aboard the boat, the velocity will be different than if the observer was standing by the side of the river. This can be more easily described through vector addition with one reference frame considered an intermediate reference frame:

[math]\displaystyle{ \vec{v}_{AC} = \vec{v}_{AB} + \vec{v}_{BC} }[/math]

This means that the velocity of A with respect to C is equal to the sum of the velocity of A with respect to B and the velocity of B with respect to C. In this case, B is the intermediate reference frame.

Examples

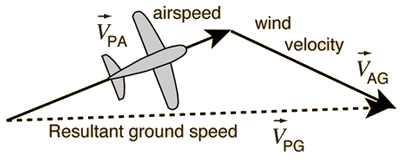
Airplane in Wind

An airplane is flying with a velocity of [math]\displaystyle{ \vec{v}_{PA} }[/math] relative to the air. The wind is moving with a velocity of [math]\displaystyle{ \vec{v}_{AG} }[/math] relative to an observer on the ground. The velocity of the plane relative to the ground can be found using vector addition:

[math]\displaystyle{ \vec{v}_{PG} = \vec{v}_{PA} + \vec{v}_{AG} }[/math]

Suppose the plane is moving with a velocity of [math]\displaystyle{ \left \langle {150,20,0} \right \rangle }[/math] km/h relative to the air. The wind is moving with a velocity of [math]\displaystyle{ \left \langle {-25,0,-10} \right \rangle }[/math] km/h relative to the ground. What is the velocity of the plane relative to the ground?

Answer:

[math]\displaystyle{ \vec{v}_{PG} = \left \langle {150,20,0} \right \rangle + \left \langle {-25,0,-10} \right \rangle }[/math]

[math]\displaystyle{ \vec{v}_{PG} = \left \langle {125,20,-10} \right \rangle }[/math]

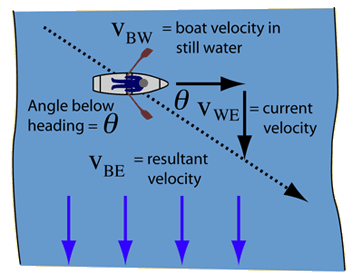
Boat in Current

A boat is moving straight across a river with a velocity of [math]\displaystyle{ \vec{v}_{BW} }[/math] relative to the water. The river has a current flowing perpendicular to the boat which has a velocity of [math]\displaystyle{ \vec{v}_{WE} }[/math] relative to the earth. The velocity of the boat relative to the Earth can be found using vector addition and the bearing of the boat can be found using trig relations:

[math]\displaystyle{ \vec{v}_{BE} = \vec{v}_{BW} + \vec{v}_{WE} }[/math]

[math]\displaystyle{ \Theta = \arctan \frac{\left \Vert \vec{v}_{WE} \right \|}{\left \Vert \vec{v}_{BW} \right \|} }[/math]

Suppose the boat is moving straight across the river with a velocity of 37 m/s relative to the water and the current is moving downstream and perpendicular to the boat with a velocity of 4 m/s relative to the earth. What is the velocity of the boat relative to the earth and what is its bearing?

Answer:

[math]\displaystyle{ \vec{v}_{BE} = \left \langle {37,0,0} \right \rangle + \left \langle {0,-4,0} \right \rangle }[/math]

[math]\displaystyle{ \vec{v}_{BE} = \left \langle {37,-4,0} \right \rangle }[/math]

[math]\displaystyle{ \Theta = \arctan \frac{4}{37} }[/math]

[math]\displaystyle{ \Theta = 6.17018^\circ }[/math]

See also

• Velocity
• Speed vs Velocity
• Derivation of Average Velocity
• 2-Dimensional Motion

External links

HyperPhysics: Relative Motion

References

HyperPhysics: Relative Motion

Example from Frame of Reference