Magnetic Field of a Disk

Main Idea

Through this page, you will understand how to solve for the magnetic field produced by a rotating, charged, circular disk.

First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object allowed them to produce unique electric fields.

In order to figure out this magnetic field, we will start from the fundamental principles that we have learned already with regards to how magnetic fields are produced. We will then build on that and include the geometry of the object in question, in this a circular disk, in order to solve for the magnetic field produced by this disk.

Mathematical Model

Say we have a "flat" circular disk with radius [math]\displaystyle{ R }[/math] and carrying a uniform surface charge density [math]\displaystyle{ \sigma }[/math]. It rotates with an angular velocity [math]\displaystyle{ \omega }[/math] about the z-axis.

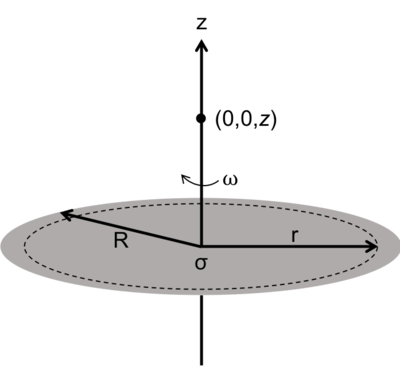
To find the magnetic field [math]\displaystyle{ B }[/math] at any point [math]\displaystyle{ z }[/math] along the rotation axis, we can consider the disk to be a collection of concentric current loops. Breaking the disk into a series of loops with infinitesimal width [math]\displaystyle{ dr }[/math] and with radius [math]\displaystyle{ r }[/math], we will have an infinitesimal area for loop :

[math]\displaystyle{ dA = 2\pi r dr }[/math], where

[math]\displaystyle{ A = \pi r^2 }[/math]

And therefore have an infinitesimal charge on each loop of:

[math]\displaystyle{ dQ = 2\pi \sigma rdr }[/math], where

[math]\displaystyle{ Q = \sigma A }[/math]

This loop is rotating at an angular velocity [math]\displaystyle{ \omega }[/math], which means the charge [math]\displaystyle{ dQ }[/math] on our loop makes a full rotation around the axis every period,

[math]\displaystyle{ T = \frac{2\pi}{\omega} }[/math] seconds.

Since a charge [math]\displaystyle{ dQ }[/math] makes a full rotation every [math]\displaystyle{ T }[/math] seconds, our infinitesimally thin ring is a current loop with an infinitesimal current:

[math]\displaystyle{ dI = \frac{dQ}{T} = \frac{2\pi \sigma rdr}{\frac{2\pi}{\omega}} = \sigma \omega rdr }[/math], where

[math]\displaystyle{ I = \frac{Q}{t} }[/math]

For this single loop, equivalent to a current [math]\displaystyle{ dI }[/math], we can calculate the field a distance [math]\displaystyle{ z }[/math] above the axis. Using this proof from the Magnetic Field of a Loop page, we can get:

[math]\displaystyle{ dB = \frac{\mu_0 r^2 dI}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} }[/math]

Now to find the total magnetic field for all of the concentric rings, we must integrate from [math]\displaystyle{ r = 0 }[/math] to [math]\displaystyle{ r = R }[/math]:

[math]\displaystyle{ B = \int_{0}^{R} \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}} }[/math]

[math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{0}^{R} }[/math]

[math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+R^2}{\sqrt{R^2+z^2}} - 2|z| \right] }[/math]

The absolute value around the [math]\displaystyle{ z }[/math] is important because we want the field to be the same on either side of the disk, whether we are in the positive z or negative z direction.

Computational Model

Insert Computational Model here

Examples

Simple

An infinitely thin disk with radius [math]\displaystyle{ R = 2 \text{m} }[/math] is spinning at a rate of [math]\displaystyle{ \omega = 15\pi \ \frac{rads}{s} }[/math]. The disk has a uniform charge density [math]\displaystyle{ \rho = 2 \ \frac{C}{A} }[/math]. Imagine the disk is lying flat in the xy-plane.

a) What is the magnetic field [math]\displaystyle{ 5 \text{ m} }[/math] above the axis of rotation. What about [math]\displaystyle{ 5 \text{ m} }[/math] below the axis of rotation?

Middling

A uniformly charged disk of radius [math]\displaystyle{ R = 0.01 \ \text{m} }[/math] is is rotating at a rate of [math]\displaystyle{ \omega = 2\pi \ \frac{\text{rads}}{s} }[/math] and is losing charge to its surroundings in such a way that the charge density of the disk is changing by [math]\displaystyle{ \sigma (t) = \sigma_0 te^{-\frac{5t^2}{\pi}} }[/math], where [math]\displaystyle{ t }[/math] is time in seconds, [math]\displaystyle{ \sigma_0 = 3 \ \frac{C}{A \cdot s} }[/math].

a) What is the magnetic field at time [math]\displaystyle{ t_0 = 0 }[/math]

See also

Further reading

• Matter and Interactions Vol. II
• Magnetic Fields of Spinning Disk and Sphere

External links

• Magnetic Field of a Long Straight Wire
  
• Magnetic Field of a Loop
  
• Biot-Savart Law
  
• Biot-Savart Law for Currents
  
• Current