Magnetic Field of a Disk

Main Idea

Through this page, you will understand how to solve for the magnetic field produced by a rotating, charged, circular disk.

First, let us start with the basics. We know that moving charges spread out over the surface of an object will produce a magnetic field. This is similar to the concept of how charges spread out over an object allowed them to produce unique electric fields.

In order to figure out this magnetic field, we will start from the fundamental principles that we have learned already with regards to how magnetic fields are produced. We will then build on that and include the geometry of the object in question, in this a circular disk, in order to solve for the magnetic field produced by this disk.

Mathematical Model

Say we have a "flat" circular disk with radius [math]\displaystyle{ R }[/math] and carrying a uniform surface charge density [math]\displaystyle{ \sigma }[/math]. It rotates with an angular velocity [math]\displaystyle{ \omega }[/math] about the z-axis.

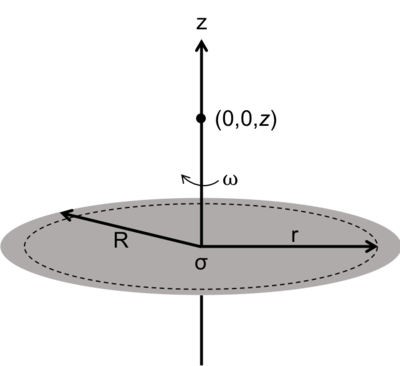
To find the magnetic field [math]\displaystyle{ B }[/math] at any point [math]\displaystyle{ z }[/math] along the rotation axis, we can consider the disk to be a collection of concentric current loops. Breaking the disk into a series of loops with infinitesimal width [math]\displaystyle{ dr }[/math] and with radius [math]\displaystyle{ r }[/math], we will have an infinitesimal area for loop :

[math]\displaystyle{ dA = 2\pi r dr }[/math], where

[math]\displaystyle{ A = \pi r^2 }[/math]

And therefore have an infinitesimal charge on each loop of:

[math]\displaystyle{ dQ = 2\pi \sigma rdr }[/math], where

[math]\displaystyle{ Q = \sigma A }[/math]

This loop is rotating at an angular velocity [math]\displaystyle{ \omega }[/math], which means the charge [math]\displaystyle{ dQ }[/math] on our loop makes a full rotation around the axis every period,

[math]\displaystyle{ T = \frac{2\pi}{\omega} }[/math] seconds.

Since a charge [math]\displaystyle{ dQ }[/math] makes a full rotation every [math]\displaystyle{ T }[/math] seconds, our infinitesimally thin ring is a current loop with an infinitesimal current:

[math]\displaystyle{ dI = \frac{dQ}{T} = \frac{2\pi \sigma rdr}{\frac{2\pi}{\omega}} = \sigma \omega rdr }[/math], where

[math]\displaystyle{ I = \frac{Q}{t} }[/math]

For this single loop, equivalent to a current [math]\displaystyle{ dI }[/math], we can calculate the field a distance [math]\displaystyle{ z }[/math] above the axis. Using this proof from the Magnetic Field of a Loop page, we can get:

[math]\displaystyle{ dB = \frac{\mu_0 r^2 dI}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} }[/math]

Now to find the total magnetic field for all of the concentric rings, we must integrate from [math]\displaystyle{ r = 0 }[/math] to [math]\displaystyle{ r = R }[/math]:

[math]\displaystyle{ B = \int_{0}^{R} \frac{\mu_0 r^3 \sigma \omega dr}{2(r^2+z^2)^{3/2}} = \frac{\mu_0 \sigma\omega}{2} \int_{0}^{R} \frac{r^3 dr}{(r^2+z^2)^{3/2}} }[/math]

[math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+r^2}{\sqrt{r^2+z^2}}\right]_{0}^{R} }[/math]

[math]\displaystyle{ B = \frac{\mu_0 \sigma\omega}{2} \left[\frac{2z^2+R^2}{\sqrt{R^2+z^2}} - 2|z| \right] }[/math]

The absolute value around the [math]\displaystyle{ z }[/math] is important because we want the field to be the same on either side of the disk, whether we are in the positive z or negative z direction.

Computational Model

Insert Computational Model here

Examples

Simple

An infinitely thin disk with radius [math]\displaystyle{ R = 2 \text{ m} }[/math] is spinning counter-clockwise at a rate of [math]\displaystyle{ \omega = 15\pi \ \frac{rads}{s} }[/math]. The disk has a uniform charge density [math]\displaystyle{ \rho = 2 \ \frac{C}{A} }[/math]. Imagine the disk is lying flat in the xy-plane.

a) What is the magnitude and direction of the magnetic field [math]\displaystyle{ 5 \text{ m} }[/math] above the axis of rotation. What about [math]\displaystyle{ 5 \text{ m} }[/math] below the axis of rotation?

Using a convenient right-hand rule, we curl our fingers in the direction of rotation (AKA the direction of the current). the way our thumb points is the direction of the magnetic field: the (+z) direction.

To find the magnitude of the magnetic field [math]\displaystyle{ 5 }[/math] meters above the disk, we will call upon our Mathematical Model:

[math]\displaystyle{ B = \frac{\mu_0 \sigma \omega}{2}\left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math], where in our case

[math]\displaystyle{ \begin{align} \sigma & = \rho = 2 \\ \omega & = 15\pi \\ R & = 2 \\ z & = 5 \\ \end{align} }[/math]

We will plug these values in to get:

[math]\displaystyle{ \begin{align} B & = \frac{\mu_0 \times 2 \times 15\pi}{2}\left[\frac{2(5)^2 + (2)^2}{\sqrt{(5)^2 + (2)^2}} - 2|5| \right] \\ & = \mu_0 \times 15\pi \left[\frac{50 + 4}{\sqrt{25 + 4}} - 10 \right] \\ & = \mu_0 \times 15\pi \left[\frac{54}{\sqrt{29}} - 10 \right] \\ B & = 1.63 \times 10^{-6} \text{ T} \end{align} }[/math]

Therefore, the rotating, charged disk is creating a magnetic field above the disk pointing "up" with a magnitude of [math]\displaystyle{ 1.63 \times 10^{-6} \text{ T} }[/math].

To find the direction of the magnetic field below the disk, we once again employ the right-hand rule: our fingers curl in the direction of rotation and we find the magnetic field points in the (+z) direction again.

To find the magnitude of the magnetic field [math]\displaystyle{ 5 }[/math] meters below the disk, we will use the same formula from above:

[math]\displaystyle{ B = \frac{\mu_0 \sigma \omega}{2}\left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math], where in our case:

[math]\displaystyle{ \begin{align} \sigma & = \rho = 2 \\ \omega & = 15\pi \\ R & = 2 \\ z & = -5 \\ \end{align} }[/math]

We will plug these values in to get:

[math]\displaystyle{ \begin{align} B & = \frac{\mu_0 \times 2 \times 15\pi}{2}\left[\frac{2(-5)^2 + (2)^2}{\sqrt{(-5)^2 + (2)^2}} - 2|-5| \right] \\ & = \mu_0 \times 15\pi \left[\frac{50 + 4}{\sqrt{25 + 4}} - 10 \right] \\ & = \mu_0 \times 15\pi \left[\frac{54}{\sqrt{29}} - 10 \right] \\ B & = 1.63 \times 10^{-6} \text{ T} \end{align} }[/math]

Therefore, the rotating, charged disk is creating a magnetic field below the disk pointing "up" with a magnitude of [math]\displaystyle{ 1.63 \times 10^{-6} \text{ T} }[/math].

Notice the the magnitude and direction of the magnetic field at the two points are equal. This is no coincidence. In general, if [math]\displaystyle{ z_1 = a }[/math] and [math]\displaystyle{ z_2 = -a }[/math], then they will have the same direction and magnitude for the magnetic field (for a rotating disk).

Middling

A uniformly charged disk of radius [math]\displaystyle{ R = 0.01 \ \text{m} }[/math] is rotating at a rate of [math]\displaystyle{ \omega = 2\pi \ \frac{\text{rads}}{s} }[/math] and is losing its charge to its surroundings in such a way that the charge density of the disk is decreasing by [math]\displaystyle{ \frac{d \sigma}{dt} = \pi te^{-\frac{5t^2}{\pi}} }[/math], where [math]\displaystyle{ t }[/math] is time in seconds.

a) What is the magnitude of the magnetic field at time [math]\displaystyle{ t_0 = 0 }[/math] along the axis of rotation, if the charge density is [math]\displaystyle{ 3 \ \frac{C}{A} }[/math] at this time?

We can immediately use our Mathematical Model to solve for the magnetic field:

[math]\displaystyle{ B(z) = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] }[/math], where

[math]\displaystyle{ z }[/math] is a point along the axis of rotation

In our case the following values have been specified for us:

[math]\displaystyle{ \begin{align} \sigma & = 3 \\ \omega & = 2\pi \\ R & = 0.01 \\ \end{align} }[/math]

Therefore, we can plug these values in and simplify for an answer:

[math]\displaystyle{ \begin{align} B(z) & = \frac{\mu_0 \sigma \omega}{2} \left[\frac{2z^2 + R^2}{\sqrt{z^2 + R^2}} - 2|z| \right] \\ & = \frac{\mu_0 \times 3 \times 2\pi}{2} \left[\frac{2z^2 + (0.01)^2}{\sqrt{z^2 + (0.01)^2}} - 2|z| \right] \\ B(z) & = \left(1.184 \times 10^{-5}\right) \left[\frac{2z^2 + \left(1 \times 10^{-4}\right)}{\sqrt{z^2 + \left(1 \times 10^{-4}\right)}} - 2|z| \right]\\ \end{align} }[/math]

b) What is the magnetic field at time [math]\displaystyle{ t_f = 10 \ s }[/math] ?

(1) Integrate/Solve [math]\displaystyle{ \frac{d \sigma}{dt} }[/math] for [math]\displaystyle{ \sigma (t) }[/math]

To find the magnitude of the magnetic field, we will have to find the new charge density, since we were told it is decreasing with time. To do this, we will integrate [math]\displaystyle{ \frac{d \sigma}{dt} }[/math] to solve for [math]\displaystyle{ \sigma (t) }[/math]:

[math]\displaystyle{ \frac{d \sigma}{dt} = \pi te^{-\frac{5t^2}{\pi}} }[/math]

or:

[math]\displaystyle{ d \sigma = \left[ \pi te^{-\frac{5t^2}{\pi}} \right] dt }[/math]

or:

[math]\displaystyle{ \int d \sigma = \int \pi te^{-\frac{5t^2}{\pi}} \ dt }[/math]

or:

[math]\displaystyle{ \begin{align} \sigma (t) & = \int \pi te^{-\frac{5t^2}{\pi}} \ dt \\ & = \pi \int te^{-\frac{5t^2}{\pi}} \ dt \\ & = \pi \int -\frac{\pi}{10} e^u du \ \text{ where } u = -\frac{5t^2}{\pi} \text{ and } du = -\frac{10}{\pi} t \ dt \\ & = -\frac{\pi^2}{10} \int e^u du \\ & = -\frac{\pi^2}{10} \left[e^u \right] + C\\ \sigma (t) & = -\frac{\pi^2}{10} \left[e^{-\frac{5t^2}{\pi}} \right] + C \\ \end{align} }[/math]

To find [math]\displaystyle{ C }[/math] we use the original charge density of time [math]\displaystyle{ t_0 = 0 }[/math]:

[math]\displaystyle{ \sigma (0) = 3 }[/math]

Therefore:

[math]\displaystyle{ 3 = -\frac{\pi^2}{10} \left[e^{-\frac{5(0)^2}{\pi}} \right] + C }[/math]

[math]\displaystyle{ C = 3 + \frac{\pi^2}{10} }[/math]

This gives [math]\displaystyle{ \sigma (t) }[/math] as:

[math]\displaystyle{ \begin{align} \sigma (t) & = \\ & = \\ & = \\ & = \\ & = \\ \end{align} }[/math]

Now we can find [math]\displaystyle{ \sigma (10) }[/math]:

[math]\displaystyle{ \sigma (10) = -\frac{\pi^2}{10} \left[e^{-\frac{5(10)^2}{\pi}} + \right] }[/math]

(2) Find [math]\displaystyle{ C }[/math]

(3) FInd [math]\displaystyle{ \sigma (10) }[/math]

(4) Plug into magnetic field equation

Difficult

Two concentric infinitely thin disks are rotating in opposite directions in the xy-plane. Disk 1 [math]\displaystyle{ (D_1) }[/math] is the inner disk, with a radius of [math]\displaystyle{ R_1 = 1 \text{ m} }[/math]; it is rotating counter-clockwise at a rate of [math]\displaystyle{ \omega_1 = 10 \ \frac{\text{rads}}{s} }[/math]. Disk 2 [math]\displaystyle{ (D_2) }[/math] is the outer disk, with a radius of [math]\displaystyle{ R_2 = 5 \text{ m} }[/math]; it is rotating clockwise at a rate of [math]\displaystyle{ \omega_2 = 3 \ \frac{\text{rads}}{s} }[/math]. See [1] for clarification.

a) What is the direction of the magnetic field created by [math]\displaystyle{ D_1 }[/math] at a point along the axis of rotation and above the disk? What is the direction of the magnetic field created by [math]\displaystyle{ D_2 }[/math] at a point along the axis of rotation and above the disk?

b) What is the magnitude of the net magnetic field [math]\displaystyle{ 0.13 \text{ m} }[/math] along the axis of rotation and above the disks?

See also

Further reading

• Matter & Interactions Vol. II
• Magnetic Fields of Spinning Disk and Sphere

External links

• Magnetic Field of a Long Straight Wire
  
• Magnetic Field of a Loop
  
• Biot-Savart Law
  
• Biot-Savart Law for Currents
  
• Current
  

References

• Matter & Interactions Vol. II