Detecting a Magnetic Field

The Main Idea

A compass can be used to determine the magnetic field in a wire. If a compass is not in the proximity of any iron or steel object, the compass will naturally point in the direction of the Earth's magnetic north pole. If a current carrying wire is brought near the compass, the compass needle will deflect in the direction of the net magnetic field.

This shows the Magnetic Field around a wire. The field above and below are in opposite directions which Oerested determined.

A Mathematical Model

A useful attribute of a compass is that you can calculate the the magnetic field of current carrying wire when you figure out the deflection angle. This equation is: [math]\displaystyle{ B_{wire}=B_{earth} tan(\theta) }[/math] where [math]\displaystyle{ \theta }[/math] is the deflection angle, [math]\displaystyle{ B_{earth} }[/math] is the earth's magnetic field which is a constant value of 2e-5 Tesla.

A Computational Model

Take a minute to watch this video that shows Oersted's Experiment. It is very similar to what we did in lab. Video Showing Oersted Effect

Examples

Simple

Problem 17.2.XP.003 from Matter and Interactions Book:

A current-carrying wire oriented north-south and laid over a compass deflects the compass 18° to the east. What is the magnitude of the magnetic field made by the current? The horizontal component of Earth's magnetic field is about [math]\displaystyle{ 2 ✕ 10^{-5} tesla }[/math] .

[math]\displaystyle{ B_{wire}=B_{earth} tan(\theta) }[/math]

[math]\displaystyle{ B_{wire}= 2 ✕ 10^{-5} tesla ✕ tan(18) }[/math]

[math]\displaystyle{ B_{wire}= 6.49✕ 10^{-6} }[/math]Tesla

What direction does the electron current flow in the wire?

The electron current flows from south to north.

Middling

Problem 17.7.035 from Matter and Interactions Book:

Deflecting a compass needle

When you bring a current-carrying wire down onto the top of a compass, aligned with the original direction of the needle and 4 mm above the needle, the needle deflects by θ = 12 degrees (see the figure).

*The magnetic field under the wire, due to the current, points East. *Electron current in the wire is flowing upward(North). *Conventional Current in the wire is flowing downward(South).

Calculate the amount of conventional current flowing in the wire. The measurement was made at a location where the horizontal component of the Earth's magnetic field is [math]\displaystyle{ B_{Earth}= 2 ✕ 10^{-5} }[/math] tesla.

[math]\displaystyle{ B_{wire}=B_{earth} ✕ tan(\theta) }[/math]

[math]\displaystyle{ B_{wire}= 2 ✕ 10^{-5} tesla ✕ tan(12) }[/math]

[math]\displaystyle{ B_{wire}= 4.25✕ 10^{-6} }[/math]Tesla

Given: [math]\displaystyle{ B_{wire}= 4.25✕ 10^{-6} }[/math]Tesla, r=.004 m,[math]\displaystyle{ {\mu_{0}\over4\pi}=1e-7 }[/math]; Solve for I:

[math]\displaystyle{ B_{wire}={\mu_{0}\over4\pi}{2I\over r} }[/math]

[math]\displaystyle{ 4.25✕ 10^{-6}=1e-7{2I\over .004} }[/math]

[math]\displaystyle{ I={{.004✕4.25✕ 10^{-6}}\over {2✕ {1✕ 10^{-7}}}} }[/math]

I=.085 Amperes

Difficult

Problem 17.7.038 from Matter and Interactions Book:

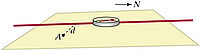
A long current-carrying wire, oriented North-South, lies on a table (it is connected to batteries which are not shown). A compass lies on top of the wire, with the compass needle about 3 mm above the wire. With the current running, the compass deflects 16 degrees to the West. At this location, the horizontal component of the Earth's magnetic field is about 2e-5 tesla.

What is the magnitude of the magnetic field at location A, on the table top, a distance 2.5 cm to the East of the wire, due only to the current in the wire?

Solving:

[math]\displaystyle{ B_{wire}=B_{earth}tan(\theta) }[/math]

[math]\displaystyle{ B_{wire}=2e-5*tan(16) }[/math]

[math]\displaystyle{ B_{wire}=5.735e-6 T }[/math]

[math]\displaystyle{ B_{wire}={\mu_{0}\over4\pi}{2I\over r} }[/math] Where r is the distance the wire is from the compass.

Given: [math]\displaystyle{ B_{wire}=5.735e-6 }[/math] T, r= 0.003 m, and [math]\displaystyle{ {\mu_{0}\over4\pi}=1e-7; }[/math] Solve for the current :I

[math]\displaystyle{ {5.735e-6}={1e-7}{2I\over .003} }[/math]

[math]\displaystyle{ {{{5.735e-6}*{.003}}\over{1e-7 *2}}={I} }[/math]

I=.086 A

[math]\displaystyle{ B_{wire}={\mu_{0}\over4\pi}{2I\over d} }[/math] Now solve for the new [math]\displaystyle{ B_{wire} }[/math] given the current: I=.086 A and the new location d= .025m

[math]\displaystyle{ B_{wire}={1e-7} {{2*.086}\over .025} }[/math]

[math]\displaystyle{ B_{wire}= }[/math]6.882 e-7 T

Connectedness

There are many applications of the idea behind this topic. There are many electromagnetic devices where you are able to manipulate the magnetic field by varying the current running through the device. A good example is a speaker. There are electromagnets inside of the speaker and when you vary the current running through the wires around them you vary the output of the speaker.

Any engineering major knows that there is a great amount of physics behind what you do. Physics and engineering are heavily intertwined.

History

Hans Oersted

This phenomenon was discovered by Danish scientist, Hans Oersted in 1826. After stumbling upon the deflection of a needle, he further investigated the math behind the event. He discovered that the magnitude of the magnetic field depends on the amount of current; if there is no current there will be no magnetic field. He also discovered that the deflection direction of the compass when the wire is above the wire is opposite the deflection direction when the wire is below the wire. This was the start of understanding magnetic fields.

See also

There are many other wiki pages relating to magnetic fields in this physics wiki. One I would recommend is

Biot-Savart Law for Currents

This page gives the equation used to find the magnetic field when given a current which is what we used in this page. The math can explain the concept of the current changing the magnitude of the magnetic field. This magnetic field causes the deflection of the compass.

Further reading

Exploring Magnetic Fields With a Compass Article describing what happens when a compass is brought near a current carrying wire.

External links

Magnetic Fields

References

Chabay, R. & Sherwood, B. (2015). Matter and Interactions(4th Ed)(Vol 2). North Carolina: John Wiley & Sons,Inc.

Hans Christian Oersted. Digital image. MagCraft. National Imports, 2015. Web. 18 Nov. 2015. <http://www.rare-earth-magnets.com/hans-christian-oersted/>

Kurtus, Ron. "Electromagnetic Devices." By Ron Kurtus. School for Champions. Web. 29 Nov. 2015. <http://www.school-for-champions.com/science/electromagnetic_devices.htm#.Vlsxtd-rTVo>..

32 Oersted's Effect.mpg. Perf. Science Demo LTD. Youtube. N.p., 24 Oct. 2010. Web. 29 Nov. 2015. <https://www.youtube.com/watch?v=lwjk789NaVQ>.

Lunk, Brandon, and Robert Beichner. "Exploring Magnetic Fields With a Compass." The Physics Teacher 49 (2011): 45-48. 2011. Web. 29 Nov. 2015. <https://www.physics.ncsu.edu/physics_ed/Articles/LunkBFieldArticle.pdf>.

Page initiated by --Ejohnston8 (talk)