Poynting Vector

Claimed by Tanner Shaw (tshaw30)

The Poynting vector represents the direction and magnitude of the flux in energy from an electromagnetic field. It was originally discovered by John Henry Poynting in 1884.

The Main Idea

The poynting vector describes the magnitude and direction of the flux in energy from an electromagnetic field.

A Mathematical Model

A graphical representation of the poynting vector

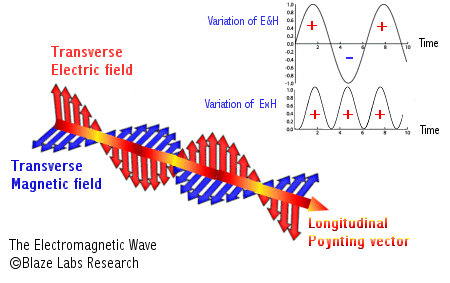
The poynting vector can be derived by the equation [math]\displaystyle{ \vec{S} = {\frac{1}{μ_0}}\vec{E}\times\vec{B} }[/math] where E is the electric field vector, and B is the magnetic field vector, and μ₀ is the magnetic constant. A cross product is needed to compute the poynting vector, so being familiar with the right-hand-rule can help to conceptualize and/or check your answer for problems asking to find it.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Easy Problem

An electron is travelling in the -X direction in the XY plane. At a certain instant, you observe the electron from a location as seen in the diagram. What is the direction of the poynting vector from your location?

The

Moderate

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Intermediate Problem

A proton is moving in the +X direction at two thirds the speed of light in the XY plane. At a certain instance, your observation location is 3e-8 m in the -Y direction from the proton. Calculate the poynting vector at this observation location from the moving proton.

In order to solve this problem, we must calculate both the electric and magnetic fields caused by the moving particle at the observation location. To solve for the electric field we will use the formula for calculating electric fields from point charges, [math]\displaystyle{ \vec{E} = {\frac{1}{4πε_0}}{\frac{Q}{r^2}}\hat{r} }[/math].

Therefore, we must solve:

[math]\displaystyle{ \vec{E} = (9\times10^9\frac{N\times m^2}{C^2}){\frac{(1.6\times10^{-19} C)}{({3\times10^{-8} m})^2}} \lt 0,-1,0\gt }[/math]

Which will give us:

[math]\displaystyle{ \vec{E} = \lt 0, 1.6\times10^6,0\gt \frac{N}{C} }[/math]

Now that we have the electric field at the observation location, all we have left to calculate is the magnetic field. The equation of the magnetic field due to a moving point charge is [math]\displaystyle{ \vec{B} = {\frac{μ_0}{4π}} Q{\frac{\vec{v}\times\hat{r}}{r^2}} }[/math]

Therefore, we must solve:

[math]\displaystyle{ \vec{B} = (1\times10^{-7}{\frac{T\times m}{A}})(1.6\times10^{-19}C){\frac{\lt 2\times10^8,0,0\gt {\frac{m}{s}} \times\lt 0,-1,0\gt }{(3\times10^{-8}m)^2}} }[/math]

Which gives us:

[math]\displaystyle{ \vec{B} = \lt 0,0,-3.56\times10^{-3}\gt T }[/math]

Using the equation [math]\displaystyle{ \vec{S} = {\frac{1}{μ_0}}\vec{E}\times\vec{B} }[/math], we can find the answer.

[math]\displaystyle{ \vec{S} = (\frac{1}{4π\times10^{-7}})\lt 0, 1.6\times10^6,0\gt \frac{N}{C}\times\lt 0,0,-3.56\times10^{-3}\gt T }[/math]

[math]\displaystyle{ \vec{S} = \lt -4.53\times10^9, 0, 0\gt \frac{W}{m^2} }[/math]

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

John Henry Poynting, an English physicist and professor, was the first to derive the equation that described the direction of electromagnetic flux. His work for the equation was published in 1884. Nikolay Umov and Oliver Heaviside both independently discovered the poynting vector as well.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page