Energy and Momentum Analysis in Radiation

Claimed by Sneh Munshi

The Main Idea

Electromagnetic Radiations in the Classical Model

Electromagnetic radiation can essentially be described as stream of photons. These photons are defined as chargeless and massless, however they have both energy and surprisingly, given their lack of mass, momentum, which can be calculated from their wave properties.

Waves were poorly understood until the 1900s, when Max Planck and Albert Einstein developed modern corrections to classical theory.

Planck theorized that "black bodies" or thermal radiators and other forms of electromagnetic radiation existed not as a continuous spectrum but rather in discrete or "quantized" form. This implied that there were only certain energy values that an electromagnetic wave could have.

In the classical model that we study now it is mentioned that electromagnetic radiation carries both momentum and energy, and can impart both energy and momentum to matter. We shall discuss these ideas in more detail.

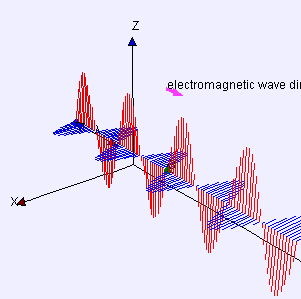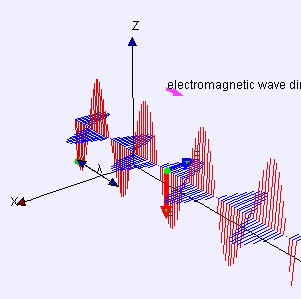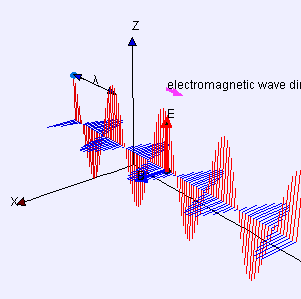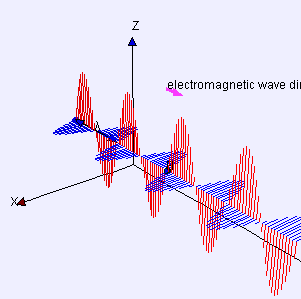
Mathematical Model and Related Concepts

Energy in Electromagnetic Radiation

Let's start by understanding how a pulse of electromagnetic radiation would interact with ordinary matter. To see this effect, we shall look at a single charged particle interacting with the electromagnetic radiation which is composed of perpendicular electric and magnetic fields and see what happens when the pulse of radiation goes by.

Until the pulse reaches the charged particle nothing happens. Now let's assume that the electromagnetic radiation has a width of "w" so the pulse would last for a short time (w/c) where c is the speed of light. Now upon the arrival of the pulse, the charged particle (assuming it is positive) experiences a force (F = qE, where E is the magnitude of the electric field in the electromagnetic radiation) in the direction of the electric field that comprises the radiation and this brief impulse i.e. the product of force and time duration gives the charged particle a momentum. According to the Newton's Second Law of Motion:

[math]\displaystyle{ \Delta p = p - 0 = F \Delta t = (qE)*(w/c) }[/math]

Now this interaction is over so quickly that the charged particle hardly has the time to move a significant distance in the direction of the field. However, if attach the charged particle to a spring then it will oscillate to and fro in the direction of applied force. Since the kinetic energy of the charged particle has to come from somewhere, we conclude that it was imparted to the charged particle by the radiation which means that the there must be some energy carried by the electromagnetic radiation which was transferred.

Since the momentum is proportional to the magnitude of the electric field E in the pulse, we have the following:

[math]\displaystyle{ \Delta K = K - 0 \approx \frac{p^2}{2m} = (qE \frac{w}{c})^2(\frac{1}{2m}) }[/math]

Now if we assume that the speed of this charged particle is very small compared to the speed of light then we can see that the radiative energy is directly proportional to the square of the electric field of the radiation. Also by the conservation of energy principle we know that the since the charged particle has gained energy, the radiation should have lost an equal amount of energy and therefore, the electric field E should be smaller after the pulse has accelerated the charged particle.

Energy Density

ENERGY DENSITY IN ELECTRIC AND MAGNETIC FIELDS

[math]\displaystyle{ \frac{Energy}{Volume} = \frac{1}{2} \epsilon_0 E^2 + \frac{1}{2} \frac{1}{\mu_0} B^2 }[/math]

ENERGY DENSITY IN ELECTROMAGNETIC RADIATION

[math]\displaystyle{ \frac{Energy}{Volume} = \frac{1}{2} \epsilon_0 E^2 + \frac{1}{2} \frac{1}{\mu_0} (\frac{E}{c})^2 = \frac{1}{2} \epsilon_0 E^2(1 + \frac{1}{\mu_0 \epsilon_0 c^2}) = \epsilon_0 E^2 }[/math]

Energy Density is related to energy "flux" in joules per second per square meter. We define a "Poynting vector" [math]\displaystyle{ \overrightarrow{S} }[/math], whose magnitude is the rate of energy flux (in watts per square meter) and whose direction is the direction of propagation of the electromagnetic radiation:

ENERGY FLUX

[math]\displaystyle{ \overrightarrow S = \frac{1}{\mu_0} \overrightarrow E \times \overrightarrow B }[/math]

Momentum in Electromagnetic Radiation

We just studied the effect of the electric field in a pulse of radiation which causes a charged object to move in a direction perpendicular to the direction of propagation of the radiation. However, the magnetic field of the radiation also has an interesting effect although it is very small and therefore, hard to observe but we shall discuss that now.

Let's consider the charged particle again. Now when the electric field has imparted some momentum [math]\displaystyle{ \Delta p }[/math] to it, the magnetic field will also exert a force on the moving charge and let's say it has a speed v. On applying the right hand rule and considering both the positively charged particle and negatively charged particle, we realize that the magnetic force is in the same direction regardless of the sign of the charge and this effect that the electromagnetic radiation has on matter is called "radiation pressure". Note that this pressure even acts on neutral matter and that is because it has the same effect on protons and electrons of the neutral matter but this effect is hard to observe since it is a small effect.

The ratio of the average magnetic force to the electric force is as follows:

[math]\displaystyle{ \frac{\overline F_m}{\overline F_e} = \frac{q (v/2) (E/c)}{q E} = \frac{1}{2} \frac{v}{c} }[/math]

Usually, the speed v acquired during the passage of the pulse is very small as compared to the speed of light so the effect of the magnetic field of the radiation is very small as compared to the effect of the electric field.

Momentum Carried by Electromagnetic Radiation

When a charged particle is exposed to a sinusoidal electromagnetic radiation, in the direction of the electric field which is perpendicular to the direction of propagation of the pulse, there is no net gain in momentum and this is because of the alternating electric field whose net electric force on the particle cancels out to be zero.

However, the average magnetic force on the particle would not be zero, as the magnetic force acts in the direction of propagation of the radiation i.e. [math]\displaystyle{ \overrightarrow v }[/math] and therefore, the particle's momentum would increase in the direction of [math]\displaystyle{ \overrightarrow v }[/math]. In the light of this discussion, we define momentum flux as follows:

MOMENTUM FLUX

[math]\displaystyle{ \frac{\overrightarrow S}{c} = \frac{1}{\mu_0 c} \overrightarrow E \times \overrightarrow B }[/math]

The units of momentum flux would be [math]\displaystyle{ W.s/m^3 }[/math] or [math]\displaystyle{ J/m^3 }[/math] or [math]\displaystyle{ N.m/m^3 }[/math] which is [math]\displaystyle{ N/m^2 }[/math]. So the momentum flux has the same dimensions as pressure.

Now by the principle of conservation of momentum we know that if the radiation imparts momentum to a particle, it should lose an equal amount of momentum and therefore, the magnetic field should also be smaller in magnitude after an interaction with matter.

A Computational Model

In order to make computations using these concepts, simply make a list of the available information including all the physical quantities whose values are known and then also mention the physical quantity that you are looking to find. Then based on the given information, look for the best formula to apply from the ones mentioned earlier. Sometimes, the questions may not be as straightforward and in that case, we may need to manipulate some values to reach a form which contains the required information. Let's look at some examples to help us understand how to apply this knowledge to problem solving.

Examples

Simple/Medium

A small laser used as a pointer produces a beam of red light 5mm in diameter and has a power output of 5mW. What is the magnitude of the electric field in the laser beam?

Solution

Sol 1

Difficult

A 100 W light bulb is placed in a fixture with a reflector that makes a spot of radius 20 cm. Calculate approximately the amplitude of the radiative electric field in the spot.

Solution

Connectedness

How is this topic connected to something that you are interested in? Is there an interesting industrial application?

This concept is connected to the topic of building solar sails which is something that I am interested in and the concept of radiation pressure forms the basis of solar sails which is the industrial application for the same (let's discuss).

Solar sails (also called light sails or photon sails) are a form of spacecraft propulsion using the radiation pressure (also called solar pressure) from stars to push large ultra-thin mirrors to high speeds. Light sails could also be driven by energy beams to extend their range of operations, which is strictly beam sailing rather than solar sailing.

When electromagnetic radiation strikes the neutral matter, it causes a magnetic force on both the protons and electrons in the matter in the same direction i.e. the direction of propagation of the radiative pulse (referred to as radiation pressure). In spite of the fact that radiation pressure is a small effect, there have been some serious proposals to build spaceships with huge solar sails, many kilometers in diameter, that could move around the solar system because of the radiation pressure of sunlight on the sails. The effect is doubled if the sails are highly reflective and the plans call for sails made of very thin aluminized plastic.

Solar sail craft offer the possibility of low-cost operations combined with long operating lifetimes. Since they have few moving parts and use no propellant, they can potentially be used numerous times for delivery of payloads. Solar sails use a phenomenon that has a proven, measured effect on spacecraft. Solar pressure affects all spacecraft, whether in interplanetary space or in orbit around a planet or small body. A typical spacecraft going to Mars, for example, will be displaced by thousands of kilometers by solar pressure, so the effects must be accounted for in trajectory planning, which has been done since the time of the earliest interplanetary spacecraft of the 1960s. Solar pressure also affects the attitude of a craft, a factor that must be included in spacecraft design.

Another application is optical tweezers. Electromagnetic waves or photons transport energy and momentum. When an electromagnetic wave interacts with a small particle, it can exchange energy and momentum with the particle. The force exerted on the particle is equal to the momentum transferred per unit time. Optical tweezers use this force to provide a non-invasive technique for manipulating microscopic-sized particles with light. They have become an important tool for the life sciences to answer questions and generate knowledge of biological significance.

How is it connected to your major?

As a computer science major with an interest in aeronautical engineering, I am interested in writing software to drive the solar sails through the solar system and in order to write accurate and efficient programs for the same, the knowledge of the principles behind the working of solar sails would be really helpful. So the concepts of energy and momentum of electromagnetic radiation have proven to be really useful for my future pursuits.

History

Johannes Kepler put forward the concept of radiation pressure back in 1619 to explain the observation that a tail of a comet always points away from the Sun. The assertion that light, as electromagnetic radiation, has the property of momentum and thus exerts a pressure upon any surface exposed to it was published by James Clerk Maxwell in 1862, and proven experimentally by Russian physicist Pyotr Lebedev in 1900 and by Ernest Fox Nichols and Gordon Ferrie Hull in 1901. The pressure is very feeble, but can be detected by allowing the radiation to fall upon a delicately poised vane of reflective metal in a Nichols radiometer (this should not be confused with the Crookes radiometer, whose characteristic motion is not caused by radiation pressure but by impacting gas molecules).

In 1862-4 James Clerk Maxwell developed equations for the electromagnetic field which suggested that waves in the field would travel with a speed that was very close to the known speed of light. Maxwell therefore suggested that visible light (as well as invisible infrared and ultraviolet rays by inference) all consisted of propagating disturbances (or radiation) in the electromagnetic field.

Oliver Heaviside was a self-taught scholar who reformulated Maxwell's field equations in terms of electric and magnetic forces and energy flux, and independently co-formulated vector analysis. His series of articles continued the work entitled "Electromagnetic Induction and its Propagation", commenced in The Electrician in 1885 to nearly 1887 (ed., the latter part of the work dealing with the propagation of electromagnetic waves along wires through the dielectric surrounding them), when the great pressure on space and the want of readers appeared to necessitate its abrupt discontinuance. (A straggler piece appeared December 31, 1887.)

The last portion of the EM spectrum to be discovered was associated with radioactivity. Henri Becquerel found that uranium salts caused fogging of an unexposed photographic plate through a covering paper in a manner similar to X-rays, and Marie Curie discovered that only certain elements gave off these rays of energy, soon discovering the intense radiation of radium. The radiation from pitchblende was differentiated into alpha rays (alpha particles) and beta rays (beta particles) by Ernest Rutherford through simple experimentation in 1899, but these proved to be charged particulate types of radiation. However, in 1900 the French scientist Paul Villard discovered a third neutrally charged and especially penetrating type of radiation from radium, and after he described it, Rutherford realized it must be yet a third type of radiation, which in 1903 Rutherford named gamma rays. In 1910 British physicist William Henry Bragg demonstrated that gamma rays are electromagnetic radiation, not particles, and in 1914 Rutherford and Edward Andrade measured their wavelengths, finding that they were similar to X-rays but with shorter wavelengths and higher frequency, although a 'cross-over' between X and gamma rays makes it possible to have X-rays with a higher energy (and hence shorter wavelength) than gamma rays and vice versa. The origin of the ray differentiates them, gamma rays tend to be a natural phenomena originating from the unstable nucleus of an atom and X-rays are electrically generated (and hence man-made) unless they are as a result of bremsstrahlung X-radiation caused by the interaction of fast moving particles (such as beta particles) colliding with certain materials, usually of higher atomic numbers.

https://en.wikipedia.org/wiki/Electromagnetic_radiation#History_of_discovery

http://labman.phys.utk.edu/phys222core/modules/m6/wave_energy_and_momentum.htm