Combining Electric and Magnetic Forces

Claimed by Alana Kaplan (Fall, 2015); Claimed to Edit by Alexis Jacob (Spring, 2016 - Added middle and difficult examples, figures, and minor format changes) Claimed by Ha Eun An (Fall 2016)

Though the pattern in which electric and magnetic forces interact with particles is observably different, their effects can be quantitatively be compared. The principle of adding the two functions of force as a net force is one that now serves as a fundamental principle of electromagnetics. It serves as a building block for many important Laws such as Hall Effect and Motional Emf.

The Main Idea

If a charged particle within an electric field is moving in a magnetic field, the particle is subject to an Electric Force and a Magnetic Force. The net force on the particle is called the Lorentz Force, which is the sum of electric and magnetic forces.

A Mathematical Model

Electric Forces

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 1. An electric force acts in a pattern parallel to the electric field, pointing radially inward or outward of a particle. The direction depends on the signs of the interacting charged particles.

• A particle being acted upon by an electric force will move in a straight line, in the path, or negative path depending on charge, of the the electric field line (See Figure 1) .

• Electric fields point in a direction radially outward/ inward of a charged particle. There are four possible scenarios for the interaction of 2 charged particles:

1. A negatively charged particle (p1) is acting on a negatively charged particle (p2)

- p2 feels force pointing radially outward from p2

2. A positively charged particle (p1) is acting on a negatively charged particle (p2)

- p2 feels force pointing radially inward toward p2

3. A negatively charged particle (p1) is acting on a positively charged particle (p2)

- p2 feels force pointing radially inward toward p1

4. A positively charged particle (p1) is acting on a positively charged particle (p2)

- p2 feels force pointing radially outward from p1

• The electric force formula: [math]\displaystyle{ \vec {F}_{E}=q\vec E }[/math]

- Force on the observed particle is determined by the interaction of the charge of the observed particle and the electric field created by other charged particles.

Magnetic Forces

**Figure 2.** Magnetic Fields follow a helical pattern

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 3. Magnetic Force Right Hand Rule

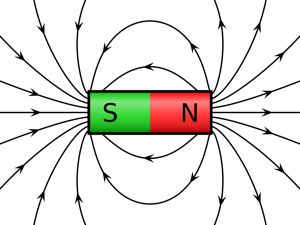
• The magnetic force on a charged particle is orthogonal to the magnetic field.

• The particle must be moving with some velocity for a magnetic force to be present.

• Particles move perpendicular to the magnetic field lines in a helical manner (See Figure 2)

• To find the magnetic force, you can use the Right Hand Rule as follows (See Figure 3):

1. Thumb in direction of the velocity

2. Fingers in the direction of the magnetic field

3. Your palm will face in the direction of the Magnetic Force

• The magnetic force formula: [math]\displaystyle{ {\vec {F}_{M} = q\vec {v}\times\vec {B}} }[/math]

- q is the charge of the moving charge, including its sign

- [math]\displaystyle{ \vec v }[/math] is the velocity of the moving charge

- [math]\displaystyle{ \vec B }[/math] is the applied magnetic field, in Tesla

- Note: if [math]\displaystyle{ \vec v }[/math] and [math]\displaystyle{ \vec B }[/math] are parallel to each other, [math]\displaystyle{ {\vec {F}_{M} = 0} }[/math] ([math]\displaystyle{ {\vec {A}\times\vec {B} = |\vec A||\vec B|sin(θ) = 0} }[/math])

Electric and Magnetic Forces Combined

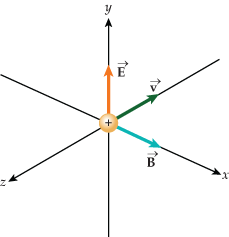
**Figure 4.** The electric field, magnetic field, and velocity vector are all perpendicular to each other

• The Lorentz Force formula:

[math]\displaystyle{ {\vec {F}_{net} = \vec {F}_{E} + \vec {F}_{M}} }[/math]

[math]\displaystyle{ {\vec {F}_{net} = q\vec E + q\vec {v}\times\vec {B}} }[/math]

• When the net force is equal to zero, the velocity stays constant.

[math]\displaystyle{ {\vec {F}_{E} = \vec {F}_{M}} }[/math]

[math]\displaystyle{ {q\vec E = q\vec {v}\times\vec {B}} }[/math]

As seen in Figure 4 , when the net forces acting on a particle are balanced the electric field, magnetic field, and velocity vector are all perpendicular to each other. The electric and magnetic forces are equal but opposite. When forces are not balanced the trajectory of the the particle will change.

The Lorentz Force calculation is now a fundamental principle of electromagnetism.

Examples

Simple

Example 1:

A proton is moving with velocity 7e8 in the +x direction. The trajectory of the proton is constant. There is an electric field in the area of 3.6e7 in the +y direction. Calculate the direction and magnitude of the magnetic field acting on the particle?

Solution:

Step 1: [math]\displaystyle{ {|q\vec E| = |q\vec v\vec B|} }[/math]

Step 2: [math]\displaystyle{ {\vec {E} = \vec {v}\vec {B}} }[/math]

Step 3: [math]\displaystyle{ {\vec {B} = \frac {\vec {E}} {\vec {v}} = \frac {3.6e7} {7e8}} }[/math]

Answer: [math]\displaystyle{ {\vec {B} = 0.051 T} }[/math]

The magnetic field is in the +z direction.

Middling

Example 1:

At a particular instant, a proton is moving with velocity <0,5e5,0> m/s and an electron is moving with velocity <-4.2e2,0,0> m/s. The electron is located 1.4e-3 m below the proton (in the -y direction). Determine the net force on the electron due to the proton.

Solution:

Step 1: [math]\displaystyle{ {\vec {F}_{net} = \vec {F}_{E} + \vec {F}_{B}} }[/math]

Step 2: [math]\displaystyle{ {\vec {F}_{net} = \vec {F}_{E} + 0 = q\vec {E}} }[/math] (At the electron's location, [math]\displaystyle{ \vec B = 0 }[/math] because the velocity of the proton is parallel to [math]\displaystyle{ \hat{r} }[/math])

Step 3: [math]\displaystyle{ {\vec {E} = \frac {1} {4πεo} \frac {q} {r^2} \hat{r}} }[/math] ([math]\displaystyle{ \hat{r} = \lt 0,-1,0\gt and r = 1.4e-3 m }[/math])

Step 4: [math]\displaystyle{ \vec E = \lt 0,-7.35e-4,0\gt N/C }[/math]

Step 5: [math]\displaystyle{ {\vec {F}_{net} = -e \vec E = \lt 0,1.18e-22,0\gt N} }[/math]

Difficult

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 5. Middle example diagram.

Q: A copper bar of length L and zero resistance slides at a constant velocity, v. There is a uniform magnetic field, B, directed into the page. A voltmeter is connected across a resistor, R, and reads ΔV. See Figure 5.

Determine the direction of the magnetic force on the diagram and the current through the resistor. Your answer should be in terms of the given variables.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 6. Middle example solution.

A: Direction of the Magnetic Force- Use right hand rule for v cross B. See Figure 6.

Current through the resistor-

ΔV round trip = 0

ΔV round trip = +motional emf - ΔV resistor = 0

motional emf = IR

I = (motional emf/R)

According to Lorentz force, |F(e)| = |F(B)|

q*E = q*v*B

E = v*B

|ΔV| = E*ΔL = vBL

I = (vBL)/R

Connectedness

The Lorentz Force principle has been a component in many modern day inventions and critical building block for many physics principles. With known forces, we can predict the very important figure, the velocity and trajectory of a moving particle.

Applications

Velocity Selector

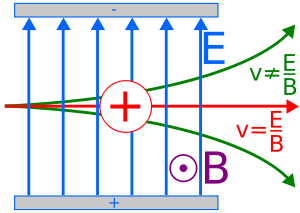
The Velocity Selector is a device used to filter particles based on their velocity. A Velocity Selector uses controlled, perpendicular, electric and magnetic fields to filter certain charged particles (See Figure 7 ). Particles with the correct speed will be unaffected while other particles will be deflected. This technique is used in technologies such as electron microscopes and spectrometers.

Electric Motor

An electric motor is a device that uses the Lorentz force to convert electric energy into mechanical energy. Using the magnetic torque principle, electric energy is created by using the magnetic field of a magnet. The torque laws are based off the principles of the net electric and magnetic forces.

All images found on google image search: https://en.wikipedia.org/wiki/Magnetic_field https://en.wikipedia.org/wiki/Wien_filter http://aplusphysics.com/wordpress/regents/em/electric-field/

Fields

Combining Electric and Magnetic Forces

Contents

The Main Idea

A Mathematical Model

Electric Forces

Magnetic Forces

Electric and Magnetic Forces Combined

Examples

Simple

Middling

Difficult

Connectedness

Applications

Other related topics

See also

Further reading

External links

References

Navigation menu