Relative Velocity
Claimed by Lily Masters (Fall 2016)
Edited by Raj Patel (Spring 2017)
The motion of an object looks different based on the line of sight. This is known as a reference frame.
Relative Velocity
When an object is moving in a medium that is also moving, its velocity may be different depending on the location of the observer. For example, consider a boat moving through a flowing river. If the observer is aboard the boat, the velocity will be different than if the observer was standing by the side of the river. This can be more easily described through vector addition with one reference frame considered an intermediate reference frame:
[math]\displaystyle{ \vec{v}_{AC} = \vec{v}_{AB} + \vec{v}_{BC} }[/math]
This means that the velocity of A with respect to C is equal to the sum of the velocity of A with respect to B and the velocity of B with respect to C. In this case, B is the intermediate reference frame.
Examples
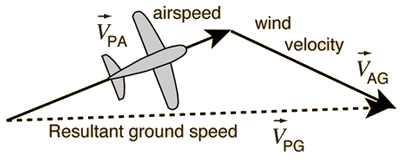
Airplane in Wind
An airplane is flying with a velocity of [math]\displaystyle{ \vec{v}_{PA} }[/math] relative to the air. The wind is moving with a velocity of [math]\displaystyle{ \vec{v}_{AG} }[/math] relative to an observer on the ground. The velocity of the plane relative to the ground can be found using vector addition:
[math]\displaystyle{ \vec{v}_{PG} = \vec{v}_{PA} + \vec{v}_{AG} }[/math]
Suppose the plane is moving with a velocity of [math]\displaystyle{ \left \langle {150,20,0} \right \rangle }[/math] km/h relative to the air. The wind is moving with a velocity of [math]\displaystyle{ \left \langle {-25,0,-10} \right \rangle }[/math] km/h relative to the ground. What is the velocity of the plane relative to the ground?
Answer:
[math]\displaystyle{ \vec{v}_{PG} = \left \langle {150,20,0} \right \rangle + \left \langle {-25,0,-10} \right \rangle }[/math]
[math]\displaystyle{ \vec{v}_{PG} = \left \langle {125,20,-10} \right \rangle }[/math]
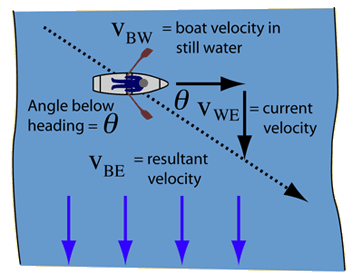
Boat in Current
A boat is moving straight across a river with a velocity of [math]\displaystyle{ \vec{v}_{BW} }[/math] relative to the water. The river has a current flowing perpendicular to the boat which has a velocity of [math]\displaystyle{ \vec{v}_{WE} }[/math] relative to the earth. The velocity of the boat relative to the Earth can be found using vector addition and the bearing of the boat can be found using trig relations:
[math]\displaystyle{ \vec{v}_{BE} = \vec{v}_{BW} + \vec{v}_{WE} }[/math]
[math]\displaystyle{ \Theta = \arctan \frac{\left \Vert \vec{v}_{WE} \right \|}{\left \Vert \vec{v}_{BW} \right \|} }[/math]
Suppose the boat is moving straight across the river with a velocity of 37 m/s relative to the water and the current is moving downstream and perpendicular to the boat with a velocity of 4 m/s relative to the earth. What is the velocity of the boat relative to the earth and what is its bearing?
Answer:
[math]\displaystyle{ \vec{v}_{BE} = \left \langle {37,0,0} \right \rangle + \left \langle {0,-4,0} \right \rangle }[/math]
[math]\displaystyle{ \vec{v}_{BE} = \left \langle {37,-4,0} \right \rangle }[/math]
[math]\displaystyle{ \Theta = \arctan \frac{4}{37} }[/math]
[math]\displaystyle{ \Theta = 6.17018^\circ }[/math]
See also
External links