Potential Difference of Point Charge in a Non-Uniform Field
Claimed by dmengesha3 Dina Claimed by Qianyi Qu Spring 2017
The Main Idea
Non uniform electric fields are generated by point charges because the magnitude is different depending on the location at which the electric field is being observed (refer to the equation of the electric field made by a point charge). If one is trying to find the electric potential between two different locations due to a point charge the difference in electric fields at those two points must be considered. The potential difference in non-uniform electric fields can be calculated by adding up the contribution of potential difference of each individual electric field through certain distance we want to evaluate. Generally, in a non-uniform electric field one can write the change in potential difference between two locations to be: [math]\displaystyle{ {\triangle V}=-\int\limits_{i}^{f} \vec{E} {\bullet} \vec{l} }[/math] with being the initial location and f being the final location. And the sum of all the contribution of potential difference can be written as: [math]\displaystyle{ {\triangle V}=-\sum \vec{E} {\bullet} \triangle\vec{l} }[/math]. The electric field of the object can be that of a point charge, long rod, disk, capacitor, or sphere. Ideally, these equation can be used to calculate potential difference along curve path and situations where the electric field varies in magnitude and direction with respect to distance traveled. For the simplicity of calculation, we will only consider cases with varying electric field on a straight path in this class.
A Mathematical Model
Steps to calculate Potential Difference in a Non-Uniform Field:
1. Pick a path from initial to final location where the electric field can be evaluated at every location.
2. Divide the path into smaller pieces, with each pieces having its unique electric field and [math]\displaystyle{ \vec{l} }[/math].
3. Identify the electric field of the piece.
4. Use the integral equation for potential difference shown above to calculate the potential difference of one piece.
5. Move on to calculate the next piece.
6. Add contribution of all pieces together to get the net potential difference in non-uniform field.
For example, we substitute E for the formula for the electric field of a point charge and dl for r the distance between the point charge and the observation location.
[math]\displaystyle{ \textstyle\int\limits_{i}^{f}(9x10^9)\frac{Q}{r^2}dr }[/math]
If we carry out the integration we find that Vf- Vi = [math]\displaystyle{ \vartriangle(9x10^9)\frac{Q}{r} }[/math] which can also be written [math]\displaystyle{ ((9x10^9)\frac{Q}{rf})-((9x10^9)\frac{Q}{ri}) }[/math]
This equation can be used to determine the potential difference of a point charge between any two different locations.
A Computational Model
Refer to this Website:
https://phet.colorado.edu/sims/charges-and-fields/charges-and-fields_en.html
To observe how the electric field of a point charge differs from one location to another because it is proportional to 1/r^2. Then play around with measuring the potential difference between two points and see how distance affects the calculation of potential difference. You should observe a 1/r relationship.
Exercises 1. Put down a positive charge. Put 3 E-Field Sensors down: one close to the charge, the next farther away, the next one even farther still
Notice that the magnitude of the arrows decreases as the distance from the point charge increases
2. Repeat the steps of #1 but replace the positive point charge with a negative point charge.
You should notice the same trend occur
3. Click "Show E-field" on the right menu bar and move the point charge around the plot
Notice that the Electric field gets larger in magnitude as the point charge moves closer to the observation location
4. Move the point charge closer to the observation location that measures potential difference
Notice that the closer the point charge is to this location the higher the magnitude of the potential difference
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple

1) If the path is along the line i to f what direction is the electric field of the dipole?
down
up
left
right
Cannot determine
Answer:
To the left. The electric field would point toward the negative end of the dipole
Is the potential difference Vf-Vi
positive
negative
zero
Answer:
It is negative because both deltal (displacement) and Electric field are pointing in the same direction which means that their product would have been positive and the negative sign in front of the expression -Edl would make the answer negative.
Shortcut to remember: E and dl same direction --> negative potential difference E and dl opposite direction-->positive potential difference
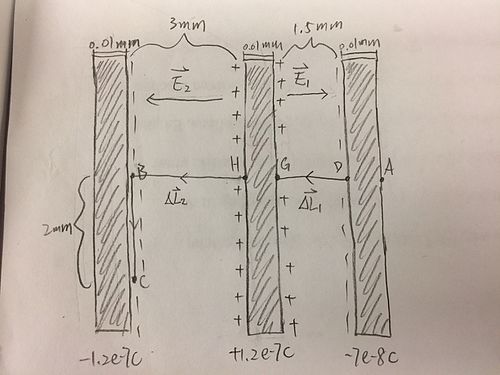
2) Three charged metal disks are arranged as shown on the right. The disks are held apart by insulating supports not shown in the diagram. Each disk has an area of 2[math]\displaystyle{ m^2 }[/math] (this is the area of one side of the disk). Calculate the potential difference Vd-Va.
Answer:
Path: A [math]\displaystyle{ \rightarrow }[/math] D [math]\displaystyle{ \rightarrow }[/math] G [math]\displaystyle{ \rightarrow }[/math] H [math]\displaystyle{ \rightarrow }[/math] B [math]\displaystyle{ \rightarrow }[/math] C
Vd-Va and Vh-Vg are zero because E=0 in a metal. Vc-Vb is also zero because the path the perpendicular to [math]\displaystyle{ \vec{E_2} }[/math].
Update Path: A [math]\displaystyle{ \rightarrow }[/math] B [math]\displaystyle{ \rightarrow }[/math] C
Electric Field of Capacitors: [math]\displaystyle{ E_{cap} = \frac{Q}{A\epsilon_0} }[/math]
Vc-Va = (Vb-Vh) + (Vg-Vd) = [math]\displaystyle{ -\vec{E_2} \bullet \triangle\vec{L_2} - \vec{E_1} \bullet \triangle\vec{L_1} }[/math]
= [math]\displaystyle{ -\frac{1.2e-7C*0.003m}{2m^2*8.85e-12 C^2/Nm^2} }[/math] + [math]\displaystyle{ -\frac{7e-8C*0.0015m}{2m^2*8.85e-12 C^2/Nm^2} }[/math]
= 14.4 V
Middling
3) Calculate the change in potential moving from location [math]\displaystyle{ (9x10^-9) m }[/math] to location [math]\displaystyle{ (9.7x10^-9) m }[/math] from a proton.
Answer:
the final location is: (9.7x10^-9) m
the intial location is: (9x10^-9) m
So if we plug these values into the above equation we found by integrating Edr.
We have: [math]\displaystyle{ ((9x10^9)\frac{1.6x10^-19}{9.7x10^-9})-((9x10^9)\frac{1.6x10^-19}{9x10^-9}) }[/math]
Which yields a potential difference of -0.0115 V.

4) A very long, thin glass rod of length 2R carries a uniformly distributed charge +q. A very large plastic disk of radius R, carrying a uniformly distributed charge -Q, is located a distance d from the rod, where d<<R.
a. Predict the sign of the potential difference Vc-Va. Justify your answer.
Answer:
E and dl are both positive because they point to the right direction. According to the integral form of the potential difference formula for non-uniform field, [math]\displaystyle{ {\triangle V}=-\int\limits_{i}^{f} \vec{E} {\bullet} \vec{l} }[/math] , the change in V from position A to C has to be negative.
b. Calculate the potential difference Vc-Va. Location A is located a distance w fro the center of the rod. Location C is located at the disk's center a distance d from the rod.
Answer:
Assume d<<R. [math]\displaystyle{ E_{disk} = \frac{Q}{2A\epsilon_0} }[/math] & [math]\displaystyle{ E_{rod} = \frac{1}{4\pi\epsilon_0} }[/math] [math]\displaystyle{ \frac{2Q}{Lr} }[/math]
Vc-Va = [math]\displaystyle{ {\triangle V}=-\int\limits_{i}^{f} \vec{E_{net}} {\bullet} \vec{l} }[/math] = [math]\displaystyle{ \triangle {V_{rod}} + \triangle {V_{disk}} }[/math]= [math]\displaystyle{ -\int\limits_{i}^{f} \vec{E_{rod}} {\bullet} \vec{l} }[/math] [math]\displaystyle{ -\int\limits_{i}^{f} \vec{E_{disk}} {\bullet} \vec{l} }[/math]
[math]\displaystyle{ {\triangle V_{rod}}=-\int\limits_{w}^{d} \frac{1}{4\pi\epsilon_0} }[/math][math]\displaystyle{ \frac{2q}{xL} dx }[/math] = [math]\displaystyle{ \frac{-2q}{4\pi\epsilon_0L} [ln(x)\rbrack^d_w }[/math] = [math]\displaystyle{ \frac{-2q}{4\pi\epsilon_0L} ln(\frac{d}{w}) }[/math]
[math]\displaystyle{ {\triangle V_{disk}}=-\int\limits_{w}^{d} \frac{Q}{2A\epsilon_0} dx }[/math]= [math]\displaystyle{ \frac{-Q}{2A\epsilon_0} [x\rbrack^d_w }[/math] = [math]\displaystyle{ \frac{-Q}{2A\epsilon_0L} (d-w) }[/math]
Vc-Va = -[math]\displaystyle{ [\frac{2q}{4\pi\epsilon_0L} ln(\frac{d}{w}) }[/math] + [math]\displaystyle{ \frac{Q}{2A\epsilon_0L} (d-w)] }[/math]
Difficult
5) The potential calculated for a point charge in a particular region of space is written by V=14xy+6y-4z, what are the electric field components at location <x,y,z>?
Answer:
Remember that potential difference [math]\displaystyle{ \textstyle\int\limits_{i}^{f}-Edl }[/math] thus Electric field can be calculated as the [math]\displaystyle{ \frac {-dv}{dx} }[/math] So one would take the derivative of the potential difference with respect to each variable giving:
E= <-14y,-14x-6,4>
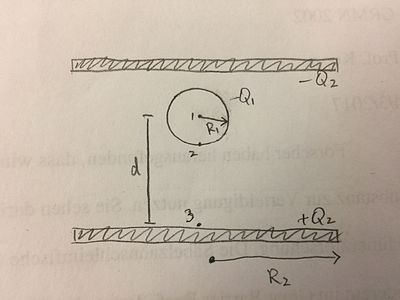
6) The diagram shows a spherical shell with a uniformed surface charge of -Q and a capacitor with uniformed distributed +Q2 and -Q2. R1<<R2, d<<R2. Calculate the potential difference V2-V1 and V3-V2.
Answer:
V2-V1:
[math]\displaystyle{ E_{sphere} =0 }[/math] inside the sphere, so the only electric field acting along this distance is [math]\displaystyle{ E_{cap} }[/math]. [math]\displaystyle{ E_{cap} = \frac{Q_2}{A\epsilon_0} }[/math]
[math]\displaystyle{ \triangle V_{cap} = V_2-V_1 = -\int\limits_{0}^{-R_1} \frac{Q_2}{2A\epsilon_0} dy }[/math] = [math]\displaystyle{ \frac{-Q}{\pi\epsilon_o} [x\rbrack_0^{-R_1} = \frac{Q_2R_1}{\pi{R_1^2}\epsilon_0} }[/math]
V3-V2:
The net electric field is due to the sphere and the capacitor. [math]\displaystyle{ E_{sphere} = -\frac{1}{4\pi\epsilon_0} \frac{Q}{y^2} }[/math]
[math]\displaystyle{ \triangle V_{sphere} = -\int\limits_{d}^{R_1} \frac{1}{4\pi\epsilon_0} \frac{Q}{y^2} dy }[/math] = [math]\displaystyle{ -\frac{Q}{4\pi\epsilon_0} [\frac{1}{y}\rbrack_d^{R_1} }[/math] = [math]\displaystyle{ -\frac{Q}{4\pi\epsilon_0} (\frac{1}{R_1} - \frac{1}{d}) }[/math]
[math]\displaystyle{ \triangle V_{cap} = -\int\limits_{R_1}^{d} \frac{Q}{A\epsilon_0} dy }[/math] = [math]\displaystyle{ -\frac{Q}{A\epsilon_0} (d-R_1) = -\frac{Q}{\pi{R_2^2}\epsilon_0} (d-R_1) }[/math]
[math]\displaystyle{ \triangle V_{sphere}+\triangle V_{cap} = V_3-V_2 = -\frac{Q}{4\pi\epsilon_0} (\frac{1}{R_1} - \frac{1}{d}) -\frac{Q}{\pi{R_2^2}\epsilon_0} (d-R_1) }[/math]
Connectedness
How is this connected to something you are interested in?
Connections in Chemistry
Electrostatic potential energy maps are made of molecules to portray the charge distribution of a molecule 3 dimensionally. These maps can be used to determine electronegativity, bond characteristics, and also help find the reactive sites of molecules. Reactive sites are defined as a charged region of a molecule that interact with other charged particles. This can become especially important in assessing what types of molecular interactions and reactions will take place between two elements or compounds.
How is it connected to your major?
I am a Biology major here at Tech. In biochemistry we use the principle of potential energies of half reactions to calculate the standard free energy [math]\displaystyle{ \vartriangle G }[/math] of a reaction in order to understand the reaction's energetics and determine whether the reaction is favorable or not. This predictive information allows biologists to know what chemical reactions take place in the body and which are able to take place in the body.
Industrial Application
Coulomb Barrier for Nuclear Fusion: For two particles (ex: 2 protons to fuse), they must be able to get close enough to one another for the nuclear strong force to overcome their electric repulsion. One must understand the potential difference of a point charge and the potential energy that creates a barrier between two point charges which can be calculated using U=ke^2/r where k =9e9 and e=1.6e-19 The r calculated using this formula determines the radius at which the nuclear attractive force becomes dominant.
History
In 1800, Alessandro Volta (pictured above) found that metals such as zinc and copper could produce currents; thus, he constructed the first battery what is know called a voltic pile. It was constructed from pieces of zinc and copper in salt water which produced an electric current. The SI unit for potential difference is named after Alessandro Volta.
Refer to:
https://en.wikipedia.org/wiki/Alessandro_Volta
To read more about Volta's early works and life.
See also
Calculating Electric Field of a Point Charge
http://www.physicsbook.gatech.edu/Point_Charge
Potential Difference in Uniform Electric Field
http://www.physicsbook.gatech.edu/Potential_Difference_in_a_Uniform_Field
Further reading
Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions: Electric and Magnetic Interactions. 4th ed. Vol. II. Place of Publication Not Identified: John Wiley, 2015. Print. Chapter 16. Section 16.5
External links
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/potpoi.html
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/mulpoi.html
References
http://hyperphysics.phy-astr.gsu.edu/hbase/nucene/coubar.html#c1
https://en.wikipedia.org/wiki/Volt
http://content.time.com/time/specials/2007/article/0,28804,1677329_1677708_1677755,00.html
