Main Page: Difference between revisions

Revision as of 00:58, 17 April 2016

Welcome to the Georgia Tech Wiki for Introductory Physics. This resource was created so that students can contribute and curate content to help those with limited or no access to a textbook. When reading this website, please correct any errors you may come across. If you read something that isn't clear, please consider revising it for future students!

Looking to make a contribution?

Pick one of the topics from intro physics listed below
Add content to that topic or improve the quality of what is already there.
Need to make a new topic? Edit this page and add it to the list under the appropriate category. Then copy and paste the default Template into your new page and start editing.

Please remember that this is not a textbook and you are not limited to expressing your ideas with only text and equations. Whenever possible embed: pictures, videos, diagrams, simulations, computational models (e.g. Glowscript), and whatever content you think makes learning physics easier for other students.

Source Material

All of the content added to this resource must be in the public domain or similar free resource. If you are unsure about a source, contact the original author for permission. That said, there is a surprisingly large amount of introductory physics content scattered across the web. Here is an incomplete list of intro physics resources (please update as needed).

A physics resource written by experts for an expert audience Physics Portal
A wiki written for students by a physics expert MSU Physics Wiki
A wiki book on modern physics Modern Physics Wiki
The MIT open courseware for intro physics MITOCW Wiki
An online concept map of intro physics HyperPhysics
Interactive physics simulations PhET
OpenStax algebra based intro physics textbook College Physics
The Open Source Physics project is a collection of online physics resources OSP
A resource guide compiled by the AAPT for educators ComPADRE

Organizing Categories

These are the broad, overarching categories, that we cover in three semester of introductory physics. You can add subcategories as needed but a single topic should direct readers to a page in one of these categories.

Resources

Commonly used wiki commands Wiki Cheatsheet
A guide to representing equations in math mode Wiki Math Mode
A page to keep track of all the physics Constants
A page for review of Vectors and vector operations
A listing of Notable Scientist with links to their individual pages

Physics 1

Week 1

Student Content

Help with VPython

Vectors and Units

Interactions

Types of Interactions and How to Detect Them

Velocity and Momentum

Expert Content

Software for Projects

Week 2

Student Content

Momentum and the Momentum Principle

Iterative Prediction with a Constant Force

Expert Content

Week 3

Student Content

Analytic Prediction with a Constant Force

Analytical Prediction

Iterative Prediction with a Varying Force

Expert Content

Week 4

Student Content

Fundamental Interactions

Expert Content

Non-constant Force: Newtonian Gravitation

Week 5

Student Content

Conservation of Momentum

Conservation of Momentum

Properties of Matter

Expert Content

Modeling a Solid Wire: springs in series and parallel

Week 6

Student Content

Identifying Forces

Curving Motion

Expert Content

Week 7

Student Content

Energy Principle

Expert Content

Week 8

Student Content

Work by Non-Constant Forces

Work Done By A Nonconstant Force

Potential Energy

Expert Content

Week 9

Student Content

Multiparticle Systems

Expert Content

Week 10

Student Content

Choice of System

System & Surroundings

Thermal Energy, Dissipation and Transfer of Energy

Rotational and Vibrational Energy

Translational, Rotational and Vibrational Energy

Expert Content

Week 11

Student Content

Different Models of a System

Models of Friction

Expert Content

Week 12

Student Content

Collisions

Expert Content

Week 13

Student Content

Rotations

Angular Momentum

Expert Content

Week 14

Student Content

Analyzing Motion with and without Torque

Expert Content

Week 15

Student Content

Introduction to Quantum Concepts

Expert Content

Discovery of the Nucleus

Physics 2

Week 1

3D Vectors

CLAIMED BY DIPRO CHAKRABORTY

CLAIMED BY DIPRO CHAKRABORTY CLAIMED BY DIPRO CHAKRABORTY CLAIMED BY DIPRO CHAKRABORTY

CLAIMED BY DIPRO CHAKRABORTY

Electric field

The electric field created by a charge is present throughout space at all times, whether or not there is another charge around to feel its effects. The electric field created by a charge penetrates through matter. The field permeates the neighboring space, biding its time until it can affect anything brought into its space of interaction.

The Main Idea

To be exact, the definition of the Electric Field is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other objects.

If we put a charged particle at a location and it experiences a force, it would be logical to assume that there is something present that is interacting with the particle. This "virtual force" is in essence the electric field.

A Mathematical Model

The electric field can be expressed mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

[math]\displaystyle{ {\vec{F_{2}} = {q_{1}}{\vec{E_{1}}} \Leftrightarrow \frac{d\vec{v}}{dt}} }[/math]

which can be translated to postulate that the force on particle 2 is determined by the charge of particle 2 and the electric field.

Examples

The following examples are to test your basic understanding of the Electric Field. For more examples that test your knowledge of all three of the laws, peruse the class textbook.

Simple

Which way is the electric field going for a negatively charged particle?

It's easy to see that the electric field is pointing toward the negatively charged particle. The electric field is tending toward the negatively charged particle.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the Electric Field is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other objects.

If we put a charged particle at a location and it experiences a force, it would be logical to assume that there is something present that is interacting with the particle. This "virtual force" is in essence the electric field.

A Mathematical Model

The electric field can be expressed mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

[math]\displaystyle{ {\vec{F_{2}} = {q_{1}}{\vec{E_{1}}} \Leftrightarrow \frac{d\vec{v}}{dt}} }[/math]

which can be translated to postulate that the force on particle 2 is determined by the charge of particle 2 and the electric field.

Examples

The following examples are to test your basic understanding of the Electric Field. For more examples that test your knowledge of all three of the laws, peruse the class textbook.

Simple

Which way is the electric field going for a negatively charged particle?

It's easy to see that the electric field is pointing toward the negatively charged particle. The electric field is tending toward the negatively charged particle.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the Electric Field is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other objects.

If we put a charged particle at a location and it experiences a force, it would be logical to assume that there is something present that is interacting with the particle. This "virtual force" is in essence the electric field.

A Mathematical Model

The electric field can be expressed mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

[math]\displaystyle{ {\vec{F_{2}} = {q_{1}}{\vec{E_{1}}} \Leftrightarrow \frac{d\vec{v}}{dt}} }[/math]

which can be translated to postulate that the force on particle 2 is determined by the charge of particle 2 and the electric field.

Examples

The following examples are to test your basic understanding of the Electric Field. For more examples that test your knowledge of all three of the laws, peruse the class textbook.

Simple

Which way is the electric field going for a negatively charged particle?

It's easy to see that the electric field is pointing toward the negatively charged particle. The electric field is tending toward the negatively charged particle.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the Electric Field is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other objects.

If we put a charged particle at a location and it experiences a force, it would be logical to assume that there is something present that is interacting with the particle. This "virtual force" is in essence the electric field.

A Mathematical Model

The electric field can be expressed mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

[math]\displaystyle{ {\vec{F_{2}} = {q_{1}}{\vec{E_{1}}} \Leftrightarrow \frac{d\vec{v}}{dt}} }[/math]

which can be translated to postulate that the force on particle 2 is determined by the charge of particle 2 and the electric field.

Examples

The following examples are to test your basic understanding of the Electric Field. For more examples that test your knowledge of all three of the laws, peruse the class textbook.

Simple

Which way is the electric field going for a negatively charged particle?

It's easy to see that the electric field is pointing toward the negatively charged particle. The electric field is tending toward the negatively charged particle.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the Electric Field is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other objects.

If we put a charged particle at a location and it experiences a force, it would be logical to assume that there is something present that is interacting with the particle. This "virtual force" is in essence the electric field.

A Mathematical Model

The electric field can be expressed mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

[math]\displaystyle{ {\vec{F_{2}} = {q_{1}}{\vec{E_{1}}} \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

which can be translated to postulate that the force on particle 2 is determined by the charge of particle 2 and the electric field.

Examples

The following examples are to test your basic understanding of the Electric Field. For more examples that test your knowledge of all three of the laws, peruse the class textbook.

Simple

Which way is the electric field going for a negatively charged particle?

It's easy to see that the electric field is pointing toward the negatively charged particle. The electric field is tending toward the negatively charged particle.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the Electric Field is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other charged particles or objects.

If we put a charged particle at a location and it experiences a force, it would be logical to assume that there is something present that is interacting with the particle. This "virtual force" is in essence the electric field.

A Mathematical Model

The electric field can be expressed mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

[math]\displaystyle{ {\vec{F_{2}} = {q_{1}}{\vec{E_{1}}} \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

which can be translated to postulate that the force on particle 2 is determined by the charge of particle 2 and the electric field.

Examples

The following examples are to test your basic understanding of Newton's First Law. For more examples that test your knowledge of all three of the laws, click .

Simple

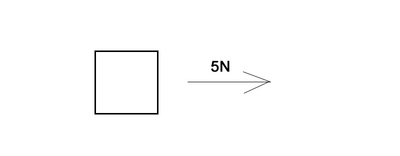
Does the object in the following image have a net force of zero? Does it have a constant velocity?

It's easy to see that the only force on the object is acting in the +x direction, with a magnitude of 5 newtons. Therefore, the object does not have a net force of zero or a constant velocity. It will be accelerating in the +x direction.

Middling

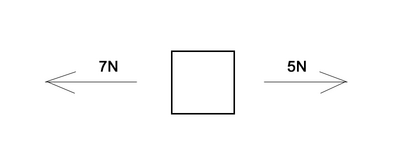
Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

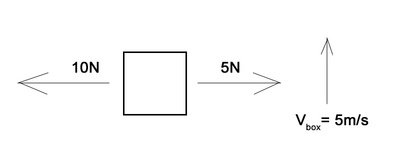
Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the First Law of Motion is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other charged particles or objects.

In other (and much simpler) terms, it means that an object at rest stays at rest and an object in in motion stays in motion at a constant velocity unless acted on by an unbalanced net force. It's important to keep in mind that only a difference in affect the velocity of an object. The amount of change in velocity is determined by

A Mathematical Model

Newton's first law can be stated mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

Where...

[math]\displaystyle{ \vec{F_{net}} }[/math] is the net force from the surroundings.

[math]\displaystyle{ d\vec{v} }[/math] is the change in velocity of the system.

[math]\displaystyle{ dt }[/math] is the change in time of the system

If we trace this formula from the left to the right, we can see that if the net force on an object is zero, then the change in velocity of an object is also zero. Conversely, if we were given an object and told that its change in momentum is zero, then we can deduce that the net force acting on the object is also zero. Keep in mind, however, that this formula simple deals with the change in velocity. It does not mean that the object is at rest, only that its velocity remains constant.

Examples

The following examples are to test your basic understanding of Newton's First Law. For more examples that test your knowledge of all three of the laws, click .

Simple

Does the object in the following image have a net force of zero? Does it have a constant velocity?

It's easy to see that the only force on the object is acting in the +x direction, with a magnitude of 5 newtons. Therefore, the object does not have a net force of zero or a constant velocity. It will be accelerating in the +x direction.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the First Law of Motion is as follows:

The electric field is a region around a charged particle or object within which a force would be exerted on other charged particles or objects.

In other (and much simpler) terms, it means that an object at rest stays at rest and an object in in motion stays in motion at a constant velocity unless acted on by an unbalanced net force. It's important to keep in mind that only a difference in affect the velocity of an object. The amount of change in velocity is determined by

A Mathematical Model

Newton's first law can be stated mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

Where...

[math]\displaystyle{ \vec{F_{net}} }[/math] is the net force from the surroundings.

[math]\displaystyle{ d\vec{v} }[/math] is the change in velocity of the system.

[math]\displaystyle{ dt }[/math] is the change in time of the system

If we trace this formula from the left to the right, we can see that if the net force on an object is zero, then the change in velocity of an object is also zero. Conversely, if we were given an object and told that its change in momentum is zero, then we can deduce that the net force acting on the object is also zero. Keep in mind, however, that this formula simple deals with the change in velocity. It does not mean that the object is at rest, only that its velocity remains constant.

Examples

The following examples are to test your basic understanding of Newton's First Law. For more examples that test your knowledge of all three of the laws, click .

Simple

Does the object in the following image have a net force of zero? Does it have a constant velocity?

It's easy to see that the only force on the object is acting in the +x direction, with a magnitude of 5 newtons. Therefore, the object does not have a net force of zero or a constant velocity. It will be accelerating in the +x direction.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are of each other.

Connectedness

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

The Main Idea

To be exact, the definition of the First Law of Motion is as follows:

Every body persists in its state of rest or of moving with constant speed in a constant direction, except to the extent that it is compelled to change that state by forces acting on it.

In other (and much simpler) terms, it means that an object at rest stays at rest and an object in in motion stays in motion at a constant velocity unless acted on by an unbalanced net force. It's important to keep in mind that only a difference in net force can affect the velocity of an object. The amount of change in velocity is determined by Newton's Second Law of Motion.

A Mathematical Model

Newton's first law can be stated mathematically as follows:

[math]\displaystyle{ {\vec{F_{net}} = 0 \Leftrightarrow \frac{d\vec{v}}{dt}} = 0 }[/math]

Where...

[math]\displaystyle{ \vec{F_{net}} }[/math] is the net force from the surroundings.

[math]\displaystyle{ d\vec{v} }[/math] is the change in velocity of the system.

[math]\displaystyle{ dt }[/math] is the change in time of the system

If we trace this formula from the left to the right, we can see that if the net force on an object is zero, then the change in velocity of an object is also zero. Conversely, if we were given an object and told that its change in momentum is zero, then we can deduce that the net force acting on the object is also zero. Keep in mind, however, that this formula simple deals with the change in velocity. It does not mean that the object is at rest, only that its velocity remains constant.

Examples

The following examples are to test your basic understanding of Newton's First Law. For more examples that test your knowledge of all three of the laws, click here.

Simple

Does the object in the following image have a net force of zero? Does it have a constant velocity?

It's easy to see that the only force on the object is acting in the +x direction, with a magnitude of 5 newtons. Therefore, the object does not have a net force of zero or a constant velocity. It will be accelerating in the +x direction.

Middling

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This example is slightly more difficult, but is still quite trivial. If we sum the forces in the x direction, we see that the net force is 2 newtons in the -x direction. Therefore, the object does not have a constant velocity, and will be accelerating in the -x direction.

Difficult

Does the object in the following image have a net force of zero? Does it have a constant velocity?

This final example tests your knowledge and understanding of Newton's First Law. We're able to see that the box will accelerate in the -x direction because the net force in the x direction is 5 newtons to the left. However, the box itself has a velocity of 5m/s upwards, which would indeed stay constant. This is because forces (and motion) in perpendicular directions are independent of each other.

Connectedness

The "magic trick" of ripping off a table cloth without the plates on top moving is an example of Newton's First Law. The tableware is in a state of rest, and thus want to remain in such a state.

Newton's laws of motion tie into almost everything that we see or do. The first law, in particular, explains why we suddenly lurch forward when a car suddenly stops (our bodies are in a state of motion and thus resist the sudden stop), why it's much harder to stop when ice skating than walking (there's less friction, thus less net force to decelerate), and much, much, more. The importance of Newton's first law (and by extension, the other laws of motion) is not readily apparent, but serves as a basis to explain much of our daily interactions with our surroundings.

It can also apply to things outside of our daily interactions - space, for example. Newton's first law describes why an astronaut in space will continuously float in a direction forever if they are not pulled in by an asteroid or a planet's gravitational force. There is a lack of a net force opposing the astronaut's motion (due to the fact that there is no air in space) which results in the astronaut having a constant velocity. Floating off into space is probably an astronaut's worst nightmare, a scenario that a recent movie, Gravity, explored. The entire premise of the movie (Sandra Bullock becomes untethered from her space station) relies on Newton's first law of motion.

History

While Galileo is the one credited with the idea of inertia motion, it was René Descartes, a French philosopher, who would expand upon Galileo's ideas. Descartes went on to propose three fundamental laws of nature in his book, Principles of Philosophy, the first of which stated that "each thing, as far as is in its power, always remains in the same state; and that consequently, when it is once moved, it always continues to move." Thus, while the concept of inertia is often referred to as Newton's First Law, it was first described by Galileo and then perfected by Descartes decades before Newton published his findings.

As for Newton, he first described his three laws of motion in The Mathematical Principle of Natural Philosophy, for the Principia, which was published in 1687. These laws described the relationship between an object and the forces acting upon it and laid the foundation for classical mechanics. While Newton's first law came from the work of Descartes and Galileo, his other laws are the work of himself.

Electric Field

The electric field created by a charge is present throughout space at all times, whether or not there is another charge around to feel its effects. The electric field created by a charge penetrates through matter. The field permeates the neighboring space, biding its time until it can affect anything brought into its space of interaction.

@@ Line 1,243: / Line 1,243: @@
 <div class="toccolours mw-collapsible mw-collapsed">
-====Sign of Potential Difference====
-Claimed by Tyler Quill
-<div class="mw-collapsible-content">
-*Overview
 ====Overview====
 ----