Main Page

<style>

section {

   float left;

} </style>

Welcome to the Georgia Tech Wiki for Intro Physics. This resources was created so that students can contribute and curate content to help those with limited or no access to a textbook. When reading this website, please correct any errors you may come across. If you read something that isn't clear, please consider revising it!

Looking to make a contribution?

Pick a specific topic from intro physics
Add that topic, as a link to a new page, under the appropriate category listed below by editing this page.
Copy and paste the default Template into your new page and start editing.

Please remember that this is not a textbook and you are not limited to expressing your ideas with only text and equations. Whenever possible embed: pictures, videos, diagrams, simulations, computational models (e.g. Glowscript), and whatever content you think makes learning physics easier for other students.

Source Material

All of the content added to this resource must be in the public domain or similar free resource. If you are unsure about a source, contact the original author for permission. That said, there is a surprisingly large amount of introductory physics content scattered across the web. Here is an incomplete list of intro physics resources (please update as needed).

A physics resource written by experts for an expert audience Physics Portal
A wiki book on modern physics Modern Physics Wiki
The MIT open courseware for intro physics MITOCW Wiki
An online concept map of intro physics HyperPhysics
Interactive physics simulations PhET
OpenStax algebra based intro physics textbook College Physics
The Open Source Physics project is a collection of online physics resources OSP
A resource guide compiled by the AAPT for educators ComPADRE

Organizing Categories

These are the broad, overarching categories, that we cover in two semester of introductory physics. You can add subcategories or make a new category as needed. A single topic should direct readers to a page in one of these categories.

Classes

Modeling with VPython

Theory

Notable Scientists

Properties of Matter

Contact Interactions

Momentum

Energy

Collisions

Collisions

Collisions are events that happen very frequently in our day-to-day world. In the realm of Physics, a collision is defined as any sort of process in which before and after a short time interval there is little interaction, but during that short time interval there are large interactions. When looking at collisions, it is first important to understand two very important principles: the Momentum Principle and the Energy Principle. Both principles serve use when talking of collisions because they provide a way in which to analyze these collisions. Collisions themselves can be categorized into 3 main different types: elastic collisions, inelastic collisions, maximally inelastic collisions. All 3 collisions will get touched on in more detail further on.

Elastic Collisions

A collision is deemed "elastic" when the internal energy of the objects in the system does not change (in other words, change in internal energy equals 0). Because in an elastic collision no kinetic energy is converted over to internal energy, in any elastic collision Kfinal always equals Kinitial.

Inelastic Collisions

A collision is said to be "inelastic" when it is not elastic; therefore, an inelastic collision is an interaction in which some change in internal energy occurs between the colliding objects (in other words, change in internal energy does not equal 0). Examples of such changes that occur between colliding objects include, but are not limited to, things like they get hot, or they vibrate/rotate, or they deform. Because some of the kinetic energy is converted to internal energy during an inelastic collision, Kfinal does not equal Kinitial. There are a few characteristics that one can search for when identifying inelasticity. These indications include things such as:

Objects stick together after the collision
An object is in an excited state after the collision
An object becomes deformed after the collision
The objects become hotter after the collision
There exists more vibration or rotation after the collision

Maximally Inelastic Collision

Maximally inelastic collisions, also known as "sticking collisions", are the most extreme kinds of inelastic collisions. Just as its secondary name implies, a maximally inelastic collision is one in which the colliding objects stick together creating maximum dissipation. This does not automatically mean that the colliding objects stop dead because the law of conservation of momentum. In a maximally inelastic collision, the remaining kinetic energy is present only because total momentum can't change and must be conserved.

Head-on Collision of Equal Masses

The easiest way to understand this phenomenon is to look at it through an example. In this case, we can analyze it through the common game of billiards. Taking the two, equally massed billiard balls as the system, we can neglect the small frictional force exerted on the balls by the billiard table. The Momentum Principle states that in this head-on collision of billiard balls the total final momentum in the x direction must equal the total initial momentum. However, this alone does not give us the knowledge to know how the momentum will be divided up between the two balls. Considering the law of conservation of energy, we can more accurately depict what will happen. This will also allow for one to identify what kind of collision occurs (elastic, inelastic, or maximally inelastic). It is important to know that head-on collisions of equal masses do not have a definite type of collision associated with it.

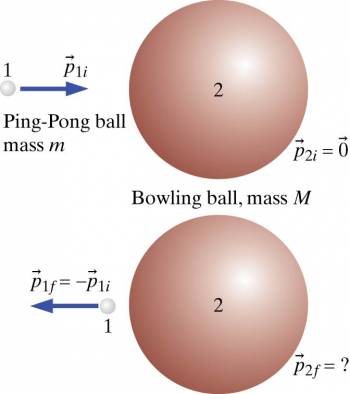
Head-on Collision of Unequal Masses

Just as with head-on collisions of equal masses, it is easy to understand head-on collisions of unequal masses by viewing it through an example. Let's take for example two balls of unequal masses like a ping-pong ball and a bowling ball. For the purpose of this example (so as to allow for no friction and no other significant external forces), let's imagine these objects collide in outer space inside an orbiting spacecraft. If there were to be a collision between the two, what would one expect to happen? One could expect to see the ping-pong ball collide with the bowling ball and bounce straight back with a very small change of speed. What one might not expect as much is that the bowling ball also moves, just very slowly. Again, this can all be explained through the conservation of momentum and the conservation of energy.

Frame of Reference

In the world of Physics, a frame of reference is the perspective from which a system is observed. It can be stationary or sometimes it can even be moving at a constant velocity. In some rare cases, the frame of reference moves at an nonconstant velocity and is deemed "noninertial" meaning the basic laws of physics do not apply. Continuing with the trend of examples, pretend you are at a train station observing trains as they pass by. From your stationary frame of reference, you observe that the passenger on the train is moving at the same velocity as the train. However, from a moving frame of reference, say from the eyes of the train conductor, he would view the train passengers as "anchored" to the train.

Scattering: Collisions in 2D and 3D

Experiments that involve scattering are often used to study the structure and behavior of atoms, nuclei, as well as of other small particles. In an experiment like such, a beam of particles collides with other particles. If it is an atomic or nuclear collision, we are unable to observe the curving trajectories inside the tiny region of interaction. Instead, we can only truly observe the trajectories before and after the collision. This is only possible because the particles are at a farther distance apart and have a very weak mutual interaction; this essentially means that the particles are moving almost in a straight line. A good example which demonstrates scattering is the collision between an alpha particle (the nucleus of a helium atom) and the nucleus of a gold atom. One will understand this phenomenon more in depth after first understanding the Rutherford Experiment which will get touched on later.

Rutherford Experiment and Atomic Collisions

In England in 1911, a famous experiment was performed by a group of scientists led by Mr. Ernest Rutherford. This experiment, later known as "The Rutherford Experiment", was a tremendous breakthrough for its time because it led to the discovery of the nucleus inside the atom. Rutherford's experiment involved the scattering of a high-speed alpha particle (now known as a helium nuclei - 2 protons and 2 neutrons) as it was shot at a thin gold foil (consisting of a nuclei with 79 protons and 118 neutrons). In the experiment, Rutherford and his team discovered that the velocity of the alpha particles was not high enough to allow the particles to make actual contact with the gold nucleus. Although they never actually made contact, it is still deemed a collision because there exists a sizable force between the alpha particle and the gold nucleus over a very short period of time. In conclusion, we say the alpha particle is "scattered" by its interaction with the nucleus of a gold atom and experiments like such are called "scattering" experiments.

Coefficient of Restitution

The coefficient of restitution is a measure of the elasticity in a collision. It is the ratio of the differences in velocities before and after the collision. The coefficient is evaluated by taking the difference in the velocities of the colliding objects after the collision and dividing by the difference in the velocities of the colliding objects before the collision.

All of the following information was collected from the Matter and Interactions 4th Edition physics textbook. The book is cited as follows...

Chabay, Ruth W., and Bruce A. Sherwood. "Chapter 10: Collisions." Matter & Interactions. Fourth Edition ed. Wiley, 2015. 383-409. Print.

Fields

Radiation

Sound

Waves

Real Life Applications of Electromagnetic Principles

Optics

Resources

Commonly used wiki commands Wiki Cheatsheet
A guide to representing equations in math mode Wiki Math Mode
A page to keep track of all the physics Constants
A page for review of Vectors and vector operations

Physics 1

Week 1

Help with VPython

Vectors and Units

Vectors

Interactions

Velocity and Momentum

Week 2

Momentum and the Momentum Principle

Momentum Principle

Iterative Prediction with a Constant Force

Week 3

Analytical Prediction with a Constant Force

Iterative Prediction with a Varying Force

Week 4

Fundamental Interactions

Week 5

Conservation of Momentum

Conservation of Momentum

Properties of Solids

Week 6

Identifying Forces

Curving Motion

Week 7

Energy Principle

The Energy Principle

Week 8

Work by Non-Constant Forces

Potential Energy

Week 9

Multiparticle Systems

Week 10

Choice of System

Forms of Energy

Thermal Energy

Week 11

Different Models of a System

Models of Friction